Forza di trascinamento: definizione, formula, tipi ed esempi

Início » Ciência » Física » Forza di trascinamento: definizione, formula, tipi ed esempi

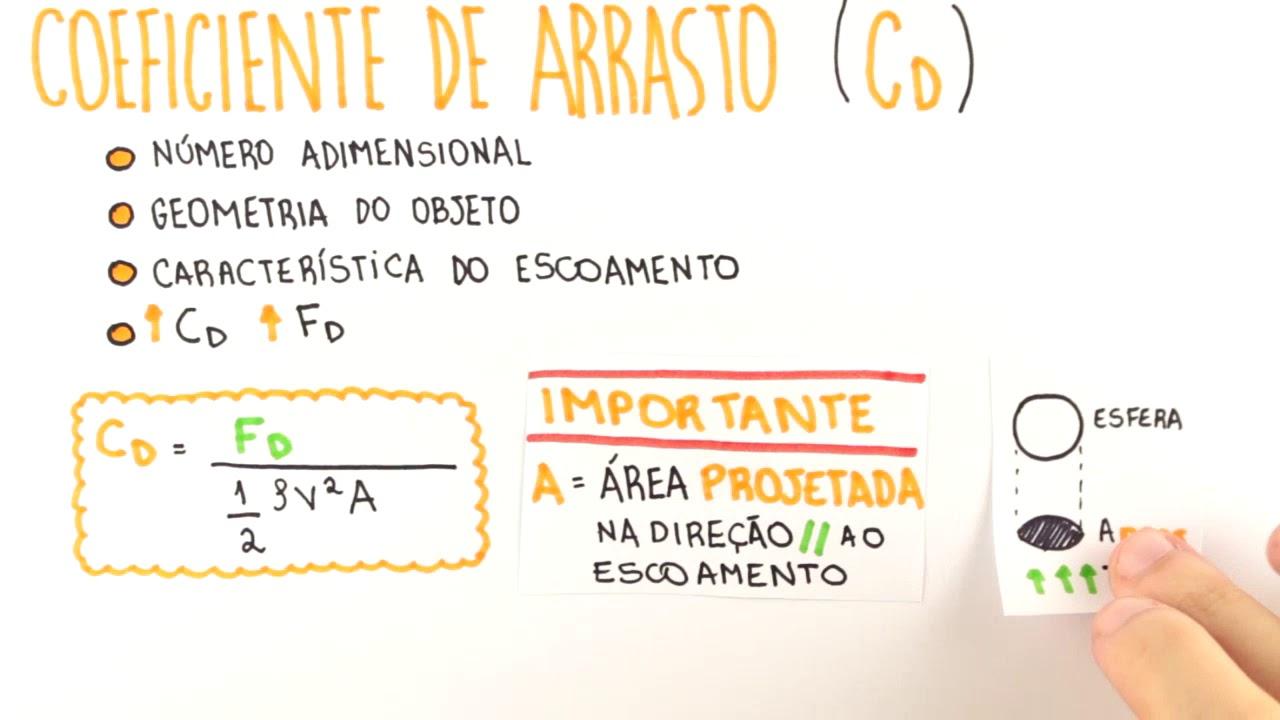
Se ti sei mai chiesto perché un’auto disegnata in galleria del vento consumi meno o come facciano i paracadutisti a rallentare in modo così efficace, la risposta sta tutta nella forza di trascinamento. È la forza di resistenza che un fluido, sia esso aria o acqua, oppone al moto di un corpo che lo attraversa, e cresce con la velocità, la forma, l’area esposta e la densità del fluido.

Dal punto di vista pratico, la forza di trascinamento spiega fenomeni che vanno dalle prestazioni degli atleti in piscina alle scelte progettuali di aerei, auto e imbarcazioni. In fisica e in ingegneria si calcola con una formula semplice ma potentissima, che mostra come il trascinamento sia proporzionale al quadrato della velocità e dipenda da un coefficiente adimensionale legato alla forma dell’oggetto. Nei paragrafi che seguono trovi definizioni chiare, formule, esempi svolti passo passo e i diversi tipi di drag che contano davvero.

Che cos’è la forza di trascinamento

Con forza di trascinamento si indica la resistenza che un fluido esercita su un corpo in moto al suo interno. In generale, questa forza ha verso opposto al moto e modulo che cresce quando aumentano area esposta, densità del fluido, coefficiente di trascinamento e velocità del corpo.

In parole semplici: se presenti al fluido un’area più grande o una forma poco aerodinamica, il fluido opporrà più resistenza; se ti muovi in aria rarefatta avrai meno drag rispetto all’aria densa al livello del mare; se raddoppi la velocità, la forza non raddoppia: quadruplica.

• Area di contatto efficace: maggiore è l’area perpendicolare alla velocità, maggiore sarà la resistenza.
• Coefficiente di trascinamento (C): dipende dalla forma; profili aerodinamici hanno C basso, corpi tozzi C alto.
• Densità del fluido (ρ): un fluido più denso (per esempio l’acqua rispetto all’aria) genera un drag più grande a parità di condizioni.
• Velocità (v): il drag con contributo quadratico cresce come v²; a velocità raddoppiata, la forza diventa quattro volte maggiore.

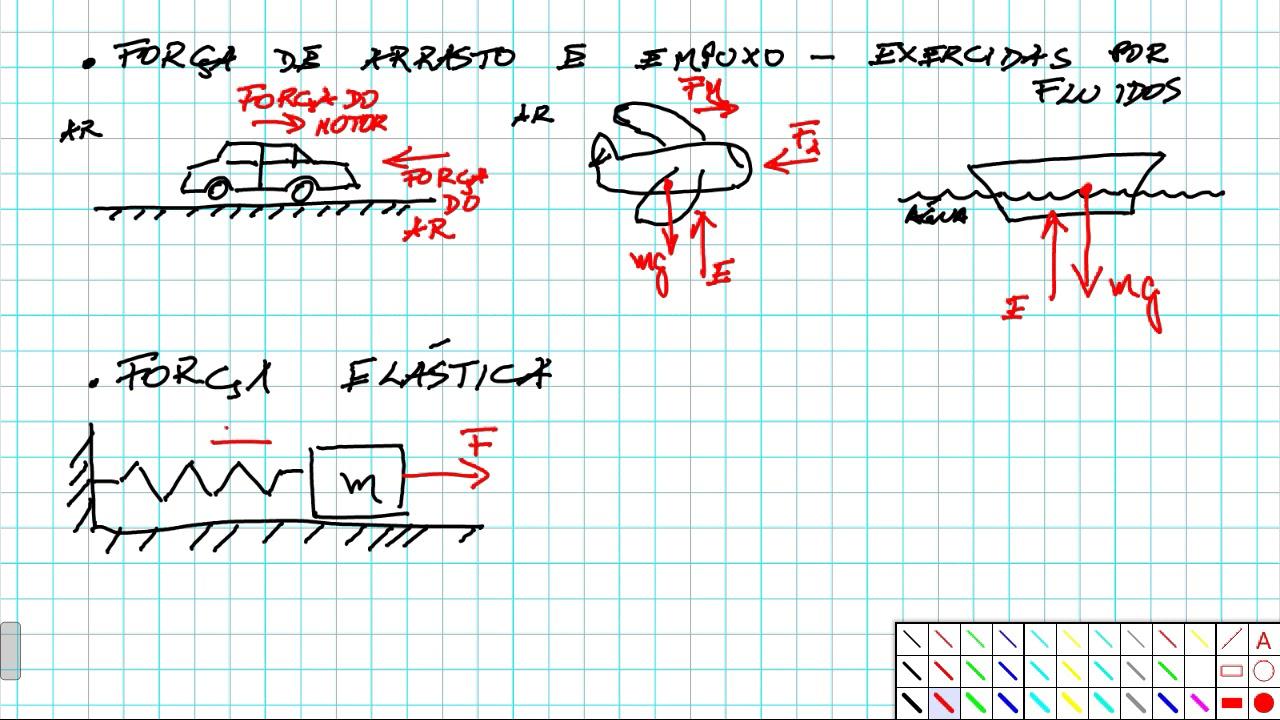
Formula della forza di trascinamento

La relazione più usata per il drag con contributo quadratico è: D = (1/2) · C · ρ · A · v². Questa espressione sintetizza l’effetto combinato di forma, ambiente e velocità sul valore della forza.

• D: modulo della forza di trascinamento, in Newton (N).
• C: coefficiente di trascinamento (adimensionale), tipicamente compreso tra ~0,4 e 1 per molte geometrie comuni; ad esempio, una sfera liscia spesso si assume con C ≈ 0,5.
• ρ: densità del fluido, in kg/m³.
• A: area della sezione retta efficace, cioè l’area proiettata perpendicolare alla velocità, in m².
• v: velocità relativa del corpo rispetto al fluido, in m/s.

Questa formula è largamente valida quando domina la componente quadratica del drag, che è la più importante a velocità medio-alte; in regimi molto lenti può emergere anche una dipendenza più lineare dalla velocità, ma nei casi pratici trattati qui il termine in v² è quello che conta.

Come si calcola il trascinamento: procedura ed esempio

Per calcolare il drag si identificano C, ρ, A e v, quindi si sostituiscono i valori nella formula. Spesso l’unico passaggio preliminare è determinare l’area A in funzione delle dimensioni del corpo. Una volta impostata l’area, il resto è un’applicazione diretta.

Esempio 1 – sfera nell’aria: Considera un corpo sferico con C = 0,5, area efficace A = 2 · 10⁻² m², che si muove in aria con v = 30 m/s. Assumi ρ_aria = 1 kg/m³. Il modulo della forza è:

D = (1/2) · C · ρ · A · v² = 0,5 · 0,5 · 1 · (2 · 10⁻²) · (30)²

Svolgendo i conti otteniamo D = 4,5 N. Il risultato mostra bene l’effetto della velocità al quadrato: se la velocità raddoppiasse, il drag quadruplicherebbe.

Esempio 2 – missile a bassa quota: Supponi un missile con coefficiente C = 0,75, densità dell’aria ρ = 1,2 kg/m³, velocità v = 250 m/s e diametro d = 0,53 m. L’area efficace è il cerchio frontale: A = π(d/2)² ≈ π · 0,265² ≈ 0,2209 m². Applicando la formula si ottiene D ≈ 6,2 kN, valore coerente con un regime ad alta velocità in aria densa.

Linee di flusso: laminare e turbolento

Per capire come si genera il drag è utile visualizzare le linee di flusso, cioè le traiettorie seguite idealmente dalle particelle del fluido. Quando queste linee sono ben ordinate e parallele tra loro, il flusso è laminare e la resistenza è minore; al contrario, con scie e vortici caotici il flusso diventa turbolento e il drag cresce.

In regime laminare le particelle scorrono con ordine, gli strati del fluido si sfiorano con poca mescolanza e la superficie liscia del corpo aiuta a ridurre la resistenza. A basse velocità e con profili ben sagomati è più facile rimanere in questa condizione.

Quando la velocità aumenta o la forma è poco streamlinata, dietro al corpo si forma una scia turbolenta con pressione più bassa rispetto alla zona frontale: la differenza di pressione genera una forza netta opposta al moto, aumentando il drag. Questo comportamento spiega le scelte di design nelle auto sportive e negli aerei.

La natura di queste linee è legata anche alla viscosità del fluido: superfici più ruvide “trascinano” strati adiacenti e favoriscono turbolenza. È il motivo per cui tute da nuoto e telai di bici ad alte prestazioni puntano a finiture molto lisce.

Tipi di trascinamento: superficie, forma, onda

La forza totale di drag può essere scomposta in contributi distinti. In pratica si parla di trascinamento di superficie, di forma e d’onda, ciascuno dominato da meccanismi diversi e influenzato dalla geometria del corpo e dal regime di moto.

Drag di superficie: nasce dal contatto diretto tra fluido e superficie del corpo ed è legato all’attrito viscoso nello strato limite. Maggiore rugosità significa più interazione e quindi più resistenza. Da qui l’uso di superfici lisce in nuoto competitivo o sull’ala di un aereo.

Drag di forma: è associato alle differenze di pressione tra la parte anteriore e quella posteriore dell’oggetto, spesso a causa della scia turbolenta che si forma dietro. Una scocca aerodinamica riduce l’area perpendicolare al flusso e attenua la separazione dello strato limite, limitando le perdite.

Drag d’onda: compare quando il corpo si muove vicino alla superficie libera di un fluido praticamente incomprimibile (come l’acqua), generando onde che “rubano” energia al moto. È evidente per navi e nuotatori che nuotano a pelo d’acqua; se il corpo è completamente immerso e lontano dalla superficie, questo contributo si riduce drasticamente.

Velocità terminale e bilancio delle forze

Un oggetto in caduta in aria accelera finché il drag non si eguaglia al suo peso. In quel momento la forza risultante si annulla e la velocità si stabilizza a un valore costante detto velocità terminale. Questo fenomeno è cruciale per comprendere i salti con il paracadute e il moto di gocce di pioggia.

Se il drag è quadratico, e con F_g = m g, la velocità terminale è data da: v_t = √[ 2 F_g / (C ρ A) ]. Qui A è l’area proiettata e C il coefficiente alla velocità in questione. Il risultato mostra che v_t cresce con la radice della massa e diminuisce con C, ρ e A.

Esempio – goccia di pioggia: Considera una goccia sferica di raggio R = 1,5 mm, con C = 0,60, ρ_acqua = 1000 kg/m³, ρ_aria = 1,2 kg/m³. La massa è m = (4/3)πR³ρ_acqua e l’area proiettata A = πR². Sostituendo nella formula si ottiene: v_t = √[ (8/3) · R · ρ_acqua · g / (C · ρ_aria) ] ≈ 7,4 m/s. Valore assolutamente realistico per gocce di qualche millimetro di diametro.

Esercizi ed esempi svolti

Per fissare i concetti, vediamo alcuni casi tipici che compaiono spesso negli esercizi di fisica di base e nelle applicazioni ingegneristiche. Ogni esempio mette in luce una diversa dipendenza del drag.

Esercizio 1 – confronto tra posizioni di un paracadutista: Un atleta scende a v_t1 = 160 km/h in posizione “a candela” (più area esposta) e a v_t2 = 310 km/h in posizione “head down” (meno area). Supponendo stesso C e stessa ρ per le due pose, la relazione dalla formula è v_t ∝ 1/√A. Dunque: A_candela / A_{head down} = (v_t2/v_t1)² = (310/160)² ≈ 3,75. La posizione raccolta riduce in modo drastico l’area e quindi aumenta molto la velocità terminale.

Esercizio 2 – sfera piccola nell’aria: Un oggetto sferico con C = 0,5, area A = 7,0 cm² = 7,0 · 10⁻⁴ m², si muove in aria a v = 10,0 m/s, con ρ ≈ 1,0 kg/m³. Applicando la formula: D = 0,5 · 0,5 · 1,0 · (7,0 · 10⁻⁴) · (10,0)² = 0,0175 N. Questo ordine di grandezza è tipico di oggetti molto piccoli e lenti.

Esercizio 3 – effetto della massa sulla velocità terminale: Due corpi geometricamente identici (stessa forma e dimensioni) cadono in aria; il secondo ha massa quattro volte quella del primo. Con v_t = √[ 2 m g / (C ρ A) ] e A, C, ρ invariati, segue v′/v = √(m′/m) = √4 = 2. In altri termini, raddoppia la velocità terminale, non quadruplica: la dipendenza è radice quadrata.

Esercizio 4 – ruolo delle linee di flusso: In regime laminare (linee parallele e ordinatissime) il drag è minore rispetto al regime turbolento (scia caotica e vortici). È per questo che superfici lisce e forme affusolate abbassano C, mentre angoli vivi e superfici ruvide lo aumentano, con impatto diretto sulla resistenza e sui consumi di energia.

Unità di misura, stime tipiche e note di progetto

Quando lavori con il drag, tieni a mente le unità: N per la forza, kg/m³ per la densità, m² per l’area, m/s per la velocità. I coefficienti C si estraggono da tabelle o prove sperimentali; per molte geometrie comuni si muovono tra 0,4 e 1,0, ma profilature ottimizzate possono scendere molto di più.

In automotive e aeronautica si utilizzano gallerie del vento per misurare C e studiare la scia: ridurre la pressione dietro il veicolo migliora stabilità e consumi. All’opposto, i paracadute cercano deliberatamente grande area e alto C per massimizzare il drag e ottenere velocità terminali basse e sicure.

Nel nuoto e nella vela, il drag di superficie è fondamentale: una riduzione della rugosità della pelle o della carena comporta perdite minori, con vantaggi immediati in gara. Nelle navi che navigano a pelo d’acqua il drag d’onda può dominare: la formazione di onde di prua assorbe energia e limita la velocità economica.

Infine, ricorda che in aria rarefatta (alta quota) il parametro ρ cala: a parità di forma e velocità, il drag diminuisce. Questo spiega perché aerei e proiettili ad alta quota incontrano meno resistenza, ma anche perché l’aerodinamica resta critica nelle fasi di decollo e atterraggio vicino al suolo.

Guardando l’insieme, la forza di trascinamento è il ponte fra teoria dei fluidi e applicazioni reali: dipende dalla forma, dalla densità del fluido, dall’area esposta e cresce con il quadrato della velocità; le linee di flusso spiegano la differenza fra flusso laminare e turbolento, mentre i tre contributi principali (superficie, forma, onda) chiariscono dove intervenire per ridurre o aumentare la resistenza, che sia per rendere un’auto più efficiente o per far atterrare dolcemente un paracadutista.