Energia interna: significato, formule e applicazioni chiave

Início » Ciência » Física » Energia interna: significato, formule e applicazioni chiave

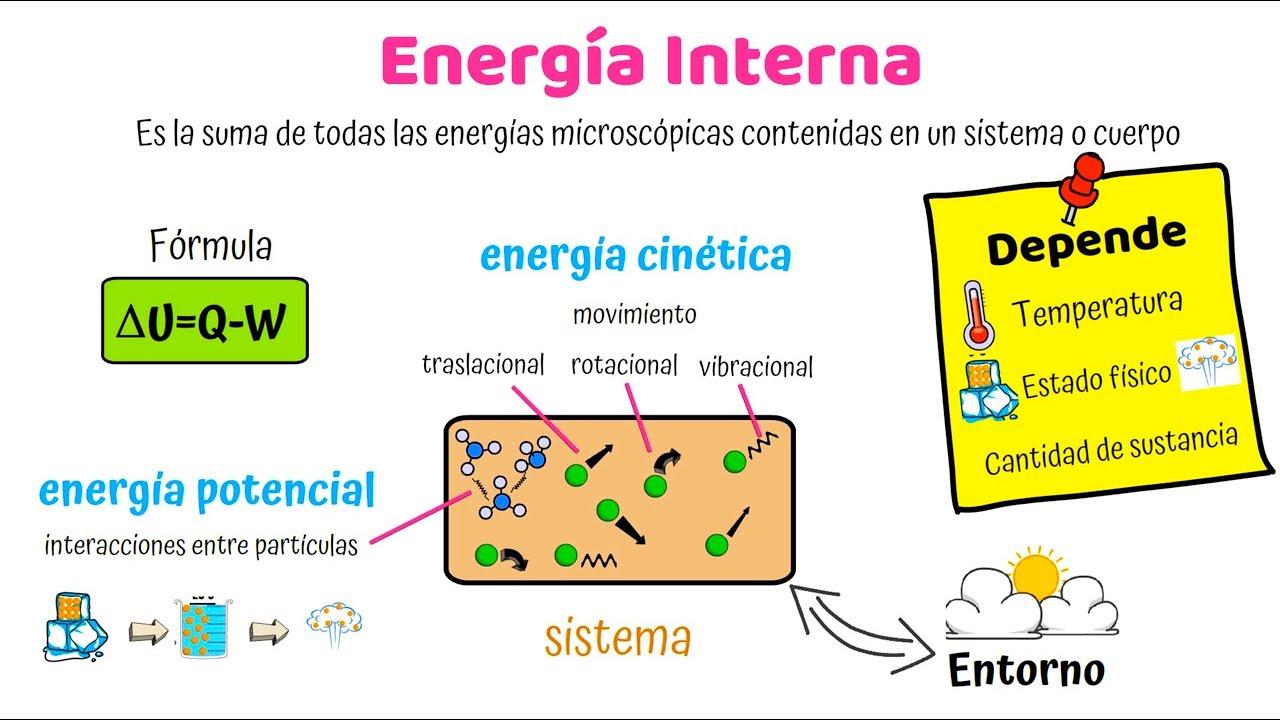
L’energia interna è il “conto in banca” microscopico dell’energia in un sistema: descrive tutto ciò che accade a livello di molecole, atomi ed elettroni, indipendentemente da come il corpo si muova o da dove si trovi nello spazio. In altre parole, non include l’energia dovuta al moto complessivo del sistema né l’energia potenziale associata a campi esterni rispetto al riferimento usato.

Per capire come si modifica e come si misura, il primo principio della termodinamica e distinguere bene tra le varie forme con cui l’energia “vive” dentro la materia: contributi cinetici (traslazione, rotazione, vibrazione), contributi elettronici, e perfino la parte “irriducibile” di energia di punto zero che non scompare neppure a 0 K.

Che cos’è, davvero, l’energia interna

Somma di tutte le energie cinetiche e potenziali delle entità microscopiche del sistema. Questo significa che U raccoglie: energia di traslazione, rotazione e vibrazione delle molecole; energia associata agli elettroni; energia termica; ed energia di punto zero. Restano escluse, invece, l’energia cinetica dovuta al moto del sistema nel suo insieme e l’energia potenziale dovuta all’interazione con forze esterne (per esempio un campo gravitazionale esterno fissato come riferimento).

Possiamo pensarla come una somma estesa a tutte le particelle: U = Σ(Energia cinetica i-esima + Energia potenziale i-esima). Non serve scrivere simboli complessi per cogliere l’idea: si sommano i contributi interni, e basta.

Una caratteristica cruciale è che funzione di stato: la sua variazione dipende solo dallo stato iniziale e da quello finale, non dal percorso seguito. Questo è il motivo per cui in analisi dei processi ci interessa soprattutto ΔU tra due stati A e B, con ΔU = U_B − U_A, senza inseguire cosa accade passo per passo.

Dal punto di vista dimensionale e operativo, grandezza estensiva (cresce con la quantità di materia). Per rendere i valori confrontabili tra sistemi diversi, si introducono quantità specifiche: u = U/m (energia interna massica) e u_mol = U/n (energia interna molare), dove m è la massa e n le moli. Queste versioni sono grandezze intensive utilissime in ingegneria e chimica fisica.

In SI, joule (J) è l’unità di misura di riferimento per U. Questo vale tanto per la grandezza estensiva quanto per le corrispondenti grandezze specifiche, opportunamente normalizzate per massa o per moli.

Contributi principali che compongono U (vista “a spicchi”):

• Energia cinetica traslazionale: moto caotico delle particelle con urti continui tra loro e con le pareti.
• Energia cinetica rotazionale: rotazione delle molecole attorno al centro di massa.
• Energia cinetica vibrazionale: vibrazioni degli atomi all’interno delle molecole.
• Energia elettronica: stati energetici degli elettroni legati.
• Energia di punto zero: il “minimo non nullo” a 0 K dovuto alla meccanica quantistica.

Nota pratica: per molecole monoatomiche (He, Ar, Ne…), il contributo dominante è la traslazione; per biatomiche (come H₂) si aggiungono rotazione e vibrazione; per molecole più complesse, le vibrazioni possibili sono molte di più.

Primo principio della termodinamica e convenzioni di segno

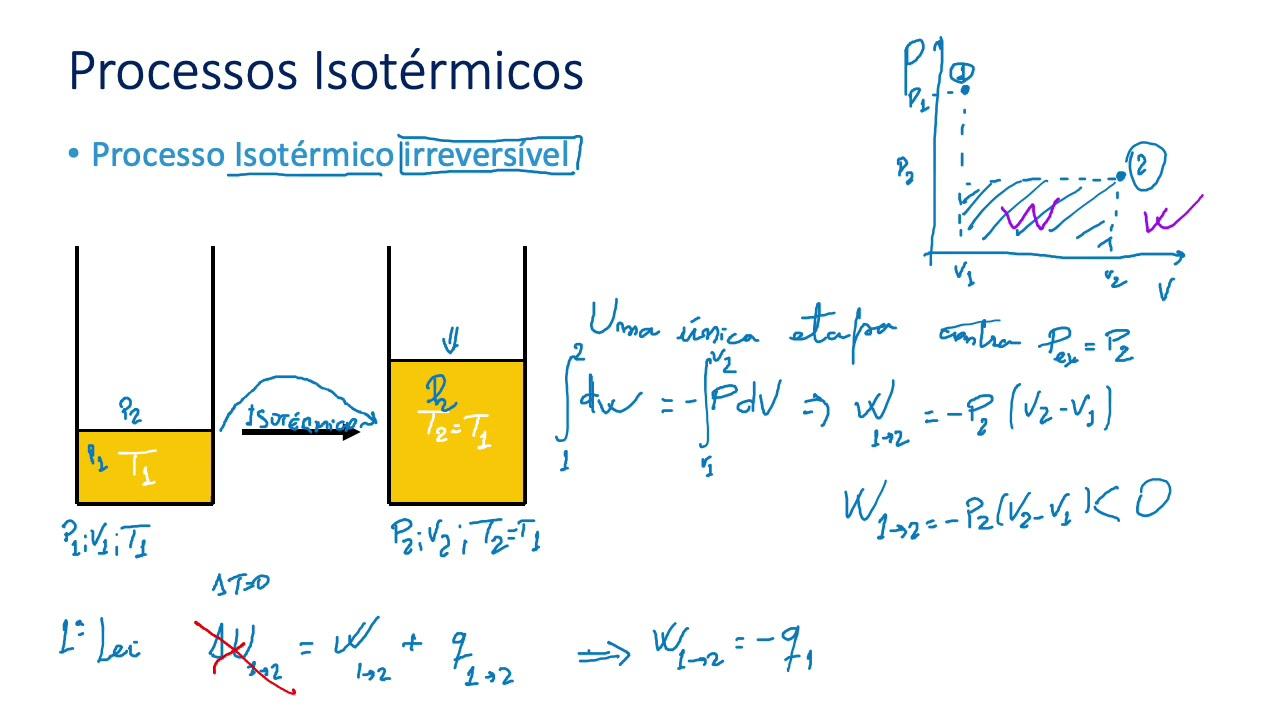
Il primo principio, nella forma più familiare, ci dice che ΔU = Q − L: ΔU = Q − L. Qui L è il lavoro svolto dal sistema sull’ambiente (positivo se il sistema lavora verso l’esterno). Se si preferisce la convenzione opposta per il lavoro (positivo se fatto sull’interno), la formula equivalente diventa ΔU = Q + L. Cambia il segno di L, non la fisica.

In un sistema isolato, assenza di scambi di calore e lavoro implica ΔU = 0: l’energia interna resta costante. Questo è il collegamento diretto con la più generale legge di conservazione dell’energia.

Per processi particolari emergono risultati rapidi da ricordare: se il sistema riceve calore (Q > 0) senza compiere lavoro, U aumenta; se compie lavoro a volume variabile senza ricevere calore (processo adiabatico), U diminuisce. Il dettaglio chiave è che Q e L dipendono dal percorso, mentre ΔU no: è qui che si vede la natura di funzione di stato di U.

Dal punto di vista differenziale, in forma generale e per trasformazioni quasi-statiche, dU = T dS − p dV + μ · dn (con μ vettore dei potenziali chimici e n vettore delle quantità di sostanza). Questa è la “mappa” che lega U alle variabili fondamentali per sistemi semplici o reagenti.

Variabili naturali di U: entropia, volume e composizione

Per molti sistemi non reagenti con solo lavoro di volume, funzione di S e V: U = U(S, V). Quando la composizione cambia (reazioni chimiche, mescolamenti), occorre includere anche i quantitativi di sostanza n delle singole specie: U = U(S, V, n). In questa cornice, il differenziale precedente dU = T dS − p dV + μ · dn esprime in modo elegante come variano temperatura T, pressione p e potenziali chimici μ rispetto alle sue variabili “naturali”.

Forme intensive sono comode quanto si ragiona per unità di massa. entropia specifica s, densità ρ, e masse molari raccolte nel vettore M, si può scrivere un differenziale per l’energia interna specifica u che coinvolga 1/ρ e 1/M come variabili intensive accoppiate; la logica resta la stessa: pressione e temperatura restano moltiplicatori coniugati alle rispettive variabili.

Quando il processo è finito tra due stati vicini e quasi-statico, si può passare a incrementi finiti coerenti con i lavori scambiati: per esempio, ΔU = TΔS − pΔV + μ · Δn, utile nelle analisi di bilancio energetico e di equilibrio chimico.

Gas ideali: U dipende solo dalla temperatura

Nel modello di gas ideale a composizione fissa, assenza di interazioni intermolecolari (energia potenziale interna assunta nulla) e l’energia interna coincide con la somma dell’energia cinetica traslazionale delle molecole. Questo porta a un risultato potentissimo: dipende solo dalla temperatura.

La relazione operativa più usata è ΔU = n c_V ΔT, dove c_V è il calore specifico a volume costante (molar o massico). In molti casi c_V si può stimare con il teorema di equipartizione della meccanica statistica classica: ogni grado di libertà quadratico contribuisce per (1/2)k_BT di energia media per molecola. Se indichiamo con f i gradi di libertà effettivi, (f/2) k_B T è l’energia cinetica media per molecola.

Moltiplicando l’energia media per il numero di molecole N (oppure, equivalentemente, usando n moli e la costante dei gas R = N_A k_B), si ottiene la forma compatta: U = (f/2) n R T. Per un gas monoatomico ideale (traslazione in tre dimensioni), tipicamente f = 3 e si ha U = (3/2) n R T; per specie biatomiche si aggiungono i contributi rotazionali, e a temperatura abbastanza alta anche quelli vibrazionali.

Con l’equazione di stato dei gas perfetti pV = nRT, si collegano in modo lineare pressione, volume e temperatura, ma si tenga presente che, per il gas ideale, U non dipende da p né da V autonomamente: è la temperatura a pilotare tutto.

Gas reali, liquidi e solidi: che cosa cambia

Nel mondo reale le molecole si attraggono e si respingono: forze intermolecolari rendono non trascurabile l’energia potenziale interna. In un gas reale, il contributo potenziale è spesso piccolo ma non nullo; nei liquidi e nei solidi diventa dominante nel determinare la struttura e la coesione.

Per convenzione energetica, energia potenziale di legame risulta spesso negativa rispetto a uno zero fissato a molecole “infinito lontane”. Così, un solido fortemente legato ha una parte potenziale molto importante (in modulo), mentre la parte cinetica termica tende a “disordinare” e a separare. Non è strano quindi che, a seconda della sostanza e della temperatura, il bilancio complessivo dell’energia interna sia guidato da quale contributo prevalga.

Ne deriva un quadro intuitivo ma utile: nei gas l’energia cinetica domina e l’effetto potenziale è modesto; nei solidi i legami sono robusti e l’energia potenziale (negativa rispetto allo zero di riferimento) pesa di più; i liquidi stanno nel mezzo, con contributi di ordine simile e una libertà di movimento inferiore a quella dei gas ma maggiore rispetto ai solidi.

Quando si calcola U per un gas reale, bisogna quindi sommare entrambe le parti: U = K + E_pot. Questa distinzione è particolarmente importante vicino ai cambi di fase e per miscele reali, dove compaiono termini di interazione tra specie diverse.

Relazioni con altri potenziali termodinamici

U non è sola: si collega a entalpia, energia libera di Helmholtz ed energia libera di Gibbs con relazioni lineari che coinvolgono pV e TS. Le più usate sono:

• U = H − pV (con H entalpia)
• U = A + TS (con A energia libera di Helmholtz)
• U = G − pV + TS (con G energia libera di Gibbs)

Per un gas ideale, usando pV = nRT, si ottiene ad esempio U = H − nRT. Queste identità sono preziose per passare da un potenziale all’altro a seconda delle variabili “comode” per il problema (T, p, V, S, n) e per interpretare i termini pV e TS come parti non disponibili o “anergia” in certe letture ingegneristiche.

Meccanica statistica e funzione di partizione

Nel formalismo canonico, la relazione sintetica è: U = − ∂ ln Z / ∂β, dove Z è la funzione di partizione canonica e β = 1/(k_BT). Con questa porta d’accesso, l’energia interna diventa un ponte tra il mondo microscopico (spettri energetici, stati accessibili) e le grandezze termodinamiche macroscopiche.

Il vantaggio concettuale è enorme: dalla struttura microscopica si risale a U e, con passaggi standard, a tutte le altre proprietà termodinamiche. È il senso profondo per cui l’energia interna “sa” della distribuzione di popolazione degli stati e del ruolo della temperatura come parametro di controllo.

Trasformazioni tipiche: isocora, adiabatica, isoentropica

Nelle trasformazioni isocore (V costante), il lavoro di volume è nullo e, per un sistema semplice, il calore scambiato coincide con la variazione di energia interna: Q = ΔU. Per questo motivo c_V è così centrale: collega direttamente temperatura ed energia interna.

In una trasformazione adiabatica (Q = 0), se il sistema compie lavoro verso l’esterno, ΔU è negativa. Nei processi adiabatici reversibili e per gas ideali si ritrovano le ben note leggi pV^γ = costante e relazioni T–V, a conferma che temperatura ed energia interna decrescono quando il sistema si espande lavorando.

Per trasformazioni isoentropiche (S costante), vale dU = −p dV + μ · dn: a composizione fissa, il cambiamento di U è legato al solo lavoro di volume. In casi speciali, isocori e isoentropici insieme, la variazione di U può coincidere con la “parte disponibile” rispetto ad altri potenziali, ma sono scenari ideali che si usano per fissare idee e limiti teorici.

Energia interna e interpretazione chimica

Quando avviene una reazione, si scambiano “pacchetti” tra energia potenziale di legame ed energia cinetica. Se i prodotti possiedono complessivamente legami più stabili (energia potenziale minore) rispetto ai reagenti, l’eccesso si riversa in energia cinetica delle particelle e quindi in calore ceduto all’ambiente: è il caso delle reazioni esotermiche.

Al contrario, quando servono legami più “costosi” per costruire i prodotti, il sistema assorbe calore dall’esterno che va a incrementare l’energia potenziale chimica interna: parliamo di reazioni endotermiche. In entrambi i casi, la variazione di energia interna riflette questo bilancio tra stati iniziali e finali, indipendentemente dalla via di reazione.

Una frase utile da ricordare è che energia dei legami rappresenta l’energia potenziale chimica di un insieme di molecole (intra- e intermolecolari). Da qui discende l’idea pratica che l’energia interna in chimica sia “termica + chimica”, unendo la parte cinetica e quella potenziale di legame.

Esempi numerici e grandezze specifiche

Per un gas monoatomico ideale, ogni molecola ha solo traslazione (rotazioni e vibrazioni non contribuiscono alla temperatura ordinaria). In questo caso si ha U = (3/2) nRT. Per un gas biatomico, entrano in gioco i gradi rotazionali e, a temperatura abbastanza alta, le vibrazioni: il valore effettivo di f cresce e con esso la pendenza di U rispetto a T.

È spesso comodo lavorare con quantità specifiche. L’energia interna massica u = U/m permette di confrontare materiali diversi a parità di massa; l’energia interna molare u_mol = U/n consente confronti per moli ed è naturale in chimica. Anche il calore specifico si usa in forma massica (J kg⁻¹ K⁻¹) o molare (J mol⁻¹ K⁻¹) in funzione dell’applicazione.

In tutti i casi, capacità termica × ΔT è il prodotto che spesso guida la valutazione di ΔU in condizioni opportune (isocore) o, per generalità e precisione, si ricorre all’analisi dU = T dS − p dV + μ · dn quando servono processi con reazioni o con scambi di materia.

Come leggere i segni in pratica

Con la convenzione ΔU = Q − L (lavoro positivo se fatto dal sistema), casi guida aiutano a non sbagliare:

• Se il sistema assorbe calore e non fa lavoro: ΔU > 0 (Q > 0, L = 0).
• Se il sistema compie lavoro senza scambiare calore (adiabatico): ΔU < 0 (Q = 0, L > 0).
• Se l’ambiente compie lavoro sul sistema (L < 0) e contemporaneamente il sistema riceve calore (Q > 0): ΔU aumenta in misura Q − L.

Se si usa la convenzione alternativa ΔU = Q + L (con L positivo se il lavoro è fatto sull’interno), gli esiti fisici coincidono; è solo questione di coerenza nel tenere i segni lungo i calcoli.

Nota su entropia, temperatura e interpretazione statistica

Dal differenziale dU = T dS − p dV + μ · dn emerge che temperatura è il moltiplicatore coniugato dell’entropia. A volume e composizione fissi, un piccolo aumento di entropia si riflette in un aumento proporzionale di U via T. Al contrario, a entropia costante, la variazione di U è legata al lavoro di volume (e alla composizione quando variabile): è un modo essenziale di leggere i processi reversibili e di collegare la termodinamica classica alla statistica.

La chiave statistica, ricordiamolo, fa riferimento alla funzione di partizione Z e alla variabile β = 1/(k_BT): U = − ∂ ln Z / ∂β. In pratica, conoscendo gli stati energetici accessibili e come si popolano al variare di T, si ricostruisce l’energia interna e poi, per via termodinamica, molte altre proprietà.

Collegamenti utili con esperienze didattiche

Nei corsi introduttivi si insiste spesso su tre esperimenti mentali: riscaldamento isocoro (il gas assorbe calore e la sua U aumenta di n c_V ΔT), espansione adiabatica (il gas lavora verso l’esterno e la sua U diminuisce), e compressione adiabatica (l’ambiente fa lavoro sul gas e U aumenta). Questi casi, pur semplici, riassumono bene il comportamento di U.

Un secondo filone didattico riguarda le reazioni chimiche: guardando i profili energetici, la differenza tra energia dei reagenti e dei prodotti, corretta per il lavoro e il calore scambiati, diventa un racconto chiaro di dove “va” l’energia interna. È anche il punto di contatto con entalpia ed energie libere, strumenti quotidiani in chimica e biochimica.

Infine, nei gas reali vicini alla liquefazione o in miscele non ideali, l’energia potenziale di interazione inizia a contare molto. Non sorprende allora che la sola temperatura non basti a determinare U: occorre la descrizione completa del sistema, inclusa la sua struttura di interazione.

L’energia interna è la misura globale dell’energia “dentro” la materia, somma armonizzata di contributi cinetici e potenziali che si manifesta nei cambi di temperatura, nei lavori di compressione/espansione e nei riassetti chimici. Conoscere U e come varia significa leggere correttamente scambi di calore e lavoro, riconoscere il ruolo delle forze intermolecolari e usare con consapevolezza gli altri potenziali termodinamici (H, A, G) per scegliere la descrizione più adatta al problema concreto.