A classificação de números reais é uma parte fundamental da matemática, que envolve a categorização e organização dos diferentes tipos de números que existem. Os números reais podem ser classificados de diversas formas, como números inteiros, números racionais, números irracionais e números complexos. Essa classificação é importante para facilitar a compreensão e manipulação dos números em diversas áreas da matemática e ciências aplicadas. Neste contexto, é essencial compreender as propriedades e relações entre os diferentes tipos de números reais para resolver problemas e realizar cálculos de forma eficaz.
Guia prático para a classificação dos números reais em diferentes categorias matemáticas.
Os números reais são classificados em diferentes categorias matemáticas com base em suas propriedades e características. Neste guia prático, vamos explorar as principais categorias de números reais e como eles se encaixam dentro do conjunto dos números reais.
Para começar, os números reais podem ser divididos em duas categorias principais: os números racionais e os números irracionais. Os números racionais são aqueles que podem ser expressos como uma fração, ou seja, são números que podem ser escritos na forma $a/b$, onde $a$ e $b$ são inteiros e $b$ é diferente de zero. Por outro lado, os números irracionais são aqueles que não podem ser expressos como uma fração e têm uma expansão decimal infinita e não periódica.
Dentro da categoria dos números racionais, temos os números inteiros e os números fracionários. Os números inteiros são aqueles que não têm parte decimal, ou seja, são números sem fração. Eles incluem os números positivos, negativos e o zero. Já os números fracionários são aqueles que têm uma parte decimal, representada por uma fração. Por exemplo, 1/2, 3/4, 5/8, etc.
Por fim, os números reais também podem ser classificados como números negativos e números positivos. Os números negativos são aqueles menores que zero, enquanto os números positivos são aqueles maiores que zero. O zero é considerado um número neutro, pois não é nem positivo nem negativo.
Em resumo, os números reais podem ser classificados em diferentes categorias matemáticas, como números racionais, números irracionais, números inteiros, números fracionários, números negativos e números positivos. Compreender essas categorias e suas propriedades é essencial para estudar e trabalhar com números reais de forma eficaz.
Quem são os integrantes do grupo dos reais?
Os números reais são aqueles que podem ser representados por uma reta numérica infinita e contínua. Eles englobam os números inteiros, fracionários e decimais, além dos irracionais. Em outras palavras, todos os números que não são imaginários fazem parte do grupo dos reais.
Os integrantes do grupo dos reais são divididos em duas categorias principais: os números racionais e os números irracionais. Os números racionais são aqueles que podem ser expressos como uma fração, ou seja, podem ser representados por um quociente de dois inteiros. Por exemplo, 1/2, 3/4, -5/7 são todos números racionais.
Por outro lado, os números irracionais são aqueles que não podem ser expressos como uma fração. Eles têm uma representação decimal infinita e não periódica, como é o caso de √2, π e e. Esses números são infinitos e não podem ser escritos de forma exata, sendo representados por uma sequência não repetitiva de algarismos.
Portanto, os integrantes do grupo dos reais são todos os números que podem ser representados em uma reta numérica, incluindo os números racionais e irracionais. Eles formam um conjunto completo e abrangente de números que utilizamos em diversas situações do nosso dia a dia.
Listando os 5 conjuntos que você precisa conhecer agora mesmo!
Na classificação de números reais, é essencial conhecer os cinco conjuntos principais que são fundamentais para diversos cálculos e análises matemáticas. Estes conjuntos são: os números naturais, os números inteiros, os números racionais, os números irracionais e os números reais.
Os números naturais são os números positivos utilizados para contar objetos e são representados por N={0, 1, 2, 3, …}. Já os números inteiros incluem os números positivos, negativos e o zero, representados por Z={… -3, -2, -1, 0, 1, 2, 3, …}.
Os números racionais são aqueles que podem ser expressos como uma fração, representados por Q. Eles incluem todos os inteiros e frações. Por outro lado, os números irracionais são números que não podem ser expressos como frações e têm uma representação decimal infinita e não periódica.
Por fim, os números reais englobam todos os números racionais e irracionais, formando a reta numérica completa. Eles são representados por R e são essenciais para resolver equações e realizar operações matemáticas complexas.
A compreensão desses cinco conjuntos é fundamental para qualquer estudante ou profissional que trabalha com matemática. Portanto, é importante familiarizar-se com cada um deles e entender suas propriedades e aplicações em diversas situações do dia a dia.
Quais são os números que não pertencem ao conjunto dos números reais?
Os números que não pertencem ao conjunto dos números reais são os números complexos. Os números complexos são representados na forma a + bi, onde “a” e “b” são números reais e “i” é a unidade imaginária, que é a raiz quadrada de -1.
Os números reais, por sua vez, incluem todos os números racionais e irracionais. Os números racionais são aqueles que podem ser expressos como uma fração, enquanto os números irracionais são aqueles que não podem ser expressos como uma fração simples e têm uma expansão decimal infinita e não periódica.
Portanto, os números complexos, que incluem a parte real e a parte imaginária, não pertencem ao conjunto dos números reais. Eles são uma extensão dos números reais e são essenciais em muitos campos da matemática e da física.
Classificação de números reais
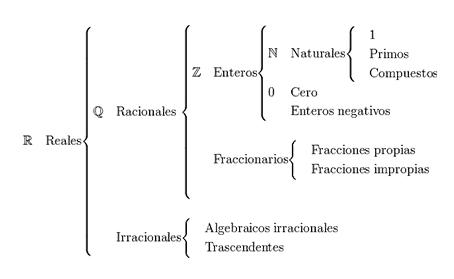
A principal classificação dos números reais é dividida em números naturais, números inteiros, números racionais e números irracionais. Os números reais são representados com a letra R.
Há muitas maneiras pelas quais diferentes números reais podem ser construídos ou descritos, variando de formas mais simples a mais complexas, dependendo do trabalho matemático que você deseja executar.
Como os números reais são classificados?
Números naturais
Estes são os números usados para contar, como “existem quatro flores no copo”.
Algumas definições começam com números naturais em 0, enquanto outras definições começam em 1. Números naturais são aqueles usados para contar: 1,2,3,4,5,6,7,8,9,10 … etc; Eles são usados como números ordinais ou cardinais.
Números naturais são as bases com as quais muitos outros conjuntos de números podem ser construídos por extensão: números inteiros, números racionais, números reais e números complexos, entre outros.
Essas cadeias de extensão compõem os números naturais identificados canonicamente nos outros sistemas numéricos.
As propriedades dos números naturais, como divisibilidade e distribuição de números primários, são estudadas na teoria dos números.
Problemas relacionados à contagem e ordenação, como enumerações e partições, são estudados na combinatória.
Em linguagem comum, como nas escolas primárias, os números naturais podem ser chamados de números contáveis para excluir números inteiros negativos e zero.
Eles têm várias propriedades, tais como: adição, multiplicação, subtração, divisão, etc.
Números inteiros
Inteiros são aqueles números que podem ser escritos sem um componente fracionário. Por exemplo: 21, 4, 0, -76, etc. Por outro lado, números como 8,58 ou √2 não são números inteiros.
Você pode dizer que os números inteiros são os números completos, juntamente com os negativos dos números naturais. Eles são usados para expressar dinheiro devido, profundidades em relação ao nível do mar ou temperatura abaixo de zero, para citar alguns usos.
Um conjunto de números inteiros consiste em zero (0), números naturais positivos (1,2,3 …) e números negativos (-1, -2, -3 …). Geralmente, isso é chamado com um ZZ ou com um Z (Z) em negrito.
Z é um subconjunto do grupo de números racionais Q, que por sua vez forma o grupo de números reais R. Como os números naturais, Z é um grupo contábil infinito.
Os números inteiros formam o menor grupo e o menor conjunto de números naturais. Na teoria dos números algébricos, os números inteiros às vezes são chamados números inteiros irracionais para distingui-los dos números inteiros algébricos.
Números racionais
Um número racional é qualquer número que pode ser expresso como o componente ou fração de dois números inteiros p / q, um numerador p e um denominador q. Como q pode ser igual a 1, cada número inteiro é um número racional.
O conjunto de números racionais, geralmente chamado de “os racionais”, é indicado com um Q.
A expansão decimal de um número racional sempre termina após um número finito de dígitos ou quando você começa a repetir a mesma sequência finita de dígitos repetidamente.
Além disso, qualquer decimal ou terminal repetido representa um número racional. Essas instruções são verdadeiras não apenas para a base 10, mas também para qualquer outra base inteira.
Um número real que não é racional é chamado irracional. Os números irracionais incluem √2, a e π, por exemplo. Como todo o conjunto de números racionáveis é contável e que o grupo de números reais não é contável, pode-se dizer que quase todos os números reais são irracionais.
Os números racionais podem ser formalmente definidos como classes de equivalência de pares inteiros (p, q), de modo que q ≠ 0 ou a razão equivalente definida por (p1, q1) (p2, q2) somente se p1, q2 = p2q1.
Números racionais, juntamente com adição e multiplicação, formam campos que compõem números inteiros e são contidos por qualquer ramificação que contenha números inteiros.
Números irracionais
Números irracionais são todos números reais que não são racionais; Números irracionais não podem ser expressos como frações. Números racionais são números compostos de frações de números inteiros.
Como resultado do teste de Cantor, que afirma que todos os números reais são não numeráveis e que os racionais são numeráveis, pode-se concluir que quase todos os números reais são irracionais.
Quando o raio do comprimento de dois segmentos de linha é um número irracional, pode-se dizer que esses segmentos de linha são incomensuráveis; significando que não há um comprimento suficiente para que cada um deles possa ser “medido” com um determinado número inteiro múltiplo.
Entre os números irracionais estão o raio π de uma circunferência circular em relação ao seu diâmetro, o número de Euler (e), o número dourado (φ) e a raiz quadrada de dois; ainda mais, todas as raízes quadradas dos números naturais são irracionais. A única exceção a essa regra são os quadrados perfeitos.
Pode-se observar que, quando números irracionais são expressos posicionalmente em um sistema numeral (como, por exemplo, em números decimais), eles não terminam ou são repetidos.
Isso significa que eles não contêm uma sequência de dígitos, a repetição pela qual uma linha de representação é feita.
Por exemplo: a representação decimal do número π começa com 3,14159265358979, mas não há um número finito de dígitos que possam representar com precisão π, nem que possam ser repetidos.
A prova de que a expansão decimal de um número racional deve terminar ou ser repetida é diferente da prova de que uma extensão decimal deve ser um número racional; Embora básicos e um pouco longos, esses testes exigem algum trabalho.
Normalmente, os matemáticos geralmente não adotam a noção de “finalização ou repetição” para definir o conceito de um número racional.
Os números irracionais também podem ser tratados por frações não contínuas.
Referências
- Classificação de números reais. Recuperado de chilimath.com.
- Número natural Recuperado de wikipedia.org.
- Classificação dos números. Recuperado de ditutor.com.
- Recuperado de wikipedia.org.
- Número irracional Recuperado de wikipedia.org.