Frações e decimais: diferenças, semelhanças e usos práticos

Início » Ciência » Matemática » Frações e decimais: diferenças, semelhanças e usos práticos

Se você já pesou 1/2 kg de café ou calculou o troco de R$ 5,00 para uma compra de R$ 2,80, já usou frações e números decimais sem nem perceber. Essas duas linguagens numéricas descrevem a mesma ideia de quantidade, mas com formas de escrita e regras próprias, e convivem desde a sala de aula até a vida cotidiana.

Ao longo deste guia completo, vamos ligar os pontos entre história, definições, conversões e operações, do jeitinho que aparece no ensino fundamental e no médio no Brasil. Você verá onde frações e decimais se encontram, onde diferem, e como aplicar cada uma com segurança: ler e escrever decimais, somar e subtrair com vírgula alinhada, multiplicar e dividir por potências de 10, comparar valores e até resolver problemas práticos — incluindo porcentagens e situações de prova.

O que são frações e decimais

Uma fração é um número racional escrito na forma a/b, em que a é o numerador e b (≠ 0) é o denominador. Ela expressa quantas partes (numerador) tomamos de um todo dividido em partes iguais (denominador).

Já o número decimal apresenta parte inteira e parte decimal separadas por vírgula (no padrão brasileiro). Você pode enxergar o decimal como uma “tradução” de frações cujo denominador é potência de 10 — por exemplo, 127/100 = 1,27 e 8/10 = 0,8.

Tipos de frações

Fração própria: numerador menor que denominador (por exemplo, 3/4). Representa menos que uma unidade inteira.

Fração imprópria: numerador maior que denominador (por exemplo, 7/3). Representa mais que um inteiro.

Fração mista: combinação de parte inteira com uma fração própria (por exemplo, 2 1/5). Ela é outra forma de escrever uma fração imprópria, como 11/5 no exemplo.

Frações equivalentes: têm o mesmo valor, embora escritas de forma diferente, caso numerador e denominador sejam multiplicados ou divididos pelo mesmo número (por exemplo, 2/4 = 1/2; 15/10 = 3/2). Reduzir uma fração é encontrar sua forma irredutível.

Fração irredutível: quando não há divisor comum (além de 1) para numerador e denominador, ou seja, não dá para simplificar mais (por exemplo, 3/5).

Decimais e a ideia de potência de 10

Frações decimais são aquelas cujo denominador é 10, 100, 1000 etc. Todo decimal finito corresponde a uma fração decimal (0,5 = 5/10; 2,41 = 241/100; 7,345 = 7345/1000) e vice-versa (130/100 = 1,30; 5/1000 = 0,005).

Um pouco de história: do Egito a Stevin e Napier

O uso de frações nasceu da necessidade de medir. Os egípcios priorizavam frações unitárias, do tipo 1/n (como 1/2, 1/3, 1/4), e combinavam frações unitárias para formar outras (por exemplo, 5/6 = 1/2 + 1/3).

Os babilônios trabalharam com base 60, muito por ser um número “rico” em divisores. Já os romanos usavam divisões frequentes em 12 partes, explorando um denominador também bem divisível.

No século XVI, consolidou-se a notação moderna de frações e, em 1585, Simon Stevin propôs um modo de calcular apenas com inteiros, indicando a posição decimal. Em 1617, John Napier difundiu o uso de ponto ou vírgula separando parte inteira e decimal, padrão que encurtou contas e ganhou fôlego com o sistema métrico decimal. Por muito tempo, decimais foram famosos nos cálculos astronômicos pela precisão que proporcionavam.

Leitura e escrita de números decimais

Para ler um decimal, identifique a vírgula que separa parte inteira (PI) e parte decimal (PD). A posição dos dígitos depois da vírgula define se são décimos, centésimos, milésimos e assim por diante.

• 0,6: “seis décimos”. Aqui não há parte inteira.
• 0,37: “trinta e sete centésimos”.
• 0,189: “cento e oitenta e nove milésimos”.
• 3,7: “três inteiros e sete décimos”.
• 13,45: “treze inteiros e quarenta e cinco centésimos”.
• 130,824: “cento e trinta inteiros e oitocentos e vinte e quatro milésimos”.

Você também pode anexar zeros à direita da parte decimal sem alterar o valor (0,5 = 0,50 = 0,500). Isso é útil para alinhar casas decimais em operações, leitura e comparação.

Multiplicar por 10, 100, 1000 desloca a vírgula para a direita em 1, 2, 3 casas, respectivamente: 7,4 × 10 = 74; 7,4 × 100 = 740; 7,4 × 1000 = 7400. É um atalho prático em contas do dia a dia.

Dividir por 10, 100, 1000 desloca a vírgula para a esquerda na mesma quantidade de casas: 247,5 ÷ 10 = 24,75; ÷ 100 = 2,475; ÷ 1000 = 0,2475. Observe como o número “encolhe” a cada divisão por 10.

Transformações entre frações e decimais

Para passar de fração decimal (denominador 10, 100, 1000…) para decimal, basta “posicionar” a vírgula de acordo com os zeros do denominador: 130/100 = 1,30; 987/1000 = 0,987; 5/1000 = 0,005. Na prática, é a divisão do numerador pelo denominador.

Do contrário, para converter decimal em fração decimal, escreva como numerador o número sem a vírgula e, como denominador, 1 seguido de tantos zeros quantas forem as casas decimais: 0,5 = 5/10; 0,05 = 5/100; 2,41 = 241/100; 7,345 = 7345/1000. Simplifique quando possível para obter a forma irredutível.

É comum precisar igualar o número de casas decimais “colando zeros” à direita (como 1,7 e 1,700). Isso não muda o valor e facilita comparações e somas/subtrações.

Operações com números decimais

Adição e subtração

Regra de ouro: alinhe as vírgulas e garanta o mesmo número de casas decimais, adicionando zeros se necessário. Depois some ou subtraia coluna por coluna, como com inteiros.

Exemplo de soma: 2,4 + 1,713 → escreva 2,400 + 1,713 = 4,113. O alinhamento preserva décimos, centésimos e milésimos em suas colunas.

Exemplo de subtração: 2,4 − 1,713 → 2,400 − 1,713 = 0,687. A vírgula do resultado cai exatamente na coluna das vírgulas alinhadas.

Multiplicação

Você pode transformar os fatores em frações decimais e multiplicar numeradores e denominadores (2,25 × 3,5 = 225/100 × 35/10 = 7875/1000 = 7,875). É a leitura “fracionária” do produto.

Outra forma é multiplicar como inteiros e, no final, contar as casas decimais totais dos fatores para posicionar a vírgula no produto: em 2,25 (duas casas) × 3,5 (uma casa), o resultado tem três casas → 7,875. Esse método costuma ser o mais rápido no papel.

Divisão

Quando há vírgula no divisor, “corte” a vírgula multiplicando dividendo e divisor pela mesma potência de 10 até o divisor virar inteiro. Isso não altera o quociente. Exemplo: 3,6 ÷ 0,4 → (36 ÷ 4) = 9.

Se o dividendo for decimal e o divisor inteiro, você também pode “limpar” a vírgula multiplicando ambos por 10, 100 etc. Exemplo: 0,35 ÷ 7 → (35 ÷ 700) = 0,05. Note como duas casas no dividendo pedem multiplicar por 100.

Dividindo um número por outro maior: 35 ÷ 700. É útil pensar em 3500 ÷ 700 e ajustar a vírgula no quociente (dois zeros “emprestados” pedem duas casas decimais). Assim, 35/700 = 0,05.

Divisão típica que não dá inteiro: 10 ÷ 16. Transforme 10 em 100 (colocando 0 no quociente após a vírgula), faça 100 ÷ 16 = 6 (resto 4); traga um zero → 40 ÷ 16 = 2 (resto 8); traga outro zero → 80 ÷ 16 = 5 (resto 0). Logo, 10 ÷ 16 = 0,625, um decimal exato.

Operações com frações

Soma e subtração com mesmo denominador

Repita o denominador e opere apenas os numeradores (como 3/10 + 7/10 = 10/10 = 1). O denominador comum é a base do “estoque” de partes.

Soma e subtração com denominadores diferentes

Encontre um denominador comum (de preferência o MMC) e reescreva as frações equivalentes. Exemplo genérico: a/b e c/d → (ad)/(bd) e (cb)/(bd). Depois some ou subtraia os novos numeradores.

Multiplicação e divisão

Na multiplicação, numerador com numerador e denominador com denominador: 2/3 × 5/4 = 10/12 = 5/6. Simplificar antes de multiplicar costuma reduzir contas.

Na divisão, mantém a primeira fração e multiplica pelo inverso da segunda: (3/5) ÷ (2/7) = (3/5) × (7/2) = 21/10 = 2,1. Lembre do “vira o de trás e multiplica” para fixar a ideia.

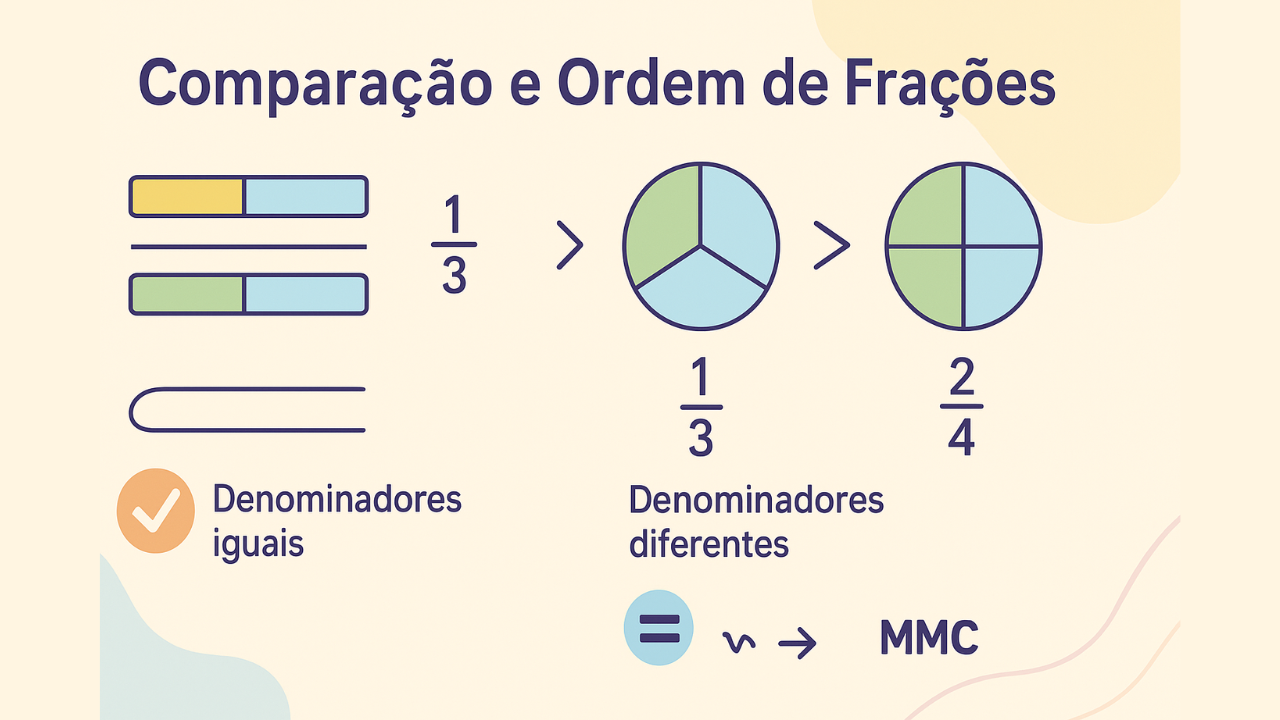
Comparação de números decimais

Se as partes inteiras são diferentes, vence quem tem a parte inteira maior: 4,1 > 2,76 e 3,7 < 5,4. Nesse caso, nem precisa olhar a parte decimal.

Se as partes inteiras são iguais, iguale o número de casas decimais adicionando zeros e compare a parte decimal como se fosse inteiro: 12,4 e 12,31 → 12,40 e 12,31, logo 12,4 > 12,31. Outro exemplo: 8,032 e 8,47 → 8,032 e 8,470, portanto 8,032 < 8,47.

Comparação de frações

Com denominadores iguais, compare apenas numeradores: quem tem numerador maior representa mais partes do mesmo todo. Assim, 4/9 > 2/9 e 15/22 > 7/22.

Com denominadores diferentes, reduza ao mesmo denominador (ou use a “regra prática” do produto cruzado): compare a×d e c×b em a/b e c/d. Quem tiver o maior produto cruzado é a maior fração.

Porcentagens, proporções e aplicações

Porcentagem significa “por cento”, isto é, uma fração com denominador 100. Escrevemos 30% como 30/100, o que ajuda a converter para decimal (0,30) e resolver problemas.

• Se 30% da turma são meninas, isso equivale a 30/100 do total. Em uma turma de 100, seriam 30 meninas.
• 40% de R$ 300,00: resolvemos 40/100 = X/300 → 100X = 12.000 → X = 120. Portanto, 40% de 300 é 120.
• Li 45% de um livro de 200 páginas: 45/100 = X/200 → 100X = 9000 → X = 90 lidas; faltam 200 − 90 = 110 páginas. Transformar em proporção deixa o raciocínio transparente.

Exemplos práticos do dia a dia

No mercado: 1/2 kg de café a R$ 2,80 e pagamento com R$ 5,00. O troco é 5,00 − 2,80 = 2,20. Nesse exemplo, usamos fração (1/2 kg), decimais em reais e subtração com vírgula alinhada.

Doação de terra: 35 medidas para 700 pessoas, cada medida com 24.200 m². Primeiro, 35/700 = 0,05 (como vimos acima). Então, cada pessoa recebe 0,05 × 24.200 = 1.210 m². Total conferindo: 1.210 × 700 = 847.000 m², que é 35 × 24.200.

Trabalhando com potências de 10 para simplificar contas: multiplicar 24,2 por 100 rende 2420 (vírgula anda 2 casas). O mesmo raciocínio vale para dividir e reajustar a posição da vírgula.

Quando o número do divisor tem vírgula (por exemplo, 0,4), “limpe” multiplicando ambos por 10 até obter um divisor inteiro (3,6 ÷ 0,4 → 36 ÷ 4 = 9). Esse truque torna a divisão muito mais direta.

Conjuntos numéricos e o lugar de frações e decimais

Os números se organizam em conjuntos: naturais (0, 1, 2, …), inteiros (…, −2, −1, 0, 1, …), racionais (frações e decimais finitos ou periódicos) e reais (incluindo irracionais como √2). Frações estão no conjunto dos racionais, e todo decimal exato pode ser escrito como fração decimal (veja a localização de números inteiros e decimais).

Na prática escolar, focamos nas propriedades que garantem as operações: associativas, comutativas (exceto na divisão), distributiva, existência de elementos neutros e inversos (quando definidos). Esse arcabouço explica por que as transformações entre frações e decimais funcionam tão bem.

Frações e decimais no ENEM e em provas

Questões de provas costumam testar intuições equivocadas. Pegue este caso: “Para números decimais positivos, I) o produto de dois números é sempre maior que cada fator; II) a soma de dois números é sempre maior que cada parcela; III) a divisão entre dois números nunca dá natural”. A alternativa correta é apenas a II.

Por quê? Porque 0,5 × 0,5 = 0,25 (produto menor que os fatores, logo I é falsa) e 0,6 ÷ 0,3 = 2 (um natural, então III é falsa). Já em somas, realmente cada parcela “aumenta” a outra, garantindo que o total supere cada uma separadamente.

Treinar conversões rápidas (0,375 ↔ 375/1000 ↔ 3/8), alinhar vírgulas em adições/subtrações e dominar o “corte de vírgula” na divisão costumam render pontos fáceis e evitar erros bobos.

Ao comparar frações em prova, lembre da estratégia do produto cruzado quando os denominadores diferem; ao comparar decimais, iguale casas. São rotas seguras para decidir maior, menor ou igual sem se perder.

Embora pareçam dois “mundos”, frações e decimais descrevem o mesmo universo de quantidades racionais. A escolha da forma depende do contexto: em dinheiro e medidas métricas, decimais são práticos; em razões exatas, receitas matemáticas e demonstrações, frações são mais transparentes.

Dominar a leitura (décimos, centésimos, milésimos), os atalhos com potências de 10, o alinhamento da vírgula e as equivalências entre representações faz com que você transite com naturalidade entre os dois formatos e resolva desde compras simples até exercícios mais longos de divisão, como 10 ÷ 16 = 0,625.

Ao ligar história (Egito, Babilônia, Roma) e notação moderna (Stevin e Napier), entendemos por que hoje é tão fácil trocar 127/100 por 1,27 com uma vírgula, fazendo contas ágeis sem perder a precisão. O que muda é apenas a “roupa” do número; o valor continua sendo o mesmo.