As aplicações da parábola na vida cotidiana são múltiplas. Desde o uso de antenas de satélite e radiotelescópios para concentrar sinais até o uso de faróis de carros ao enviar feixes de luz paralelos.
Uma parábola, em termos simples, pode ser definida como uma curva na qual os pontos são equidistantes de um ponto fixo e uma linha reta. O ponto fixo é chamado de foco e a linha é conhecida como orientação.
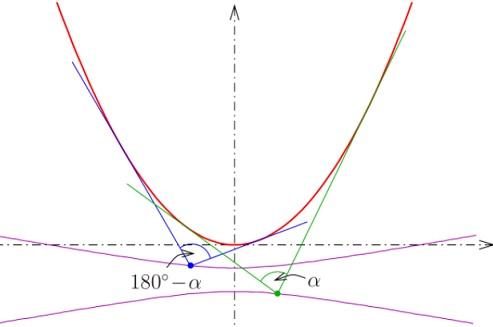
A parábola é uma cônica traçada em diferentes fenômenos, como o movimento de uma bola dirigida por um jogador de basquete ou a queda de água de uma fonte.
A parábola tem importância especial em várias áreas da física , resistência de materiais ou mecânica. Na base da mecânica e da física, são usadas as propriedades da parábola.
Às vezes, muitas pessoas dizem que estudos e trabalhos matemáticos são desnecessários na vida cotidiana porque não são aplicáveis a olho nu. Mas a verdade é que existem muitas ocasiões em que esses estudos são aplicados.
Aplicações da parábola na vida cotidiana
antenas parabólicas
A parábola pode ser definida como uma curva que surge ao fazer um corte em um cone. Se essa definição fosse aplicada a um objeto tridimensional, obteríamos uma superfície chamada parabolóide.
Esta figura é muito útil por causa de uma propriedade que as parábolas possuem, onde um ponto dentro dela está se movendo em uma linha paralela ao eixo, ele “salta” na parábola e é enviado ao foco.
Um parabolóide com um receptor de sinal no foco pode obter todos os sinais que saltam no parabolóide para serem enviados ao receptor, sem apontar diretamente para ele. Uma grande recepção de sinal é obtida usando todo o parabolóide.
Esses tipos de antenas são caracterizados por terem um refletor parabólico. Sua superfície é um parabolóide de revolução.
Sua forma é devida a uma propriedade de parábolas matemáticas. Eles podem ser transmissores, receptores ou full duplex. Eles são chamados assim quando são capazes de transmitir e receber ao mesmo tempo. Eles são geralmente usados em altas frequências.
Satélites
Um satélite envia informações para a Terra. Esses raios são perpendiculares à diretriz devido à distância que está no satélite.
Quando refletidos na placa da antena, que geralmente é branca, os raios convergem no foco em que um receptor decodifica a informação.
Jatos de água
Os jatos de água que saem de um bico têm uma forma parabólica.
Quando inúmeros jatos saem de um ponto com velocidade igual, mas com inclinação diferente, outra parábola chamada “parábola de segurança” está acima dos outros e não é possível passar por nenhuma outra parábola restante acima dele.
Fogões solares
A propriedade que caracteriza as parábolas permite que elas sejam usadas para criar dispositivos como fogões solares.
Com um parabolóide que reflete os raios do sol, o que será cozido será facilmente colocado em seu foco, fazendo com que ele aqueça rapidamente.
Outros usos são o acúmulo de energia solar usando um acumulador no centro das atenções.
Faróis de veículos e microfones parabólicos
A propriedade das parábolas explicada anteriormente pode ser usada ao contrário. Quando um emissor de sinal localizado em direção à sua superfície é colocado no foco de um parabolóide, todos os sinais refletem sobre ele.
Dessa maneira, seu eixo será refletido paralelamente para fora, obtendo um nível mais alto de emissão de sinal.
Nos faróis dos veículos, isso ocorre quando uma lâmpada é colocada no foco para emitir mais luz.
Nos microfones parabólicos, ocorre quando um microfone é colocado no foco de um parabolóide para emitir uma quantidade maior de som.
Pontes suspensas
Os cabos suspensos assumem a forma parabólica. Estes formam o envelope de uma parábola.
Na análise da curva de equilíbrio dos cabos, admite-se que são numerosos suportes e a carga pode ser considerada distribuída uniformemente na horizontal.
Com esta descrição, é mostrado que a curva de equilíbrio de cada cabo é uma simples parábola de equação e seu uso é frequente na técnica.
Exemplos da vida real são a ponte de São Francisco (Estados Unidos) ou a ponte Barqueta (Sevilha), que usa estruturas parabólicas para dar maior estabilidade à ponte.
Caminho do objeto celeste
Existem pipas periódicas que possuem trajetórias alongadas elípticas.
Quando os cometas ao redor do sistema solar não são demonstrados, eles parecem descrever uma parábola.
Esportes
Em todo esporte em que um arremesso é feito, encontramos parábolas. Estes podem ser descritos por bolas ou artefatos lançados como no futebol, basquete ou lançamento de dardo.
Esse lançamento é conhecido como “lançamento parabólico” e consiste em puxar (não verticalmente) algum objeto.
O caminho que o objeto faz ao subir (com a força aplicada a ele) e descer (por gravidade) forma uma parábola.
Um exemplo mais concreto são os movimentos feitos por Michael Jordan, jogador de basquete da NBA.
Este jogador tornou-se famoso, entre outras coisas, por seus “vôos” para a cesta onde, à primeira vista, ele parecia estar suspenso no ar por muito mais tempo do que outros jogadores.
O segredo de Michael era que ele sabia usar movimentos corporais adequados e uma grande velocidade inicial que lhe permitia formar uma parábola alongada, tornando sua trajetória próxima à altura do vértice.
Iluminação
Quando um feixe de luz cônico é projetado na parede, são obtidas formas parabólicas, desde que a parede seja paralela à geratriz do cone.
Referências
- Arnheim, C. (2015). Superfícies Matemáticas. Alemanha: BoD
- Boyer, C. (2012). História da Geometria Analítica . EUA: Courier Corporation.
- Frante, Ronald L. Uma antena parabólica com lóbulos laterais muito baixos. Transações IEEE em Antenas e Propagação. Vol. 28, N0. 1. Jan 1980. Pp 53-59.
- Kletenik, D. (2002). Problemas em geometria analítica. Havaí: O Grupo Minerva.
- Kraus, JD (1988). Antenas , 2ª Ed. EUA: McGraw-Hill.
- Lehmann, C. (1984). Geometria analítica. México: Limusa.