O plano cartesiano é uma ferramenta matemática fundamental que permite a representação de pontos em um espaço bidimensional por meio de coordenadas. Desenvolvido pelo filósofo e matemático francês René Descartes, o plano cartesiano possui cinco características principais que o tornam uma ferramenta indispensável para a geometria analítica e a resolução de problemas matemáticos. Essas características incluem a divisão do plano em quatro quadrantes, a representação de pontos por pares ordenados, a definição de eixos coordenados, a distância entre pontos e a interpretação de relações matemáticas por meio de equações e gráficos.
Descubra as principais características do plano cartesiano em apenas algumas palavras.
Descubra as principais características do plano cartesiano em apenas algumas palavras.
1. Eixos coordenados: O plano cartesiano possui dois eixos perpendiculares, o eixo horizontal chamado de eixo das abscissas e o eixo vertical chamado de eixo das ordenadas.
2. Origem: O ponto de interseção dos eixos é chamado de origem, representado pelo par ordenado (0,0).
3. Coordenadas: Cada ponto no plano cartesiano é representado por um par ordenado de números, onde o primeiro número representa a coordenada no eixo das abscissas e o segundo número representa a coordenada no eixo das ordenadas.
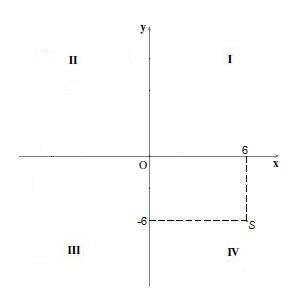
4. Quadrantes: O plano cartesiano é dividido em quatro quadrantes, numerados de I a IV, a partir do sentido anti-horário a partir do primeiro quadrante no sentido positivo dos eixos.
5. Distância entre pontos: A distância entre dois pontos no plano cartesiano pode ser calculada utilizando a distância euclidiana, que é a raiz quadrada da soma dos quadrados das diferenças das coordenadas.
Elementos que compõem o plano cartesiano: coordenadas, eixos, quadrantes e ponto de origem.
O plano cartesiano é uma ferramenta fundamental da matemática que nos permite representar graficamente pontos e funções matemáticas. É composto por quatro elementos principais: coordenadas, eixos, quadrantes e ponto de origem. Neste artigo, vamos discutir as 5 características mais importantes do plano cartesiano.
1. Coordenadas: As coordenadas são pares de números que indicam a localização de um ponto no plano cartesiano. Elas são representadas por (x, y), onde x representa a posição do ponto no eixo horizontal (eixo x) e y representa a posição do ponto no eixo vertical (eixo y).
2. Eixos: Os eixos do plano cartesiano são duas linhas perpendiculares que se cruzam no ponto de origem. O eixo horizontal é chamado de eixo x e o eixo vertical é chamado de eixo y. Eles são usados para determinar a posição dos pontos no plano.
3. Quadrantes: O plano cartesiano é dividido em quatro quadrantes, numerados de I a IV, no sentido anti-horário a partir do quadrante superior direito. Cada quadrante possui características específicas que nos ajudam a localizar pontos no plano.
4. Ponto de origem: O ponto de origem é o ponto onde os eixos x e y se cruzam. Ele possui coordenadas (0, 0) e é considerado o ponto de referência para todos os outros pontos no plano cartesiano.
5. Simetria: Uma das principais características do plano cartesiano é a sua simetria em relação ao ponto de origem. Isso significa que pontos simétricos em relação aos eixos possuem coordenadas opostas, o que facilita o estudo de simetrias e transformações geométricas.
Em resumo, o plano cartesiano é uma ferramenta poderosa que nos permite visualizar e trabalhar com conceitos matemáticos de forma mais clara e precisa. Compreender os elementos e características do plano cartesiano é essencial para o estudo da geometria e da álgebra.
O significado do plano cartesiano e exemplos práticos para sua compreensão.
O plano cartesiano é um sistema de coordenadas criado pelo matemático francês René Descartes no século XVII. Ele é composto por dois eixos perpendiculares, o eixo horizontal chamado de eixo x e o eixo vertical chamado de eixo y. Esses eixos se cruzam em um ponto chamado de origem, que possui as coordenadas (0,0).
Existem 5 características principais do plano cartesiano que ajudam a compreender melhor a sua estrutura e funcionamento:
1. Eixos perpendiculares: Os eixos x e y são perpendiculares entre si, formando quatro quadrantes no plano cartesiano.
2. Origem: O ponto de interseção dos eixos x e y é chamado de origem, representado pelas coordenadas (0,0).
3. Coordenadas: Qualquer ponto no plano cartesiano pode ser representado por um par de coordenadas (x,y), onde x é a distância do ponto até o eixo y e y é a distância do ponto até o eixo x.
4. Quadrantes: O plano cartesiano é dividido em quatro quadrantes, numerados de I a IV no sentido anti-horário a partir do primeiro quadrante, que fica no lado superior direito do plano.
5. Distância entre pontos: A distância entre dois pontos no plano cartesiano pode ser calculada utilizando o teorema de Pitágoras, considerando as diferenças entre as coordenadas x e y dos pontos.
Um exemplo prático do uso do plano cartesiano é a representação de gráficos de funções matemáticas. Por exemplo, a função f(x) = x² pode ser representada no plano cartesiano plotando os pontos cujas coordenadas são (x, f(x)). Isso permite visualizar a forma da curva da função e analisar seu comportamento em diferentes intervalos.
Entendendo o plano cartesiano: passo a passo para compreender sua representação gráfica.
O plano cartesiano é uma ferramenta matemática fundamental que permite representar geometricamente pontos, retas e figuras. Composto por dois eixos perpendiculares, o plano cartesiano foi criado pelo matemático francês René Descartes no século XVII. Para compreender sua representação gráfica, é importante estar ciente de suas principais características.
5 Características do plano cartesiano:
1. Eixos coordenados: O plano cartesiano é formado por dois eixos perpendiculares, o eixo horizontal (eixo das abscissas) e o eixo vertical (eixo das ordenadas). Eles se encontram no ponto chamado de origem.
2. Coordenadas: Cada ponto no plano cartesiano é representado por um par de números ordenados, que correspondem à sua posição nos eixos. O primeiro número indica a posição ao longo do eixo horizontal, e o segundo número indica a posição ao longo do eixo vertical.
3. Quadrantes: O plano cartesiano é dividido em quatro quadrantes, numerados de I a IV. Cada quadrante possui características específicas em relação aos sinais das coordenadas dos pontos que o compõem.
4. Distância: A distância entre dois pontos no plano cartesiano pode ser calculada utilizando a fórmula da distância entre dois pontos no espaço euclidiano.
5. Representação gráfica: A representação gráfica de funções no plano cartesiano permite visualizar de forma clara e objetiva o comportamento de variáveis em um sistema de coordenadas.
Compreender as características do plano cartesiano é essencial para a resolução de problemas matemáticos e a interpretação de resultados. Dominar essa ferramenta possibilita uma melhor compreensão da geometria analítica e da matemática em geral.
5 Características do plano cartesiano
O plano cartesiano, ou sistema de coordenadas cartesianas , é uma área bidimensional (perfeitamente plana) que contém um sistema no qual os pontos podem ser identificados por sua posição usando um par ordenado de números.
Este par de números representa a distância dos pontos a um par de eixos perpendiculares. Os eixos são chamados de eixo x ( eixo horizontal ou abscissa) e eixo y ( eixo vertical ou ordenado).
Dessa maneira, a posição de qualquer ponto é definida com um par de números no formato (x, y). Portanto, x é a distância do ponto ao eixo x, enquanto y é a distância do ponto ao eixo y.
Esses planos são chamados cartesianos, derivado de Cartesius, o nome latino do filósofo francês René Descartes (que viveu entre o final do século XVI e a primeira metade do século XVII). Foi esse filósofo que desenvolveu o avião pela primeira vez.
Breve explicação das características do plano cartesiano
O plano cartesiano possui extensão e ortogonalidade infinitas nos eixos
Tanto o eixo X como o eixo e prolongar infinitamente em ambas as extremidades, e perpendicularmente se cruzam uns aos outros (com um ângulo de 90 graus). Esse recurso é chamado de ortogonalidade.
O ponto em que os dois eixos se cruzam é conhecido como origem ou ponto zero. No eixo x , a seção à direita da origem é positiva e à esquerda negativa. No eixo y , a seção acima da origem é positiva e abaixo, negativa.
O plano cartesiano divide a área bidimensional em quatro quadrantes
O sistema de coordenadas divide o plano em quatro regiões chamadas quadrantes . O primeiro quadrante tem a parte positiva do eixo x e do eixo y .
Por seu lado, o segundo quadrante tem a parte negativa do eixo xe a parte positiva do eixo y . O terceiro quadrante possui a parte negativa do eixo xe a parte negativa do eixo y . Finalmente, o quarto quadrante possui a parte positiva do eixo xe a parte negativa do eixo y .
Os locais no plano de coordenadas são descritos como pares ordenados
Um par ordenado informa a localização de um ponto, relacionando a localização do ponto ao longo do eixo x (o primeiro valor do par ordenado) e ao longo do eixo y (o segundo valor do par ordenado).
Em um par ordenado, como (x, y), o primeiro valor é chamado de coordenada x e o segundo valor é a coordenada y . A coordenada x é listada antes da coordenada y .
Como a origem tem uma coordenada x de 0 e uma coordenada y de 0, seu par ordenado é gravado (0,0).
Os pares ordenados de um plano cartesiano são únicos
Cada ponto no plano cartesiano está associado a uma coordenada x única e a uma coordenada única. A localização deste ponto no plano cartesiano é final.
Depois que as coordenadas (x, y) tiverem sido definidas para o ponto, não haverá outra com as mesmas coordenadas.
O sistema de coordenadas cartesianas representa graficamente as relações matemáticas
O plano de coordenadas pode ser usado para desenhar pontos e linhas de gráficos.Este sistema permite descrever as relações algébricas em sentido visual.
Também ajuda a criar e interpretar conceitos algébricos. Como aplicação prática da vida cotidiana, é possível mencionar o posicionamento em mapas e planos cartográficos.
Referências
- Hatch, SA e Hatch, L. (2006). GMAT para manequins. Indianapolis: John Wiley & Sons.
- Importância (s / f). Importância do plano cartesiano. Retirado em 10 de janeiro de 2018, de important.org.
- Pérez Porto, J. e Merino, M. (2012). Definição de plano cartesiano. Recuperado em 10 de janeiro de 2018, de definicion.de.
- Ibañez Carrasco, P. e García Torres, G. (2010). Matemática III. Cidade do México: Cengage Learning Editors.
- Instituto Monterey (s / f). O plano de coordenadas. Recuperado em 10 de janeiro de 2018, de montereyinstitute.org.