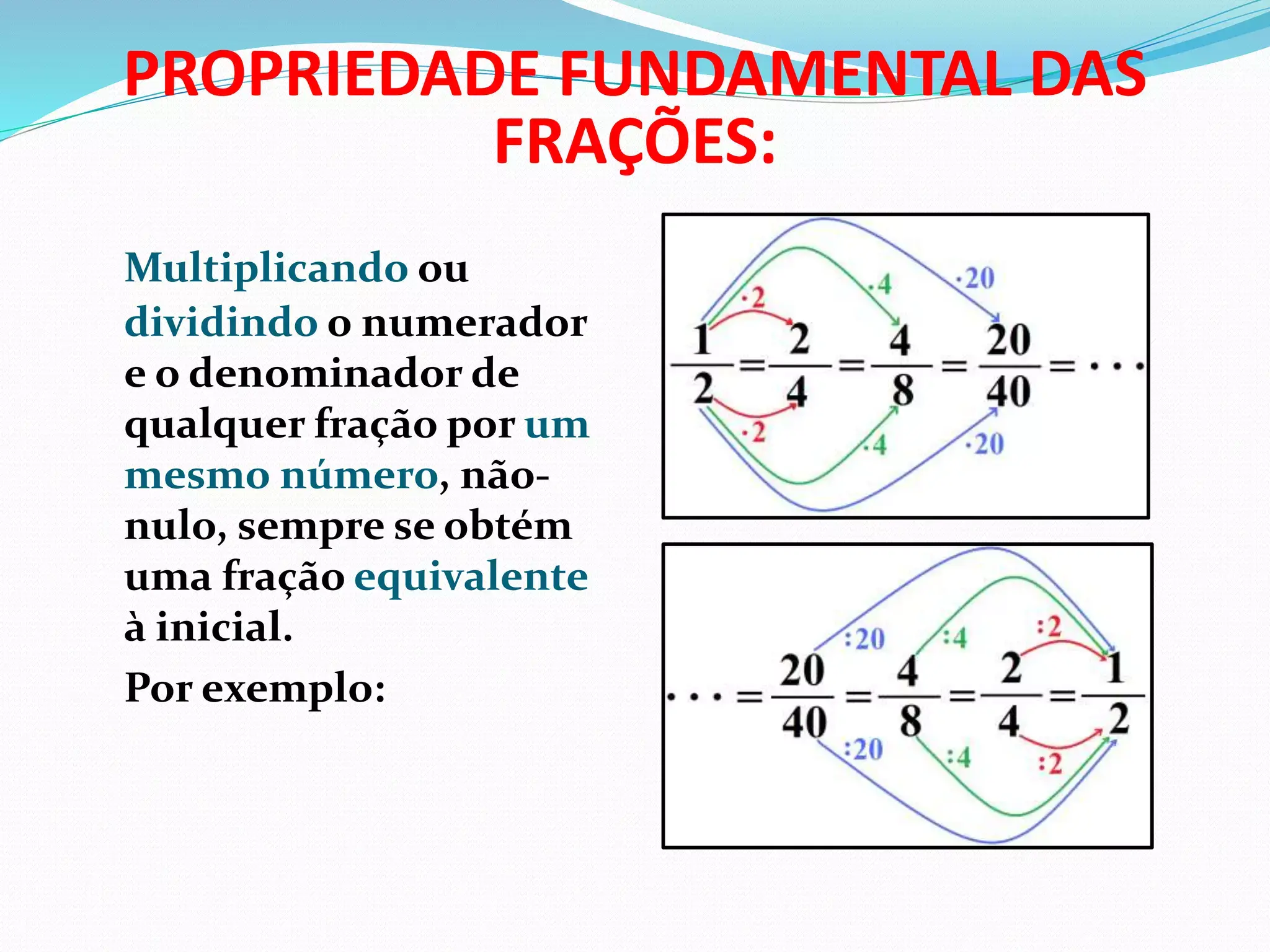
- Frações equivalentes têm o mesmo valor e permitem simplificar e comparar quantidades com segurança.
- Para somar/subtrair, use denominador comum (MMC); para dividir, multiplique pelo inverso.
- A forma irredutível é a versão mais simples; teste de equivalência: a·d = b·c.
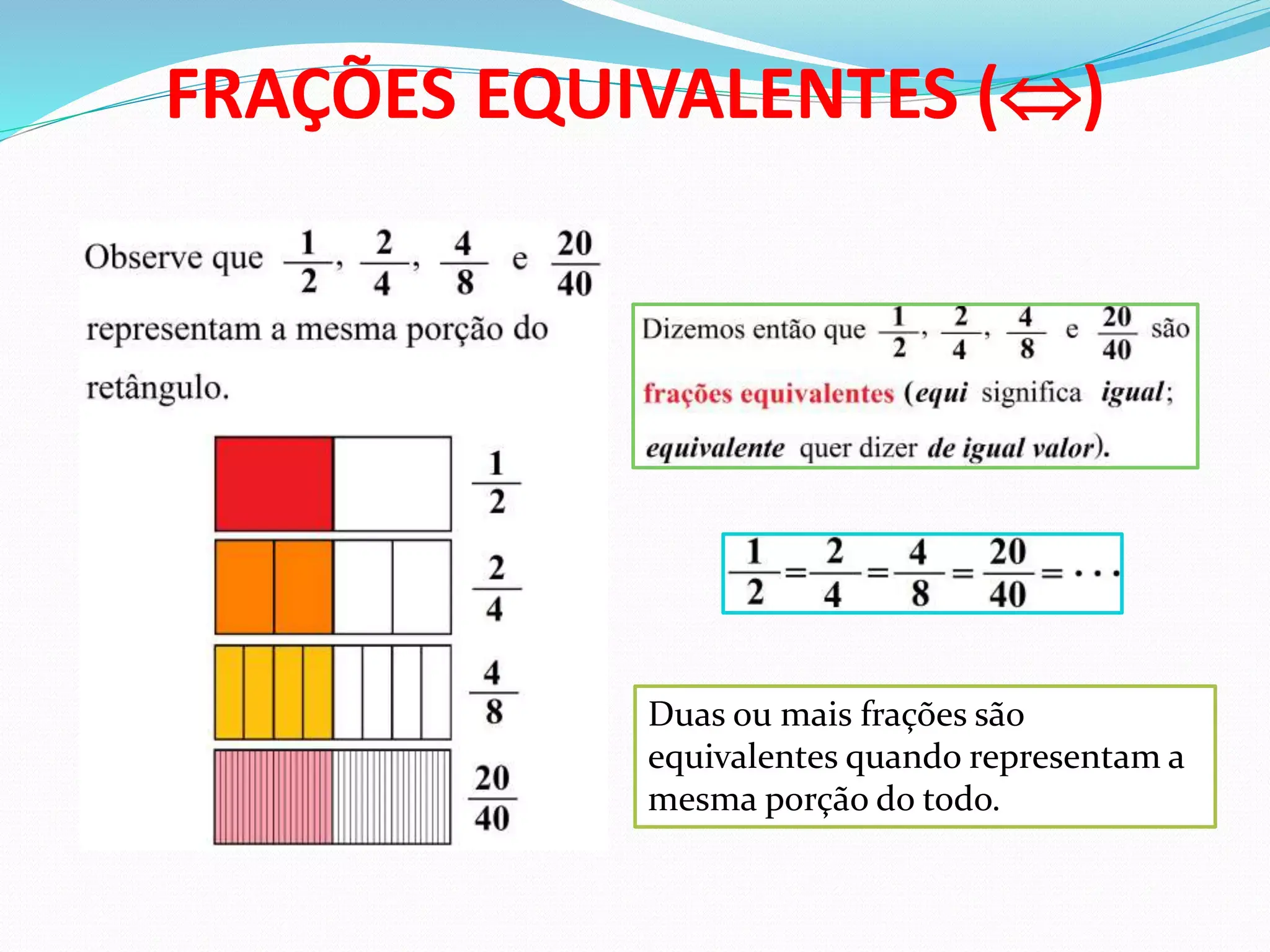
Entender frações é como ganhar um novo idioma para falar sobre partes de um todo, proporções e divisões do dia a dia. Seja em receitas, em gráficos, nas finanças ou na sala de aula, as frações equivalentes e não equivalentes aparecem a todo momento e são a base para operações e comparações matemáticas. Neste guia completo, você vai ver o que elas significam, como identificá-las, como ler e escrever frações corretamente, além de praticar com exemplos resolvidos.
Este conteúdo reúne explicações claras, exemplos práticos e conexões com outras áreas, como probabilidade, estatística, geometria, história da matemática e educação. Para tornar tudo ainda mais útil, você também verá regras essenciais como a verificação por “produto cruzado” (a·d = b·c), dicas para simplificar frações até a forma irredutível e quando usar o mínimo múltiplo comum (MMC) nas operações.
Pausa rápida para a publicidade — seguimos com o conteúdo completo a seguir!
O que é fração?
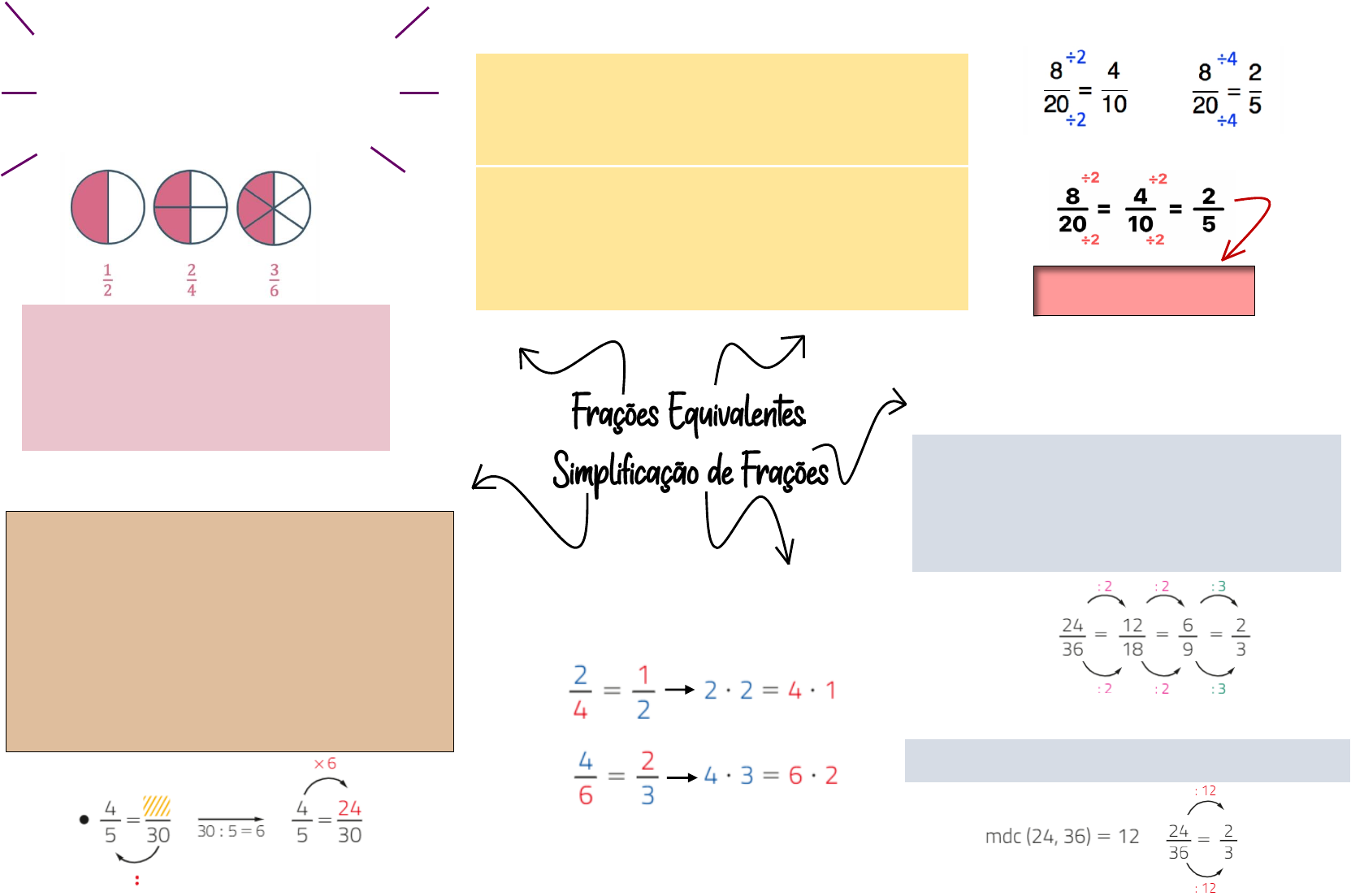
Fração é uma forma de escrever uma divisão entre dois números inteiros, representando quantas partes de um todo estamos considerando. Em a/b, o número de cima é o numerador (partes tomadas) e o de baixo é o denominador (em quantas partes iguais o todo foi dividido). Como fração representa uma divisão, a é o dividendo e b é o divisor, sendo indispensável que b ≠ 0.
Visualmente, dá para pensar em uma pizza, um retângulo ou qualquer figura dividida em partes iguais. Se você “pega” 3 de 8 pedaços, escreve 3/8: são três unidades de um total de oito. Essa leitura ajuda a enxergar a fração como parte do todo, o que é útil em receitas, escalas, gráficos e comparações.
Leitura e nomenclatura das frações
O denominador determina o “nome” da fração. O numerador é lido em sua forma cardinal (um, dois, três…), enquanto o denominador passa para a forma fracionária (meio, terço, quarto, quinto…). Assim, 3/5 é lido “três quintos” e 7/2 é “sete meios”.
A partir dos denominadores maiores que 10, a regra fica simples: adicionamos “avos” ao nome do número. Por exemplo, 13/20 é “treze vinte avos” e 4/11 é “quatro onze avos”. Para denominador 100, usamos “centésimos”, e para 1000, “milésimos”: 17/100 é “dezessete centésimos” e 9/1000 é “nove milésimos”.
Significados de numerador e denominador
O numerador indica a quantidade de partes consideradas, e o denominador indica em quantas partes iguais o todo está dividido. Em a/b, a é o que contamos e b é a referência do todo. Essa distinção evita erros comuns, como comparar frações apenas pelo numerador sem observar as “tamanhos” das partes.
Como a fração representa uma divisão, ela se relaciona diretamente com dividendo e divisor: a (numerador) é o dividendo e b (denominador) é o divisor. Jamais usamos denominador zero, pois não existe divisão por 0.
Tipos de fração
Fração própria
É a fração cujo numerador é menor que o denominador, representando uma quantidade menor que 1. Exemplos: 1/2, 3/4 e 12/100. Elas descrevem parcelas de um todo sem ultrapassar a unidade.
Fração imprópria
Ocorre quando o numerador é maior que o denominador, portanto representa valor maior que 1. Exemplos: 9/8, 7/2 e 25/12. Muitas vezes, convertemos frações impróprias em mistas para facilitar a interpretação.
Fração aparente
É a fração que equivale a um número inteiro, pois o numerador é divisível pelo denominador. Exemplos: 2/2 = 1, 8/4 = 2 e 9/3 = 3. Apesar de ter formato de fração, o valor final é inteiro.
Fração equivalente
Duas ou mais frações são equivalentes quando representam a mesma quantidade do todo, mesmo tendo numeradores e denominadores diferentes. Por exemplo, 1/2, 2/4 e 3/6 indicam a mesma metade. Esse conceito é crucial para simplificar, comparar e operar frações.
Fração irredutível
É a forma mais simples de uma fração, quando numerador e denominador não possuem divisor comum (além de 1). Exemplo clássico: 12/15 pode ser simplificada dividindo ambos por 3, chegando a 4/5. Como 4 e 5 não têm divisor comum maior que 1, 4/5 é irredutível. Outros exemplos de frações já irredutíveis: 7/8, 12/5 e 11/20.
Fração mista
Representa um número composto por uma parte inteira e uma parte fracionária, como 3 4/9 (três inteiros e quatro nonos). Outros exemplos: 9 3/4 e 2 1/3. É muito usada no cotidiano para medidas e receitas, pois comunica inteiros e “quebrados” de forma intuitiva.
Frações equivalentes: conceito, teste e simplificação
Frações equivalentes descrevem a mesma porção do todo ainda que escritas com números diferentes. Para gerar frações equivalentes, multiplique (ou divida) numerador e denominador pelo mesmo número não nulo. Exemplo: 1/2 → 2/4 → 3/6 → 50/100. Veja também frações equivalentes a 3/5.
Para verificar a equivalência entre a/b e c/d, aplique o produto cruzado: se a·d = b·c, então as frações são equivalentes. Exemplo: 1/3 e 2/6 — 1·6 = 6 e 3·2 = 6, logo são equivalentes.
Simplificar uma fração é encontrar uma equivalente com números menores, dividindo numerador e denominador por um mesmo fator comum. Quando nenhum fator maior que 1 divide ambos, atingimos a forma irredutível. Isso facilita operações e comparações.
A equivalência é a base para encontrar denominadores comuns ao somar ou subtrair frações diferentes. Muitas vezes, usamos o MMC (mínimo múltiplo comum) dos denominadores para reescrever as frações de modo que fiquem “compatíveis”.
Operações com frações
Adição e subtração com denominadores iguais
Quando os denominadores já são iguais, conservamos o denominador e operamos os numeradores. Exemplos: 3/5 + 1/5 = 4/5 e 5/7 − 3/7 = 2/7. É o caso mais simples e direto.
Adição e subtração com denominadores diferentes
Quando os denominadores são distintos, precisamos igualá-los. O caminho mais prático é encontrar o MMC dos denominadores e reescrever cada fração como uma equivalente com esse denominador comum. Depois, somamos ou subtraímos os numeradores.
Exemplo: 1/6 + 3/4. O MMC entre 6 e 4 é 12. Para 1/6 virar denominador 12, multiplicamos por 2: 1/6 = 2/12. Para 3/4 virar denominador 12, multiplicamos por 3: 3/4 = 9/12. Agora somamos: 2/12 + 9/12 = 11/12.
Multiplicação de frações
Multiplicar frações é multiplicar numerador por numerador e denominador por denominador. Exemplo: 3/5 · 4/7 = 12/35. Sempre que possível, simplifique antes ou depois da multiplicação para reduzir os números.
Divisão de frações
Para dividir uma fração pela outra, mantemos a primeira e multiplicamos pelo inverso da segunda. Exemplo: (3/5) ÷ (2/7) = 3/5 · 7/2 = 21/10. O inverso de c/d é d/c, desde que c e d sejam diferentes de 0.
Aplicações e conexões com outras áreas
Na culinária, frações equivalentes permitem ajustar receitas proporcionalmente: se a receita pede 1/2 xícara e você vai preparar metade, saber que 1/2 = 2/4 ajuda a manter as proporções corretas. Na prática, a equivalência evita desperdícios e garante o mesmo resultado.
Em finanças, frações e seus equivalentes facilitam comparar taxas e porcentagens. Por exemplo, 3/4 e 6/8 representam o mesmo retorno, o que ajuda a tomar decisões mais claras. Transformar fração em porcentagem ou decimal (1/4 = 0,25) também simplifica relatórios e análises.
Na física e na engenharia, frações aparecem em proporções e leis, como razões de grandezas e escalas em modelos. Mapas e maquetes usam escalas fracionárias, onde a equivalência garante relações consistentes entre medidas.
Em estatística e gráficos, frações comunicam partes de um total (setores de pizza, barras proporcionais). Métodos visuais, como pizzas e retângulos, tornam o conceito mais concreto, especialmente no ensino fundamental.
Na probabilidade, comparar chances com frações equivalentes é imediato: 1/5 e 2/10 têm a mesma probabilidade. Reconhecer equivalências acelera cálculos e interpretações em situações práticas.
A história da matemática mostra que frações acompanham a humanidade há milênios. Civilizações antigas, como egípcios e babilônios, já as utilizavam. Clássicos como Euclides discutiram proporções em Os Elementos, e matemáticos como Diofanto e al-Khwarizmi também contribuíram com ideias que ecoam no modo como entendemos frações hoje.
Na educação matemática, frações equivalentes são conteúdo central. Professores usam recursos visuais e, cada vez mais, tecnologia educacional para tornar a prática interativa. Softwares e aplicativos ajudam a treinar simplificação, MMC e operações de forma dinâmica.
Vocabulário essencial
- Frações: representação de uma parte de um todo por meio de numerador e denominador.
- Numerador: número que indica quantas partes do todo estão sendo consideradas.
- Denominador: número que mostra em quantas partes iguais o todo foi dividido.
- Equivalência: quando duas frações, mesmo diferentes na escrita, têm o mesmo valor.
- Frações equivalentes: frações que representam a mesma proporção do todo.
- Simplificar: reduzir a fração dividindo numerador e denominador por um mesmo fator.
- Denominador comum: denominador compartilhado que permite somar/subtrair frações.
- Receita: instruções culinárias que frequentemente usam medidas fracionárias.
- Investimento: aplicações financeiras que podem ser comparadas por frações e percentuais.
- Probabilidade: medida da chance de um evento, frequentemente expressa por frações.
- Cálculo: área avançada da matemática que se apoia em razões e frações.
- Teoria dos números: ramo que estuda propriedades dos inteiros e de relações como divisibilidade.
- Métodos visuais: diagramas e representações que ajudam a entender proporções.
- História da matemática: evolução dos conceitos numéricos e fracionários ao longo do tempo.
- Cultura: contextos sociais e históricos que influenciam o uso das frações.
- Educação matemática: campo dedicado ao ensino e aprendizagem de tópicos como frações.
Quadro rápido: ideias-chave sobre frações equivalentes
- Frações equivalentes representam o mesmo valor, ainda que escritas de forma diferente.
- Geramos equivalentes multiplicando ou dividindo numerador e denominador pelo mesmo número.
- 1/2 é equivalente a 2/4; em desenhos, essa igualdade aparece como “metade” do todo.
- Escalas de mapas/modelos e gráficos estatísticos usam equivalências para manter proporções.
- Podemos escrever equivalências como porcentagens (ex.: 1/4 = 25%) e decimais (0,25).
- O teste a·d = b·c decide se duas frações são equivalentes sem precisar desenhar.
Exemplos práticos e leitura de casos
Exemplo de equivalência por multiplicação: 2/3 → 4/6 (multiplicando ambos por 2). Valor igual, escrita diferente. Isso é útil para chegar a denominadores comuns na hora de somar ou subtrair.
Exemplo de simplificação: 18/24. Dividindo numerador e denominador por 6, obtemos 3/4. Se não houver mais fator comum, a fração está irredutível.
Exemplo de irredução “de cara”: 7/8. Como 7 é primo e não divide 8, já está na forma mais simples.
Exemplo de fração aparente: 12/4 = 3. A escrita é fracionária, mas o valor é inteiro. Isso ocorre sempre que o numerador for múltiplo exato do denominador.
Exercícios resolvidos
Questão 1
(IBFC 2022) Alicia guardou 3/10 do salário e pagou 1/10 com o aluguel. Que fração do salário sobrou?
- A) 1/10
- B) 3/10
- C) 4/10
- D) 6/10
Resolução: o salário foi “quebrado” em 10 partes. Foram usadas 3 + 1 = 4 partes; restam 10 − 4 = 6. Logo, sobrou 6/10 (alternativa D). É possível ainda simplificar 6/10 para 3/5 dividindo por 2 (frações equivalentes).
Questão 2
(Fundatec) Assinale a alternativa equivalente a 4/12.
- A) 3/12
- B) 1/3
- C) 6/12
- D) 12/4
- E) 1/4
Resolução: simplificando 4/12 por 4, temos 1/3. Portanto, a opção correta é 1/3 (alternativa B). Se preferir, também dá para checar com produto cruzado.
Dicas úteis e observações finais
Para somar e subtrair, pense primeiro nos denominadores: se forem iguais, vá direto ao ponto; se forem diferentes, encontre o MMC e reescreva as frações como equivalentes com denominador comum. Isso torna as contas mais organizadas.
Na multiplicação, simplifique o quanto puder antes ou depois do produto: isso evita números grandes e reduz erros. Na divisão, lembre-se: multiplicar pelo inverso da segunda fração resolve o problema rapidamente.
Valorize a forma irredutível: além de ser a “versão mais limpa” da fração, muitas respostas em provas e exercícios pedem o resultado simplificado. Treinar fatores comuns acelera esse processo.
Leituras complementares melhoram a fluência: revisar “macetes de divisão”, “transformação de fração em porcentagem” e “equivalência com decimais” ajuda a conectar conteúdos e a resolver problemas com mais segurança. Experimente também recursos visuais e videoaulas para fixar as ideias.
Dominar frações equivalentes e não equivalentes amplia a sua capacidade de comparar, calcular e comunicar quantidades em contextos reais. Do entendimento de numerador e denominador à leitura correta (de terços a milésimos), passando pelos tipos de fração, regras de equivalência, simplificação, MMC e operações, você tem agora um mapa completo para trabalhar com o tema com confiança em matemática, na escola e no cotidiano.