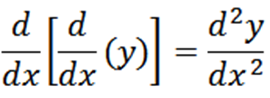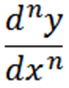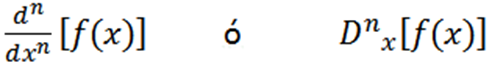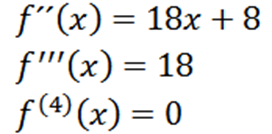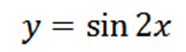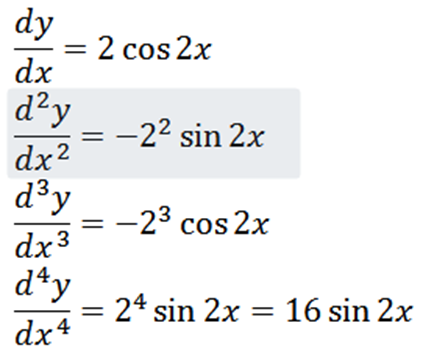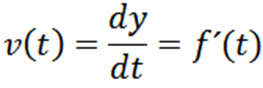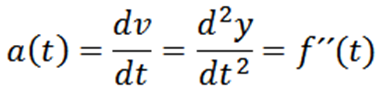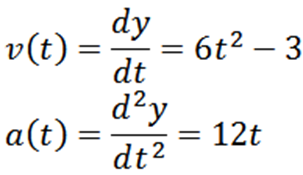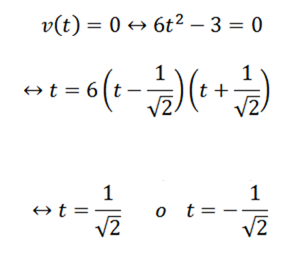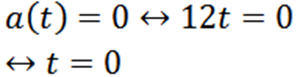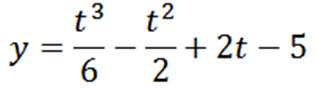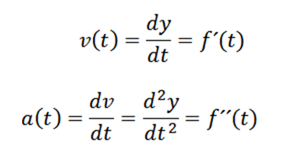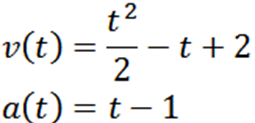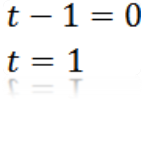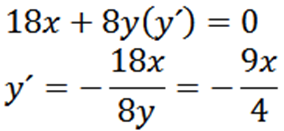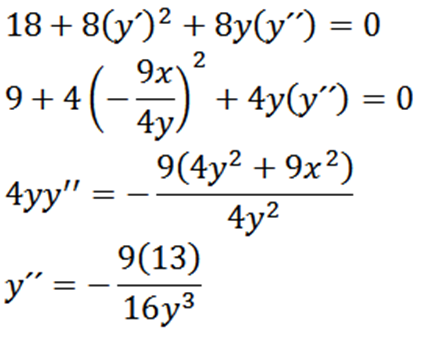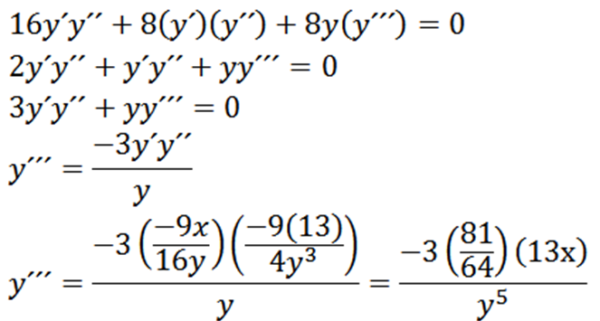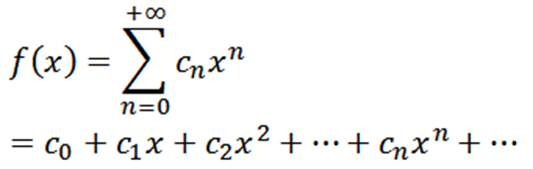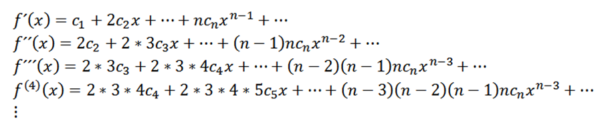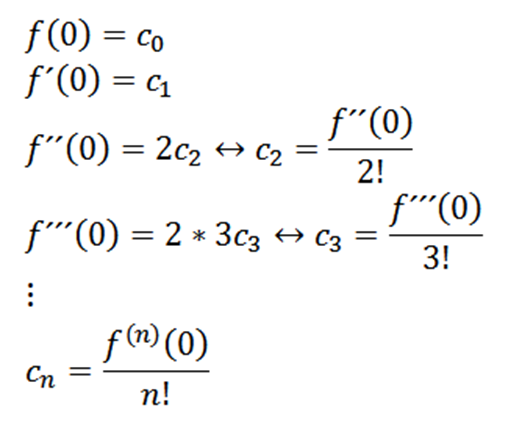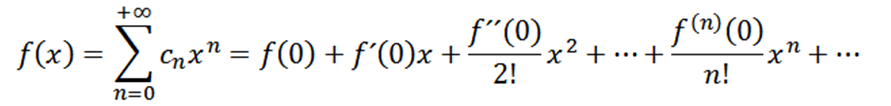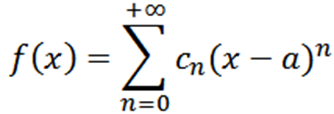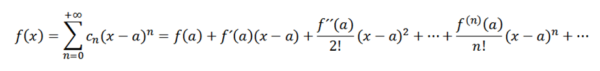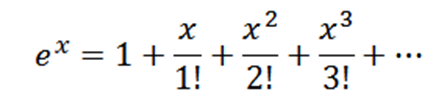Derivados sucessivos são derivadas de uma função que são obtidas a partir de derivadas anteriores. Ou seja, são as derivadas de derivadas. Esses conceitos são fundamentais no cálculo diferencial e são muito úteis para analisar o comportamento das funções em diferentes níveis de variação. Neste artigo, iremos explorar os derivados sucessivos, explicando como calculá-los e resolver alguns exercícios práticos para melhor compreensão do assunto.
Entendendo o conceito de derivadas sucessivas e sua importância no cálculo diferencial.
As derivadas sucessivas são um conceito fundamental no cálculo diferencial, utilizado para analisar o comportamento de funções em diferentes níveis de variação. Quando calculamos a derivada de uma função, estamos determinando sua taxa de variação instantânea em um ponto específico. No entanto, ao calcular derivadas sucessivas, estamos analisando como essa taxa de variação muda ao longo do tempo.
Para calcular as derivadas sucessivas de uma função, basta aplicar a regra da derivada sucessivamente, a partir da função original. Por exemplo, se temos uma função (f(x)) e calculamos sua primeira derivada (f'(x)), podemos calcular a segunda derivada (f”(x)) aplicando a regra da derivada novamente. Esse processo pode ser repetido para calcular derivadas de ordem superior, como a terceira derivada (f”'(x)) e assim por diante.
A importância das derivadas sucessivas no cálculo diferencial está relacionada à análise mais aprofundada do comportamento das funções. Ao estudar as derivadas de ordens superiores, podemos identificar pontos de inflexão, concavidade, máximos e mínimos locais, entre outras informações importantes sobre a função. Essas análises são essenciais em diversas áreas da matemática e da física, auxiliando no entendimento e na modelagem de fenômenos complexos.
Vamos agora resolver um exercício para exemplificar o cálculo de derivadas sucessivas:
Seja a função (f(x) = 3x^3 + 2x^2 – 5x + 7), vamos calcular a primeira e segunda derivada desta função.
1) Primeira derivada de (f(x)):
(f'(x) = 9x^2 + 4x – 5)
2) Segunda derivada de (f(x)):
(f”(x) = 18x + 4)
Com este exemplo, podemos ver como as derivadas sucessivas nos permitem analisar o comportamento de uma função de forma mais detalhada, fornecendo informações valiosas sobre sua curvatura, pontos críticos e tendências. Portanto, o estudo das derivadas sucessivas é essencial para quem deseja compreender o cálculo diferencial em sua totalidade.
Entenda as normas para derivar corretamente!
Quando estamos lidando com derivados sucessivos, é importante entender as normas para derivar corretamente. A derivada de uma função é a taxa de variação instantânea da função em relação a uma variável. Para derivar corretamente uma função, é necessário aplicar as regras de derivação de forma adequada.
Para derivar uma função composta, também conhecida como função derivada, é necessário aplicar a regra da cadeia. Essa regra consiste em derivar a função externa e, em seguida, multiplicar pela derivada da função interna.
Além disso, ao derivar uma função polinomial, é importante lembrar das regras básicas de derivação, como a regra do produto e a regra do quociente. É essencial praticar exercícios resolvidos para aprimorar suas habilidades de derivação.
Para ilustrar, vamos resolver um exercício simples de derivados sucessivos:
Exemplo: Calcular a derivada segunda da função ( f(x) = x^2 ).
Solução: Primeiramente, calculamos a primeira derivada da função ( f(x) ):
[ f'(x) = 2x ]
Em seguida, calculamos a segunda derivada da função:
[ f”(x) = frac{d}{dx}(2x) = 2 ]
Portanto, a derivada segunda da função ( f(x) = x^2 ) é ( 2 ).
Praticar exercícios de derivados sucessivos é fundamental para compreender as normas de derivação e aprimorar suas habilidades matemáticas. Lembre-se de sempre revisar as regras de derivação e praticar regularmente para obter sucesso na resolução de problemas de derivadas.
Tutorial simples para criar uma conta de derivada em poucos passos.
Para criar uma conta de derivada em poucos passos, siga as instruções abaixo:
Passo 1: Acesse o site da plataforma de derivados escolhida e clique em “Criar conta”.
Passo 2: Preencha os campos requeridos com suas informações pessoais, como nome, e-mail e senha.
Passo 3: Após preencher os campos, clique em “Enviar” ou “Criar conta” para finalizar o processo.
Agora que você criou sua conta de derivada, pode começar a explorar e negociar diferentes ativos financeiros.
Derivados Sucessivos (com Exercícios Resolvidos)
Os derivados sucessivos são operações matemáticas que envolvem a derivada de uma função derivada. Para calcular derivados sucessivos, basta aplicar a regra da derivada múltipla várias vezes.
Por exemplo, se tivermos a função f(x) = 3x^2 + 2x – 1, podemos calcular a primeira derivada (f'(x)) e a segunda derivada (f”(x)) da seguinte forma:
Passo 1: Calcule a primeira derivada de f(x): f'(x) = 6x + 2.
Passo 2: Calcule a segunda derivada de f(x): f”(x) = 6.
Assim, os derivados sucessivos da função f(x) seriam f'(x) = 6x + 2 e f”(x) = 6.
Praticar a resolução de exercícios envolvendo derivados sucessivos é essencial para a compreensão e domínio desses conceitos matemáticos.
Significado e cálculo da derivada de uma constante na matemática básica.
A derivada de uma constante na matemática básica é sempre igual a zero. Isso ocorre porque a derivada representa a taxa de variação de uma função em relação a uma variável, e uma constante não varia.
Para calcular a derivada de uma constante, basta lembrar que a derivada de uma constante é sempre zero. Por exemplo, se temos uma função f(x) = 5, a derivada de f(x) em relação a x é igual a zero.
Derivados Sucessivos (com Exercícios Resolvidos)
Os derivados sucessivos representam a derivada de uma função derivada. Ou seja, se temos uma função f(x) e calculamos a derivada de f(x), obtemos uma nova função g(x). Se calculamos a derivada de g(x), obtemos uma nova função h(x), e assim por diante.
Vamos resolver um exercício para exemplificar os derivados sucessivos:
Seja f(x) = 3x^2 + 4x – 2. Calcularemos a primeira e a segunda derivada de f(x).
Primeira derivada de f(x):
f'(x) = d/dx(3x^2) + d/dx(4x) – d/dx(2)
f'(x) = 6x + 4 – 0
f'(x) = 6x + 4
Segunda derivada de f(x):
f”(x) = d/dx(6x) + d/dx(4)
f”(x) = 6 – 0
f”(x) = 6
Neste exemplo, calculamos a primeira e a segunda derivada da função f(x). Os derivados sucessivos são úteis para analisar a taxa de variação de uma função em relação a sua variável independente.
Derivados Sucessivos (com Exercícios Resolvidos)
Os derivados sucessivas são os derivados de uma função após a segunda derivada. O processo para calcular derivadas sucessivas é o seguinte: existe uma função f, que podemos derivar e, assim, obter a função derivada f ‘. À referida derivada de f, podemos derivá-la novamente, obtendo (f ‘)’.
Essa nova função é chamada de segunda derivada; todos os derivativos calculados a partir do segundo são sucessivos; Estes, também chamados de ordem superior, têm ótimas aplicações, como fornecer informações sobre o gráfico do gráfico de uma função, o teste da segunda derivada para extremos relativos e a determinação de séries infinitas.
Definição de
Usando a notação de Leibniz, temos que a derivada de uma função “y” em relação a “x” é dy / dx. Para expressar a segunda derivada de “e” usando a notação de Leibniz, escrevemos da seguinte maneira:
Em geral, podemos expressar derivadas sucessivas da seguinte forma com a notação de Leibniz, em que n representa a ordem da derivada.
Outras notações usadas são as seguintes:
Alguns exemplos em que podemos ver as diferentes notações são:
Exemplo 1
Obtenha todas as derivadas da função f definidas por:
Usando as técnicas usuais de derivação, temos que a derivada de f é:
Repetindo o processo, podemos obter a segunda derivada, a terceira derivada e assim por diante.
Observe que a quarta derivada é zero e a derivada de zero é zero, então temos que:
Exemplo 2
Calcule a quarta derivada da seguinte função:
Derivando a função fornecida, temos como resultado:
Velocidade e aceleração
Uma das motivações que levaram à descoberta da derivada foi a busca pela definição de velocidade instantânea. A definição formal é a seguinte:
Seja y = f (t) uma função cujo gráfico descreve a trajetória de uma partícula em um instante t , então sua velocidade em um instante t é dada por:
Uma vez que a velocidade de uma partícula é obtida, podemos calcular a aceleração instantânea, definida da seguinte forma:
A aceleração instantânea de uma partícula cuja trajetória é dada por y = f (t) é:
Exemplo 1
Uma partícula se move em uma linha de acordo com a função de posição:
Onde “y” é medido em metros e “t” em segundos.
– Em que momento é a velocidade 0?
– Em que momento é a aceleração 0?
Ao derivar a função de posição «e», temos que sua velocidade e aceleração são dadas respectivamente por:
Para responder à primeira pergunta, basta determinar quando a função v é zerada; isto é:
Prosseguimos com a seguinte pergunta analogamente:
Exemplo 2
Uma partícula se move em uma linha de acordo com a seguinte equação de movimento:
Determine “t, y” e “v” quando a = 0.
Sabendo que velocidade e aceleração são dadas por
Procuramos obter e obter:
Fazendo a = 0, temos:
De onde podemos deduzir que o valor de t igual a zero é t = 1.
Então, avaliando em t = 1 a função de posição e a função de velocidade, temos que:
Aplicações
Derivação explícita
Derivadas sucessivas também podem ser obtidas por derivação implícita.
Exemplo
Dada a seguinte elipse, encontre «e»:
Derivando implicitamente em relação a ax, temos:
Então, derivar implicitamente em relação ao machado, nos dá:
Finalmente, temos:
Extremidades relativas
Outro uso que podemos dar às derivadas de segunda ordem é no cálculo dos fins relativos de uma função.
O critério da primeira derivada para extremos locais nos diz que, se tivermos uma função contínua f em um intervalo (a, b) e houver um c que pertença a esse intervalo, que será anulado em c (ou seja, c é um ponto crítico), um desses três casos pode ocorrer:
– Se f ‘(x)> 0 para qualquer x pertencente a (a, c) ef’ (x) <0 para x pertencente a (c, b), então f (c) é um máximo local.
– Se f ‘(x) <0 para qualquer x pertencente a (a, c) ef’ (x)> 0 para x pertencente a (c, b), então f (c) é um mínimo local.
– Se f´ (x) tem o mesmo sinal em (a, c) e em (c, b), isso implica que f (c) não é um fim local.
Usando o critério da segunda derivada, podemos saber se um número crítico de uma função é um máximo ou mínimo local, sem ter que ver qual é o sinal da função nos intervalos mencionados acima.
O segundo critério de deriva nos diz que se f´ (c) = 0 e que f´´ (x) é contínuo em (a, b), acontece que se f´´ (c)> 0 então f (c) é um mínimo local e se f´´ (c) <0, então f (c) é um máximo local.
Se f´´ (c) = 0, não podemos concluir nada.
Exemplo
Dada a função f (x) = x 4 + (4/3) x 3 – 4x 2 , encontre os máximos e mínimos relativos de f aplicando os critérios da segunda derivada.
Primeiro calculamos f´ (x) ef´´ (x) e temos:
f´ (x) = 4x 3 + 4x 2 – 8x
f´´ (x) = 12x 2 + 8x – 8
Agora, f´ (x) = 0 se, e somente se 4x (x + 2) (x – 1) = 0, e isso ocorre quando x = 0, x = 1 ox = – 2.
Para determinar se os números críticos obtidos são extremos relativos, basta avaliar em f´´ e assim observar seu sinal.
f´´ (0) = – 8, então f (0) é um máximo local.
f´´ (1) = 12, então f (1) é um mínimo local.
f´´ (- 2) = 24, então f (- 2) é um mínimo local.
Taylor series
Seja f uma função definida da seguinte forma:
Esta função possui um raio de convergência R> 0 e possui derivadas de todas as ordens em (-R, R). Derivadas sucessivas de f nos fornecem:
Tomando x = 0, podemos obter os valores de c n com base em suas derivadas da seguinte maneira:
Se tomarmos um = 0 como a função f (ou seja, f ^ 0 = f), podemos reescrever a função da seguinte maneira:
Agora considere a função como uma série de potências em x = a:
Se realizarmos uma análise análoga à anterior, devemos escrever a função f como:
Essas séries são conhecidas como séries de Taylor de f em a. Quando a = 0, temos o caso específico chamado série Maclaurin. Esse tipo de série é de grande importância matemática, especialmente na análise numérica, pois, graças a isso, podemos definir funções em computadores como e x , sen (x) e cos (x).
Exemplo
Obtenha a série Maclaurin para e x .
Observe que se f (x) = e x , então f (n) (x) = e x ef (n) (0) = 1, então sua série Maclaurin é:
Referências
- Frank Ayres, J. & Mendelson, E. (sf). Cálculo 5ed. Mc Graw Hill
- Leithold, L. (1992). O CÁLCULO com Geometria Analítica. HARLA, SA
- Purcell, EJ, Varberg, D. & Rigdon, SE (2007). Cálculo México: Pearson Education.
- Saenz, J. (2005). Cálculo diferencial. Hipotenusa
- Saenz, J. (sf). Cálculo integral. Hipotenusa