O balanço da matéria é a contagem dos componentes que pertencem a um sistema ou processo em estudo. Essa balança pode ser aplicada a praticamente qualquer tipo de sistema, pois é assumido que a soma das massas de tais elementos deve permanecer constante em diferentes momentos de medição.
Mármores, bactérias, animais, madeira, ingredientes para um bolo podem ser entendidos como um componente; e no caso de química, moléculas ou íons, ou mais especificamente, compostos ou substâncias. Então, a massa total das moléculas que entram no sistema, com ou sem reação química, deve permanecer constante; desde que não haja perdas de vazamento.

Na prática, existem inúmeros problemas que podem afetar o equilíbrio da matéria, além de levar em consideração vários fenômenos da matéria e o efeito de muitas variáveis (temperatura, pressão, vazão, agitação, tamanho do reator etc.).
No papel, no entanto, os cálculos do saldo da matéria devem corresponder; isto é, a massa dos compostos químicos não deve desaparecer a qualquer momento. Fazer esse equilíbrio é análogo a colocar uma pilha de pedras em equilíbrio. Se uma das massas sai de lugar, tudo desmorona; Nesse caso, isso significaria que os cálculos estão errados.
Equação geral do balanço de matéria
Em qualquer sistema ou processo, suas bordas devem ser definidas primeiro. A partir deles, será conhecido quais compostos entram ou saem. É conveniente fazê-lo, especialmente se houver várias unidades de processo a serem consideradas. Quando todas as unidades ou subsistemas são considerados, fala-se de um equilíbrio geral da matéria.
Essa balança possui uma equação que pode ser aplicada a qualquer sistema que obedeça à lei de conservação de massa. A equação é a seguinte:
E + G – S – C = A
Onde E é a quantidade de matéria que entra no sistema; G é o que é gerado se uma reação química ocorrer no processo (como em um reator); S é o que sai do sistema; C é o que é consumido , novamente, se houver uma reação; e, finalmente, A é o que se acumula .
Simplificação
Se não houver reação química no sistema ou processo em estudo , G e C valerão zero. Assim, a equação é como:
E – S = A
Se o sistema também é considerado estacionário, sem alterações consideráveis nas variáveis ou fluxos dos componentes, diz-se que nada se acumula no interior. Portanto, A é zero e a equação acaba sendo mais simplificada:
E = S
Ou seja, a quantidade de matéria que entra é igual à que sai. Nada pode se perder ou desaparecer.
Por outro lado, se houver uma reação química, mas o sistema estiver em estado estacionário, G e C terão valores e A permanecerá zero:
E + G – S – C = 0
E + G = S + C
Significando que em um reator a massa dos reagentes que entram e os produtos que geram nele é igual à massa dos produtos e reagentes que saem e dos reagentes consumidos.
Exemplo de uso: peixe no rio
Suponha que você esteja estudando o número de peixes em um rio, cujas margens representam a fronteira do sistema. Sabe-se que, em média, 568 peixes entram por ano, 424 nascem (geram), 353 morrem (consomem) e 236 migram ou saem.
Aplicando a equação geral, você tem:
568 + 424 – 353 – 236 = 403
Isso significa que, por ano, 403 peixes se acumulam no rio; isto é, por ano o rio é enriquecido mais com peixes. Se A tivesse um valor negativo, isso significaria que o número de peixes está diminuindo, talvez com impactos ambientais negativos.
Tipos
A partir da equação geral, pode-se pensar que existem quatro equações para diferentes tipos de processos químicos. No entanto, o balanço da matéria é dividido em dois tipos, de acordo com outro critério: o tempo.
Saldo diferencial
No balanço de matéria diferencial, a quantidade de componentes dentro de um sistema é dada em um determinado momento ou momento. Tais quantidades de massa são expressas com unidades de tempo e, portanto, representam velocidades; por exemplo, Kg / h, indicando quantos quilômetros entram, saem, acumulam, geram ou consomem em uma hora.
Para que haja fluxos de massa (ou volumétricos, com densidade em mãos), o sistema geralmente deve estar aberto.
Balanço abrangente
Quando o sistema é fechado, como ocorre com as reações realizadas em reatores intermitentes (tipo batelada), as massas de seus componentes geralmente ficam mais interessadas antes e depois do processo; isto é, entre os tempos inicial e final t.
Portanto, as quantidades são expressas como meras massas e não velocidades. Esse tipo de equilíbrio é feito mentalmente quando se usa um liquidificador: a massa dos ingredientes que entram deve ser igual ao que resta depois de desligar o motor.
Exemplo de exercício
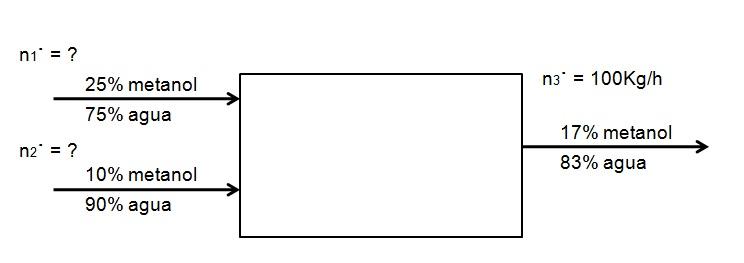
É desejável diluir um fluxo de uma solução de 25% de metanol em água, com outro de uma concentração de 10%, mais diluída, de modo que sejam gerados 100 kg / h de uma solução de 17% de metanol. Quanto de ambas as soluções de metanol, em 25 e 10%, deve entrar no sistema por hora para conseguir isso? Suponha que o sistema esteja em estado estacionário
O diagrama a seguir exemplifica a instrução:
Como não há reação química, a quantidade de metanol que entra deve ser igual à que sai:
E Metanol = S Metanol
0,25 N 1 · + 0,10 N 2 · = 0,17 N 3 ·
Somente o valor de n 3 · é conhecido . O resto é desconhecido. Para resolver essa equação de duas incógnitas, é necessário outro equilíbrio: o da água. Fazendo o mesmo equilíbrio para a água, você tem:
0,75 N 1 · + 0,90 N 2 · = 0,83 N 3 ·
O valor de n 1 · é limpo para a água (também pode ser n 2 · ):
n 1 · = (83 Kg / h – 0,90n 2 · ) / (0,75)
Substituindo n 1 · na equação do balanço da matéria para o metanol e resolvendo n 2 · você tem:
0,25 [(83 kg / h – 0,90n 2 · ) / (0,75)] + 0,10 n 2 · = 0,17 (100 kg / h)
n 2 · = 53,33 kg / h
E para obter n 1 · basta subtrair:
n 1 · = (100-53,33) Kg / h
= 46,67 Kg / h
Portanto, 46,67 kg de solução a 25% de metanol e 53,33 kg da solução a 10% devem entrar no sistema por hora.
Referências
- Felder e Rousseau. (2000) Princípios elementares de processos químicos. (Segunda edição.) Addison Wesley
- Fernández Germán. (20 de outubro de 2012). Definição de equilíbrio de matéria. Recuperado de: Industriaquimica.net
- Balanços da matéria: processos industriais I. [PDF]. Recuperado de: 3.fi.mdp.edu.ar
- Faculdade Regional da UNT La Plata. (sf). Equilíbrio da matéria [PDF]. Recuperado de: frlp.utn.edu.ar
- Gómez Claudia S. Quintero. (sf). Balanços da matéria. [PDF]. Recuperado de: webdelprofesor.ula.ve