- La pressione osmotica dipende dal numero di particelle in soluzione: π = M·R·T (molecolari) e π = M·R·T·i (ioniche).
- Il fattore di Van’t Hoff i e, se serve, il grado di ionizzazione α determinano l’aumento di particelle e quindi di π.
- Applicazioni cruciali: soluzioni isotoniche in medicina e osmosi inversa per la dissalazione dell’acqua.

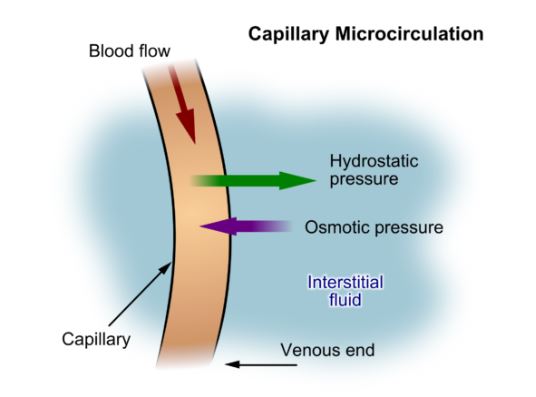
La pressione osmotica è la spinta minima che bisogna applicare a una soluzione concentrata per evitare che il solvente fluisca spontaneamente attraverso una membrana semipermeabile dal lato meno concentrato a quello più concentrato. In parole semplici: se due soluzioni sono separate da una membrana che lascia passare solo il solvente, il solvente tende a muoversi verso la zona più “ricca” di soluto; la pressione osmotica è il valore che blocca questo flusso.
Si tratta di una proprietà colligativa, cioè dipende esclusivamente dal numero di particelle di soluto presenti e non dalla loro natura chimica. Questo spiega perché soluzioni con uguale concentrazione molare ma con soluti che generano numeri diversi di particelle in acqua (per esempio molecole neutre vs ioni) esibiscono pressioni osmotiche differenti.
Osmosi e definizione operativa di pressione osmotica
L’osmosi è il passaggio netto del solvente attraverso una membrana semipermeabile dal comparto ipotonico (meno concentrato in soluto) al comparto ipertonico (più concentrato), finché le forze in gioco portano all’equilibrio. Immagina un tubo a U separato da una membrana: a sinistra solo acqua, a destra una soluzione. Con il tempo il livello del lato destro sale finché la differenza di altezza (quindi di pressione idrostatica) equilibra la tendenza al flusso osmotico.
La pressione osmotica π è quindi la pressione esterna che, se applicata sul lato della soluzione più concentrata, impedisce in partenza l’ingresso del solvente. Non appena la pressione applicata uguaglia la pressione osmotica della soluzione, il flusso osmotico si arresta.
Perché la pressione osmotica è una proprietà colligativa
Le proprietà colligative dipendono dal numero totale di particelle in soluzione, non dal tipo. Per questo, a parità di molarità, una soluzione ionica (che si dissocia in ioni) produce più particelle rispetto a una soluzione molecolare (le cui molecole restano integre), e dunque mostra una pressione osmotica maggiore.
Classificazione in base alla pressione osmotica. Due soluzioni separate da una membrana possono essere: isotoni (stessa pressione osmotica), ipertoniche (quella con pressione osmotica maggiore) o ipotoniche (quella con pressione osmotica minore). Questa distinzione è centrale in biologia e medicina: soluzioni isotoniche rispetto al sangue evitano rigonfiamenti o collassi delle cellule.
Esempio biologico: il siero fisiologico è formulato per avere pressione osmotica simile a quella del sangue (circa 7,7–7,8 atm), così da non far “gonfiare” o “raggrinzire” i globuli rossi. Se fosse ipertonico, le cellule perderebbero acqua; se fosse ipotonico, assorbirebbero acqua fino a rischio di emolisi.
Equazione di Van’t Hoff e analogia con i gas ideali
Jacobus Henricus Van’t Hoff notò che la pressione osmotica obbedisce a una legge formale simile a quella dei gas ideali. A partire da PV = nRT e dalla definizione di molarità M = n/V, si ottiene per soluzioni ideali (diluite):
π = M · R · T
Significato dei simboli: M è la molarità in mol·L-1, R la costante universale dei gas, T la temperatura assoluta in Kelvin. Per R si usano comunemente due valori numerici equivalenti: 0,082 atm·L·mol-1·K-1 oppure 62,3 mmHg·L·mol-1·K-1. Entrambi sono corretti, basta coerenza nelle unità.
Soluzioni ioniche: fattore di Van’t Hoff i. Se il soluto si dissocia in ioni, il numero di particelle in soluzione aumenta. Per tenerne conto si introduce i (fattore di Van’t Hoff), pari al rapporto tra particelle finali e particelle iniziali. In tal caso:
π = M · R · T · i
Soluzioni molecolari vs soluzioni ioniche: cosa cambia davvero
Soluzioni molecolari (per esempio zuccheri come saccarosio o glucosio) non danno ioni in acqua: il numero di particelle rimane quello iniziale. In questi casi, π = M · R · T descrive il fenomeno in modo diretto.
Esempio saccarosio. Considera una soluzione 1,0 mol·L-1 di saccarosio a 0 °C (T = 273 K). Usando R = 0,082 atm·L·mol-1·K-1:
π = (1,0) · (0,082) · (273) ≈ 22,4 atm. In una soluzione molecolare le molecole si separano l’una dall’altra ma non si ionizzano, quindi le particelle totali non aumentano.
Soluzioni ioniche (acidi forti, basi forti, sali solubili) si dissociano in ioni e incrementano il numero di particelle. Per esempio, HCl(aq) dà H+ e Cl–, cioè da 1 “unità” iniziale si passa a 2 particelle: in condizioni ideali i = 2. Similmente, FeBr3 genera Fe3+ + 3 Br– (quattro particelle totali), dunque i = 4.
Conseguenza immediata: a parità di M e T, una soluzione ionica ha π più elevata di una molecolare perché il numero di particelle è maggiore. Più particelle significa maggiore tendenza osmotica e, quindi, più pressione necessaria per impedirla.
Esempi numerici chiave (passo dopo passo)
1) Glucosio 0,30 M a 37 °C. Il glucosio è molecolare (i = 1). Dati: M = 0,30 mol·L-1, T = 37 °C = 310 K, R = 0,082 atm·L·mol-1·K-1.
π = M · R · T = 0,30 · 0,082 · 310 ≈ 7,63 atm. Questo valore è spesso citato perché risulta vicino alla pressione osmotica del sangue nei calcoli didattici.
2) HCl 1,0 M a 0 °C. Considerando ionizzazione completa (i = 2):
π = M · R · T · i = 1,0 · 0,082 · 273 · 2 ≈ 44,8 atm. Il raddoppio delle particelle rispetto al caso molecolare raddoppia π alla stessa concentrazione e temperatura.
3) FeBr3 1,0 M a 0 °C. Essendo i = 4:
π = 1,0 · 0,082 · 273 · 4 ≈ 89,6 atm. Più ioni generati dal soluto, più alto il valore di π.
4) NaCl vs Ca3(PO4)2 entrambi 1,0 M. NaCl → Na+ + Cl– (i = 2). Ca3(PO4)2 → 3 Ca2+ + 2 PO43- (i = 5). A parità di M e T, la soluzione di fosfato tricalcico avrà π più elevata perché crea 5 particelle per formula unit contro 2 del cloruro di sodio.
5) Acqua di mare (NaCl 0,40 M) a 27 °C. Trascurando altri soluti e assumendo i = 2 (dissociazione completa), T = 300 K, R = 0,082 atm·L·mol-1·K-1:
π = 0,40 · 0,082 · 300 · 2 ≈ 19,7 atm. Ciò indica che per inversione osmotica (osmosi inversa) serve applicare una pressione superiore a ~19,7 atm per spingere il solvente dal lato più concentrato a quello meno concentrato e ottenere dissalazione.
6) Determinazione della massa molare della emoglobina. Una soluzione di emoglobina si prepara sciogliendo 1,0 g in 0,10 L di solvente. A 20 °C (293 K) si misura π = 2,75 mmHg. Con R = 62,3 mmHg·L·mol-1·K-1, per soluzioni molecolari vale: π = M · R · T, con M = m/(Mm·V). Da cui: Mm = m · R · T / (π · V).
Sostituendo: Mm = (1,0 g) · (62,3) · (293) / (2,75 · 0,10) ≈ 6,7 · 104 g·mol-1. Il risultato rientra negli ordini di grandezza attesi per una macromolecola proteica.
7) Effetto del grado di ionizzazione (α) su i. Se l’elettrolita non è completamente dissociato, il fattore i si calcola con i = 1 + α (q – 1), dove q è il numero di ioni generati per formula unit a dissociazione completa. Per HCl (q = 2), con α = 0,914:
i = 1 + 0,914 (2 – 1) = 1,914.
Esempio numerico: 1,825 g di HCl in 0,50 L a 293 K, R = 0,082 atm·L·mol-1·K-1. Le moli sono n = m/Mr = 1,825/36,5 ≈ 0,050 mol; Molarità M = n/V = 0,050/0,50 = 0,10 M. Quindi:
π = M · R · T · i = 0,10 · 0,082 · 293 · 1,914 ≈ 4,6 atm. La dissociazione incompleta riduce π rispetto al caso ideale i = 2.
8) Cambio di unità: usare kPa al posto di atm. A volte si usa R = 8,3 kPa·L·mol-1·K-1. Per NaCl 0,15 M a 37 °C (310 K) con i = 2:
π = 0,15 · 8,3 · 310 · 2 ≈ 771,9 kPa. Con unità coerenti, il valore numerico cambia ma la fisica resta identica.
Approfondimenti pratici e casi didattici ricorrenti
Soluzioni isotoniche a confronto. Se due soluzioni hanno la stessa π alla medesima T, sono isotoniche. Questo concetto è sfruttato per confrontare direttamente concentrazioni molari “effettive” quando siano presenti elettroliti (cioè M effettiva = M · i).
Roland dei calcoli rapidi. Per stime a colpo d’occhio: raddoppiare M o T raddoppia π, mentre raddoppiare i produce lo stesso effetto (a parità degli altri parametri). Così è facile prevedere come varia π senza rifare tutta la moltiplicazione.
U-tube: lettura fisica. Nel classico tubo a U, il dislivello h tra i due bracci crea una pressione idrostatica ρ g h che controbilancia il “richiamo” osmotico. Applicando dall’alto una pressione esterna pari a π si blocca il flusso prima che il dislivello si crei.
Effetti dell’elettrolita “multicarica”. Sali come Ca3(PO4)2 generano molte particelle. All’aumentare di q (numero totale di ioni), i cresce e così pure la pressione osmotica per la stessa M. Questo spiega perché, a molarità uguale, alcuni sali “pesano” di più sulle proprietà colligative.
Limiti del modello e condizioni di validità
La relazione di Van’t Hoff vale al meglio per soluzioni diluite e ideali. A concentrazioni elevate, interazioni tra ioni e solvente, associazioni/complessazioni e attività diverse dalle concentrazioni possono introdurre deviazioni non trascurabili.
Temperatura in Kelvin, sempre. Dato che R è definita in Kelvin, l’uso di T assoluta è obbligatorio. Dimenticarlo è tra gli errori più comuni nei problemi di chimica-fisica delle soluzioni.
Scelta di R e coerenza delle unità. Se si lavora in atm, usare 0,082 atm·L·mol-1·K-1. Se si usano mmHg, preferire 62,3 mmHg·L·mol-1·K-1. In kPa, 8,3 kPa·L·mol-1·K-1. Mai mescolare sistemi di unità senza conversioni.
Dissociazione parziale e grado di ionizzazione. Elettroliti deboli (o condizioni non ideali) richiedono di valutare α e calcolare i con i = 1 + α(q – 1). In laboratorio o in esercizi, questo passaggio evita di sovrastimare π.
Implicazioni biologiche e applicazioni tecnologiche
In fisiologia, l’equilibrio osmotico è vitale. Le cellule mantengono l’omeostasi regolando l’ingresso/uscita d’acqua. Un mezzo esterno ipertonico “tira fuori” acqua (cellule che si raggrinziscono); uno ipotonico la “spinge dentro” (cellule che si gonfiano). Per il sangue, valori tipici di π sono attorno a 7,7–7,8 atm; vedi anche pressione oncotica, guida pratica per infusioni isotoniche.
Osmosi inversa (reverse osmosis, RO). Applicando una pressione superiore a π sul lato concentrato, si inverte il flusso naturale del solvente e lo si forza a passare verso il lato diluito, separandolo dal soluto. È il principio alla base della dissalazione dell’acqua di mare e di numerosi impianti di potabilizzazione.
Emodialisi e medicina. Nella dialisi si sfruttano membrane semipermeabili per rimuovere scorie metaboliche e regolare il bilancio idrico. Anche se i dettagli includono diffusione e ultrafiltrazione, la logica di selettività e controllo di pressione osmotica resta un caposaldo per evitare squilibri cellulari durante il trattamento.
Ricerca e biochimica. La misura di π consente di stimare masse molari di macromolecole (proteine, polimeri) a basse concentrazioni, come visto per l’emoglobina. È una via sperimentale elegante per indagare dimensione e comportamento in soluzione.
Riepilogo operativo: formule, dati e trucchi
Formule fondamentali:
• Soluzioni molecolari: π = M · R · T
• Soluzioni ioniche: π = M · R · T · i
• Grado di ionizzazione: i = 1 + α (q – 1)
• Relazione con molarità e massa: M = m / (Mm · V) e, quindi, Mm = m · R · T / (π · V)
Valori utili di R (scegli in base alle unità):
• 0,082 atm·L·mol-1·K-1
• 62,3 mmHg·L·mol-1·K-1
• 8,3 kPa·L·mol-1·K-1
Consiglio pratico: imposta subito le unità desiderate e mantienile fino al risultato.
Esercizi tipici e risultati attesi. Glucosio 0,30 M a 37 °C → ~7,63 atm (i = 1). NaCl 0,15 M a 37 °C con R in kPa → ~771,9 kPa (i = 2). Saccarosio 1,0 M a 0 °C → ~22,4 atm. HCl 1,0 M a 0 °C → ~44,8 atm (i ≈ 2). FeBr3 1,0 M a 0 °C → ~89,6 atm (i = 4). Se i cresce, cresce π.
Piccoli errori da evitare. Dimenticare il passaggio a Kelvin, scegliere un R incoerente con le unità, scordare i per gli elettroliti, trascurare α per elettroliti deboli quando richiesto, oppure usare concentrazioni troppo alte senza considerare deviazioni dall’idealità.
L’idea da portarsi a casa è che la pressione osmotica “misura” quante particelle agiscono nel volume di soluzione: numero di particelle (M), energia termica disponibile (T) e scala delle unità (R) determinano la forza necessaria per fermare il flusso osmotico. In ambito clinico e industriale, questo si traduce in scelte di concentrazione e di pressione applicata per mantenere l’equilibrio o separare solvente e soluto nel modo più efficiente possibile.