Como Converter Frações em Números Inteiros e Decimais: Guia Completo

Início » Ciência » Matemática » Como Converter Frações em Números Inteiros e Decimais: Guia Completo

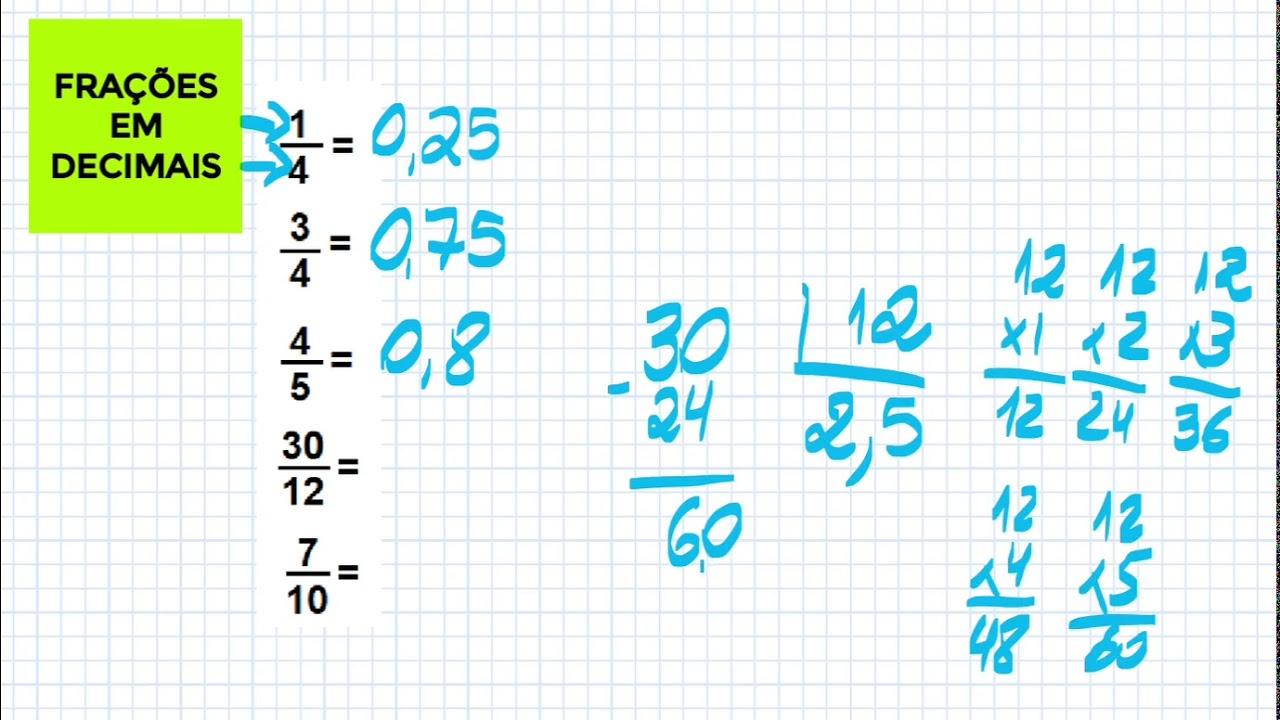
Quem lida com medidas, dinheiro, descontos ou receitas esbarra o tempo todo em frações e números decimais, e entender como transitar entre essas formas de escrever quantidades é essencial para evitar erros. Neste guia em português, você vai dominar converter frações em números inteiros e decimais, ler e comparar decimais e realizar operações com segurança no dia a dia.

Vamos percorrer um caminho que começa por um breve contexto histórico e vai até procedimentos práticos com exemplos detalhados, como 3/8, 10/16, 3,6 ÷ 0,4, além de multiplicação e divisão por potências de 10. De quebra, você verá dicas para quando a sua calculadora, planilha ou app interpreta 1/2 como 1, problema comum que pode ser resolvido com um simples ajuste no modo de divisão.

De onde vieram as frações e os decimais

As frações não surgiram por acaso: elas nasceram da necessidade de medir e repartir. Egípcios trabalhavam com frações do tipo 1/n (chamadas frações egípcias), como 1/2, 1/3 e 1/4, e até representavam frações mais complexas como soma dessas unitárias, por exemplo 5/6 = 1/2 + 1/3.

Outros povos adotaram convenções diferentes: os babilônios preferiam denominadores baseados no 60, e os romanos, no 12, escolhas ligadas ao grande número de divisores desses inteiros. A escrita das frações como usamos hoje consolidou-se por volta do século XVI, depois de um longo período de experimentos de notação.

Os números decimais, por sua vez, derivam de frações decimais, isto é, frações cujo denominador é uma potência de 10 (10, 100, 1000, …). 1/2 equivale a 5/10, que é o número decimal 0,5; converter frações decimais em decimais posicionais simplificou muito os cálculos práticos.

No fim do século XVI, Simon Stevin propôs um método sistemático para operar com decimais usando inteiros, marcando posições da vírgula; depois, John Napier ajudou a popularizar o uso do ponto ou vírgula para separar parte inteira e parte decimal. Os decimais ganharam terreno com a adoção do sistema métrico e a necessidade de precisão em áreas como astronomia.

Frações decimais e números decimais: o que são e como se relacionam

Frações com denominador 10, 100, 1000, 10^n são frações decimais, e toda fração decimal tem uma representação em notação decimal (com vírgula). 127/100 = 1,27; 8/10 = 0,8, onde 0 é a parte inteira e 8 a parte decimal.

A vírgula separa a parte inteira (PI) da parte decimal (PD), e essa escrita está baseada no valor posicional das casas. Decompor 127/100 como 100/100 + 27/100 mostra a passagem clara de fração para decimal.

Para ler um decimal, localize a vírgula e interprete as casas: décimos, centésimos, milésimos e assim por diante. Ex.: 0,189 = cento e oitenta e nove milésimos; 3,7 (três inteiros e sete décimos), 13,45 (treze inteiros e quarenta e cinco centésimos), 130,824 (cento e trinta inteiros e oitocentos e vinte e quatro milésimos).

Quando o denominador da fração já é uma potência de 10, a conversão é direta; se não for, você sempre pode efetuar a divisão do numerador pelo denominador. Dízimas exatas ou periódicas dependem dos fatores do denominador e são o próximo passo lógico dessa distinção.

Converter frações em números decimais (resultado exato quando possível)

Para transformar uma fração em decimal, basta dividir o numerador pelo denominador; é a leitura direta de a/b como a ÷ b. Se o denominador tem apenas fatores 2 e 5 (os primos do 10), o resultado é um decimal finito; do contrário, surge uma dízima periódica.

Exemplo clássico: 3/8. Podemos pensar em 3 como 3,0000… para facilitar a divisão por 8 sem mudar o valor do dividendo. Ao realizar 3 ÷ 8 = 0,375, obtemos o decimal exato.

Outro exemplo: 10/16. Como 10 é menor que 16, começamos com 0 vírgula e seguimos anexando zeros ao dividendo para continuar a divisão até zerar o resto. 10 ÷ 16 = 0,625, resultado exato porque 16 = 2^4.

Quando uma fração como 35/700 aparece, você pode simplificar antes (dividindo por 35) ou operar em formato decimal: 35 ÷ 700 = 0,05. Procedendo pela lógica da divisão, multiplica-se o dividendo por 100 para viabilizar a conta inteira 3500 ÷ 700 = 5 e, ao compensar o fator 100, volta-se a 0,05.

Converter números decimais em frações decimais

O caminho inverso também é direto: retire a vírgula, use como numerador o número sem vírgula e, como denominador, 1 seguido de tantos zeros quanto houver casas decimais. 2,41 = 241/100; quando possível, simplifique a fração dividindo numerador e denominador por um mesmo fator.

Esse procedimento formaliza a equivalência entre a forma decimal e a fração com potências de 10; ele é útil para operações ou demonstrações em que a escrita fracionária dá mais clareza. Alternar entre as formas pode reduzir passos de cálculo e tornar a justificativa mais transparente.

Zeros à direita da parte decimal: quando acrescentar não muda nada

Adicionar zeros após o último dígito não nulo da parte decimal não altera o valor do número. 0,5 = 0,50 = 0,500; esse truque é prático para alinhar casas decimais antes de somar ou subtrair.

Em contextos de medida, formatos com mais casas podem comunicar precisão ou convenção (como dinheiro com duas casas), mas matematicamente o número é o mesmo. Use as casas extras para facilitar operações em coluna sem medo de mudar o valor.

Multiplicar e dividir por potências de 10

Multiplicar um decimal por 10, 100, 1000, … desloca a vírgula para a direita 1, 2, 3, … casas. Desloca a vírgula para a direita; ex.: 7,4 × 10 = 74; 7,4 × 100 = 740.

Dividir por 10, 100, 1000, … desloca a vírgula para a esquerda 1, 2, 3, … casas. Dividir por 10 desloca a vírgula para a esquerda; ex.: 247,5 ÷ 10 = 24,75; 247,5 ÷ 100 = 2,475.

Adição e subtração com números decimais

Na soma e na subtração, o segredo é alinhar as casas decimais. Alinhe as casas decimais antes de operar e acrescente zeros à direita quando necessário.

Exemplos de preparação: 2,4 + 1,723 vira 2,400 + 1,723; do mesmo modo, 2,4 − 1,723 vira 2,400 − 1,723. Os zeros ajudam a evitar deslizes na posição das casas ao montar a conta em coluna.

Multiplicação de números decimais

Há dois jeitos equivalentes. Um é converter cada número para fração decimal, multiplicar numeradores e denominadores e, no fim, voltar à notação decimal. 2,25 × 3,5 = 7,875 (via frações).

O outro é multiplicar como se fossem inteiros e, ao final, posicionar a vírgula contando a soma das casas decimais do multiplicando e do multiplicador. Conte a soma das casas decimais para recolocar a vírgula no produto.

Divisão com números decimais

Para dividir, uma técnica poderosa é transformar a divisão em uma com inteiros, multiplicando dividendo e divisor por uma mesma potência de 10 para “cortar” a vírgula. Ex.: 3,6 ÷ 0,4 → 36 ÷ 4 = 9.

Se apenas o dividendo tem casas decimais (como 0,35 ÷ 7), multiplique ambos por 100 para obter 35 ÷ 700; simplificando ou dividindo, chegamos a 0,05. Multiplique tanto em cima quanto embaixo pelo mesmo fator para manter o quociente.

Quando o divisor é maior que o dividendo, a conta começa após a vírgula, com zeros sendo anexados ao dividendo até a divisão ficar possível. Acrescente zeros ao dividendo até que a divisão avance, ajustando a escala conforme necessário.

Em divisões como 10 ÷ 16, siga o algoritmo usual acrescentando zeros conforme necessário. O procedimento termina quando o resto zera ou ao reconhecer um período na dízima.

Como ler e comparar números decimais

Para comparar dois decimais, comece pela parte inteira: quem tem a parte inteira maior é o maior número. Compare primeiro a parte inteira antes de olhar as casas decimais.

Se as partes inteiras são iguais, iguale o número de casas decimais acrescentando zeros e compare as partes decimais como se fossem inteiros. Acrescente zeros para padronizar a comparação (ex.: 12,4 → 12,40 vs 12,31).

Essa técnica evita enganos visuais ao observar poucas casas em um número e muitas em outro. Padronizar as casas facilita a leitura direta sem erros.

Porcentagens como frações de 100

Porcentagem é uma forma padronizada de proporção em que comparamos valores usando o denominador 100. 30% = 30/100 e pode ser tratado como decimal conforme a necessidade.

Aplicações típicas são imediatas: uma sala com 30% de meninas indica que, em 100 alunos, 30 seriam meninas; se houver 200 estudantes, 30% correspondem a 60. 40% de 300,00 = 120,00 no comércio.

Outra situação: li 45% de um livro com 200 páginas; 45/100 = X/200 rende X = 90, então faltam 110 páginas. Converter percentuais para frações facilita encontrar o valor absoluto.

Quando uma fração vira número inteiro

Uma fração a/b representa um inteiro quando o numerador é múltiplo do denominador, isto é, quando a divisão a ÷ b não deixa resto. Ex.: 8/4 = 2, 15/5 = 3.

Nos demais casos, a fração vira um decimal finito (se o denominador, após simplificação, tem apenas 2 e 5 como fatores) ou uma dízima periódica. Simplifique a fração (veja frações equivalentes) e analise os fatores do denominador para decidir rapidamente.

Exemplos práticos detalhados

Exemplo 1: 3/8. Escreva 3 como 3,000… e divida por 8. 3 ÷ 8 = 0,375, sem resto.

Exemplo 2: 3,6 ÷ 0,4. Multiplique dividendo e divisor por 10 para obter 36 ÷ 4. Resultado: 9, estratégia simples e confiável.

Exemplo 3: 0,35 ÷ 7. Multiplique ambos por 100 e faça 35 ÷ 700. 35/700 simplifica para 5/100 = 0,05, mostrando o caminho fracionário e decimal.

Exemplo 4: 10/16. Divida 100 por 16 (após ajustar a escala) e prossiga anexando zeros ao resto quando necessário. Quociente: 0,625, resultado exato por causa da fatoração do denominador.

Dicas para operações com decimais no papel e no cotidiano

Antes de somar ou subtrair, alinhe as vírgulas e iguale as casas com zeros; na multiplicação, some as casas para posicionar a vírgula no produto; na divisão, transforme em divisão entre inteiros sempre que possível. Três âncoras: alinhar, somar casas e transformar divisões evitam a maioria dos erros.

Em compras e finanças, mantenha atenção às casas decimais do dinheiro; em unidades de medida, siga a convenção do contexto (duas ou três casas, por exemplo). Acrescentar zeros é útil para ganhar precisão nas contas até encontrar resto zero ou padrão periódico.

Leitura e escrita: vírgula, parte inteira e parte decimal

É comum confundir ponto e vírgula em contextos internacionais; em português, a vírgula separa a parte inteira da decimal. 4,37 = quatro inteiros e trinta e sete centésimos, e 0,8 indica oito décimos.

Ao decompor um decimal, enxergue-o como soma da parte inteira e da fração decimal correspondente. 1,27 = 1 + 27/100, leitura útil em justificativas passo a passo.

Quando a sua ferramenta lê 1/2 como 1: como contornar

Às vezes, ao digitar 1/2 em uma fórmula de planilha ou app, o sistema interpreta como texto ou aplica divisão inteira, devolvendo 1. Realize a divisão com casas decimais (ou escreva 1 ÷ 2) para evitar truncamento.

Se o campo aceitar apenas números, converta 1/2 para 0,5 antes, ou reescreva como 1 ÷ 2; se o sistema fizer corte inteiro, ajuste a configuração para divisão real (decimal). 1/2 representa 0,5 quando a operação é feita corretamente.

Vale gravar que a/b vira um inteiro quando a divisão é exata, um decimal finito quando o denominador simplificado tem apenas 2 e 5 como fatores, e uma dízima nos demais casos; acrescentar zeros ou deslocar a vírgula são ferramentas de precisão, não truques: são a própria lógica do sistema decimal operando a seu favor.