A dilatação superficial é um fenômeno físico que ocorre quando um material sofre alterações em sua área devido a variações de temperatura. Para calcular a variação da área de um corpo submetido a esse processo, utilizamos a fórmula:
ΔA = A . α . ΔT
Onde ΔA representa a variação da área, A a área inicial, α o coeficiente de dilatação superficial e ΔT a variação de temperatura. Os coeficientes de dilatação superficial variam de acordo com o material e podem ser positivos ou negativos.
Alguns exemplos de dilatação superficial são a expansão de uma lâmina metálica em contato com o calor, a deformação de uma placa de vidro exposta ao sol e a dilatação da superfície de um líquido contido em um recipiente aquecido. A compreensão desse fenômeno é essencial para diversos campos da engenharia e da física, contribuindo para o desenvolvimento de tecnologias e materiais mais eficientes e duráveis.
Conceito e cálculo da dilatação superficial em materiais: entenda suas fórmulas e aplicações práticas.
A dilatação superficial é um fenômeno físico que ocorre quando um material sofre alterações em suas dimensões superficiais devido à variação de temperatura. Para calcular a dilatação superficial de um material, utilizamos fórmulas específicas que levam em consideração o coeficiente de dilatação superficial do material em questão.
A fórmula geral para calcular a dilatação superficial é:
ΔA = A0 * α * ΔT
Onde:
ΔA é a variação da área superficial;
A0 é a área inicial do material;
α é o coeficiente de dilatação superficial do material; e
ΔT é a variação de temperatura.
Para calcular a dilatação superficial, é importante conhecer o coeficiente de dilatação superficial do material em questão, que pode variar de acordo com o tipo de material. Com base nesse coeficiente, é possível prever como a área superficial do material irá se alterar conforme a temperatura varia.
Um exemplo prático de dilatação superficial pode ser observado em placas metálicas expostas ao sol. Conforme a temperatura aumenta, as placas metálicas se expandem, alterando suas dimensões superficiais. Essa variação de área pode ser calculada utilizando a fórmula mencionada anteriormente.
Portanto, compreender o conceito e o cálculo da dilatação superficial em materiais é essencial para diversos campos da engenharia e da física, permitindo prever e controlar as alterações dimensionais dos materiais em diferentes condições de temperatura.
Descubra o coeficiente de dilatação superficial e sua importância em materiais.
A dilatação superficial é um fenômeno físico que ocorre quando um material sofre um aumento de área devido ao aumento de temperatura. Para calcular esse efeito, utilizamos o coeficiente de dilatação superficial, que é uma grandeza física que representa a variação da área de um material em relação à variação de temperatura.
O coeficiente de dilatação superficial é representado pela letra grega alpha (α) e possui unidades de 1/°C. Ele é calculado pela fórmula:
α = (ΔA / A0) / ΔT
Onde ΔA é a variação da área, A0 é a área inicial e ΔT é a variação de temperatura.
É importante conhecer o coeficiente de dilatação superficial de um material, pois ele permite prever o comportamento desse material em diferentes situações de temperatura. Materiais com coeficientes de dilatação superficiais altos tendem a se expandir mais facilmente com o aumento de temperatura, enquanto materiais com coeficientes baixos terão uma dilatação mais limitada.
Por exemplo, o vidro possui um coeficiente de dilatação superficial menor que o aço. Isso significa que, quando expostos a altas temperaturas, o vidro irá se expandir menos que o aço, o que pode ser crucial em aplicações onde a precisão dimensional é importante, como na fabricação de componentes eletrônicos.
Em resumo, o coeficiente de dilatação superficial é uma ferramenta importante para entender e prever o comportamento dos materiais em diferentes condições de temperatura, sendo fundamental para diversas áreas da engenharia e da ciência dos materiais.
Descubra os coeficientes de dilatação dos materiais mais comuns utilizados na indústria.
Dilatação superficial é um fenômeno físico que ocorre quando um material sofre uma mudança em sua área devido ao aumento da temperatura. Para calcular a dilatação superficial de um material, utilizamos a fórmula:
ΔA = A * α * ΔT
Onde ΔA é a variação da área, A é a área inicial do material, α é o coeficiente de dilatação superficial e ΔT é a variação de temperatura.
Os coeficientes de dilatação superficial dos materiais mais comuns utilizados na indústria são:
– Ferro: 6,5 x 10^-6 °C^-1
– Alumínio: 23 x 10^-6 °C^-1
– Vidro: 8 x 10^-6 °C^-1
– Cobre: 19 x 10^-6 °C^-1
Esses valores representam a variação da área de cada material para cada grau de aumento de temperatura. Quanto maior o coeficiente de dilatação superficial, maior será a variação da área do material com o aumento da temperatura.
Um exemplo prático de dilatação superficial é quando uma placa de metal é aquecida e sofre uma expansão em sua área. Isso ocorre devido ao aumento da agitação das partículas do material com o aumento da temperatura, fazendo com que ele se expanda.
Portanto, compreender os coeficientes de dilatação superficial dos materiais é essencial para prever como eles irão se comportar em diferentes condições de temperatura, sendo fundamental para a indústria e para o desenvolvimento de diversos produtos.
Descubra a fórmula para calcular o coeficiente de dilatação de materiais.
Quando um material é aquecido, ele se expande e quando é resfriado, ele se contrai. Esse fenômeno é conhecido como dilatação térmica. Quando essa dilatação ocorre apenas na superfície do material, chamamos de dilatação superficial.
O coeficiente de dilatação superficial, representado pela letra gama (γ), é uma grandeza que indica o quanto a área de um material se expande a cada variação de temperatura. A fórmula para calcular o coeficiente de dilatação superficial é:
γ = ΔA / (A0 * ΔT)
Onde:
– γ é o coeficiente de dilatação superficial
– ΔA é a variação de área
– A0 é a área inicial
– ΔT é a variação de temperatura
Para encontrar o valor do coeficiente de dilatação superficial de um material, basta medir a variação de área, a área inicial e a variação de temperatura e aplicar na fórmula acima.
Alguns exemplos de coeficientes de dilatação superficial são:
– Água: 0,00021 ºC^-1
– Ferro: 0,000012 ºC^-1
– Alumínio: 0,000023 ºC^-1
A dilatação superficial é um fenômeno comum em nosso dia a dia e compreender o coeficiente de dilatação dos materiais ajuda a prever e controlar as variações de temperatura em diferentes situações.
Dilatação superficial: fórmula, coeficientes e exemplos
A expansão da superfície , é a expansão que ocorre quando um objecto submetido a variações na sua superfície por causa de uma variação de temperatura. Isso se deve às características do material ou à sua forma geométrica. A dilatação predomina em duas dimensões na mesma proporção.
Por exemplo, em uma folha, quando há uma variação de temperatura, é a superfície da folha que sofre a maior alteração devido à expansão térmica.

A chapa metálica da figura anterior aumenta sua largura e comprimento consideravelmente quando é aquecida por radiação solar. Pelo contrário, ambos diminuem significativamente quando são resfriados devido a uma diminuição da temperatura ambiente.
É por esse motivo que, quando os ladrilhos são instalados no piso, algumas arestas não devem ser coladas umas às outras, mas deve haver um espaço chamado junta de expansão.
Além disso, esse espaço é preenchido com uma mistura especial que possui um certo grau de flexibilidade, impedindo que os ladrilhos se quebrem devido às fortes pressões que a expansão térmica pode produzir.
O que é dilatação superficial?
Em um material sólido, os átomos mantêm suas posições relativas mais ou menos fixadas em torno de um ponto de equilíbrio. No entanto, devido à agitação térmica, eles estão sempre girando em torno dele.
À medida que a temperatura aumenta, a oscilação térmica também aumenta, fazendo com que as posições médias de oscilação mudem. Isso ocorre porque o potencial de ligação não é exatamente parabólico e tem assimetria em torno do mínimo.
Abaixo está uma figura que descreve a energia da ligação química em função da distância interatômica. Também mostra a energia total de oscilação em duas temperaturas e como o centro da oscilação se move.

Dilatação superficial e seu coeficiente
Para medir a expansão superficial, partimos de uma área inicial A e de uma temperatura inicial T, cujo objeto queremos medir a expansão.
Suponha que o referido objeto seja uma folha da área A e sua espessura seja muito menor que a raiz quadrada da área A. S e submeta a folha a uma variação de temperatura ΔT, de modo que a temperatura final do Uma vez estabelecido o equilíbrio térmico com a fonte de calor, será T ‘= T + ΔT.
Durante esse processo térmico, a área da superfície também mudou para um novo valor A ‘= A + ΔA, onde ΔA é a variação no comprimento. Assim, s e define o coeficiente de expansão da superfície σ como o quociente entre a variação relativa da área por unidade de variação de temperatura.
A fórmula a seguir define o coeficiente de expansão da superfície σ:
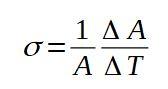
O coeficiente de expansão da superfície σ é praticamente constante para uma ampla faixa de valores de temperatura.
Pela definição de σ, suas dimensões são inversas à temperatura. Como uma unidade, geralmente é usado ° C -1 .
Coeficiente de expansão da superfície para vários materiais
Abaixo, listaremos o coeficiente de expansão da superfície de alguns materiais e elementos. O coeficiente é calculado à pressão atmosférica normal, com base em uma temperatura ambiente de 25 ° C, e seu valor é considerado constante em uma faixa de ΔT de -10 ° C a 100 ° C.
A unidade do coeficiente de expansão da superfície será (° C) -1
– Aço: σ = 24 ∙ 10 -6 (° C) -1
– Alumínio: σ = 46 ∙ 10 -6 (° C) -1
– Ouro: σ = 28 ∙ 10 -6 (° C) -1
– Cobre: σ = 34 ∙ 10 -6 (° C) -1
– Latão: σ = 36 ∙ 10 -6 (° C) -1
– Ferro: σ = 24 ∙ 10 -6 (° C) -1
– Vidro: σ = (14 a 18) ∙ 10 -6 (° C) -1
– Quartzo: σ = 0,8 ∙ 10 -6 (° C) -1
– Diamante: σ = 2 ,, 4 ∙ 10 -6 (° C) -1
– Chumbo: σ = 60 ∙ 10 -6 (° C) -1
– Madeira de carvalho: σ = 108 ∙ 10 -6 (° C) -1
– PVC: σ = 104 ∙ 10 -6 (° C) -1
– Fibra de carbono: σ = -1,6 ∙ 10 -6 (° C) -1
– Concreto: σ = (16 a 24) ∙ 10 -6 (° C) -1
A maioria dos materiais estica com um aumento de temperatura. No entanto, alguns materiais como fibra de carbono encolhem com o aumento da temperatura.
Exemplos resolvidos de expansão superficial
Exemplo 1
Uma chapa de aço tem dimensões de 3m x 5m. De manhã e à sombra, a temperatura é de 14 ° C, mas ao meio-dia o sol a aquece a 52 ° C. Encontre a área final da placa.
Solução
Começamos com a definição de coeficiente de expansão da superfície:
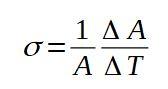
A partir daqui, limpamos a variação na área:

Em seguida, procedemos a substituir os respectivos valores para encontrar o aumento da área pelo aumento da temperatura.

Ou seja, a área final será de 15.014 metros quadrados.
Exemplo 2
Mostre que o coeficiente de expansão da superfície é aproximadamente o dobro do coeficiente de expansão linear.
Solução
Suponha que partimos de uma placa retangular de dimensões largura Lx e comprimento Ly, então sua área inicial será A = Lx ∙ Ly
Quando a placa sofre um aumento de temperatura ΔT, suas dimensões também aumentam, sendo sua nova largura Lx ‘e seu novo comprimento Ly’, de modo que sua nova área será A ‘= Lx’ ∙ Ly ‘

A variação sofrida pela área da placa devido à mudança de temperatura será então
ΔA = Lx ‘∙ Ly’ – Lx ∙ Ly
em que Lx ‘= Lx (1 + α AT) e Ly’ = Ly (1 + α AT)
Ou seja, a mudança de área em função do coeficiente de expansão linear e a mudança de temperatura serão:
ΔA = Lx (1 + αΔT) ∙ Ly (1 + α ΔT) – Lx ∙ Ly
Isso pode ser reescrito como:
ΔA = Lx ∙ Ly ∙ (1 + α ΔT) ² – Lx ∙ Ly
Desenvolvendo o quadrado e multiplicando, temos o seguinte:
ΔA = Lx ∙ Ly + 2α ΔT Lx ∙ Ly + (α ΔT) ² Lx ∙ Ly – Lx ∙ Ly
Como α é da ordem de 10 -6 , quando elevado ao quadrado, é da ordem de 10 -12 . Assim, o termo quadrático na expressão anterior é desprezível.
Em seguida, o aumento da área pode ser aproximado por:
ΔA ≈ 2α ΔT Lx ∙ Ly
Mas o aumento da área, dependendo do coeficiente de expansão da superfície, é:
ΔA = ΔT A
Da qual é deduzida uma expressão que relaciona o coeficiente de expansão linear ao coeficiente de expansão da superfície.
γ ≈ 2 ∙ α
Referências
- Bauer, W. 2011. Física para Engenharia e Ciência. Volume 1. Mac Graw Hill. 422-527
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6o. Edição Prentice Hall. 238-249.