Entropia (Termodinamica): significato, formule e applicazioni

Início » Ciência » Física » Entropia (Termodinamica): significato, formule e applicazioni

L’entropia è una di quelle idee che, una volta capita, cambia il modo in cui guardiamo fenomeni quotidiani e leggi fondamentali della natura: dal profumo che si diffonde nella stanza alla miscela irreversibile di due gas, fino ai limiti ultimi delle macchine termiche e all’andamento del tempo fisico. In termodinamica, l’entropia misura la tendenza dei sistemi a evolvere verso configurazioni più probabili, cioè più «disordinate» nel senso statistico del termine.

Non si tratta solo di una grandezza utile per calcolare il rendimento di una macchina: il concetto si estende alla meccanica statistica, alla meccanica quantistica e persino alla teoria dell’informazione e all’economia. Il termine, coniato da Rudolf Clausius nel 1864, nasce sul solco tracciato da Sadi Carnot (1824) e affonda le radici nel greco antico: en (dentro) e tropé (trasformazione), cioè «trasformazione interna». Clausius formalizzò l’idea che una parte dell’energia fornita a un sistema diventa irrimediabilmente indisponibile a compiere lavoro, introducendo così la funzione di stato entropia.

Origine storica, idee intuitive e primi esempi

Clausius definì l’entropia come il rapporto tra il calore scambiato reversibilmente e la temperatura assoluta, una scelta che cattura l’irreversibilità osservata nei processi reali. L’onda lunga del concetto ha attraversato l’Ottocento e il Novecento, uscendo dai confini della fisica per ispirare informatica, teoria dei segnali, scienze sociali ed economia.

Un buon modo per entrare nel tema è partire dagli esempi. Se una goccia d’inchiostro cade in un bicchiere d’acqua, si diffonde fino a uniformarsi; il processo inverso, ristabilire la goccia separata, non avviene spontaneamente e richiede lavoro esterno. Lo stesso accade quando si stappa un profumo: le molecole evaporano e si disperdono, finché l’aria circostante si arricchisce del loro odore; non c’è un ritorno spontaneo allo stato iniziale perfettamente ordinato.

• Mescolamento di gas: due gas inizialmente separati, messi in comunicazione, si mescolano fino a formare una miscela uniforme; l’entropia aumenta (la cosiddetta variazione di entropia di miscelamento).
• Materiali metallici: una struttura cristallina ha ordine a lungo raggio, una policristallina ha ordine a corto raggio, un solido amorfo è disordinato; difetti cristallini (vacanze, sostituzioni) aumentano l’entropia.

Queste intuizioni si riassumono bene nell’idea popolare di entropia come «grado di disordine». Attenzione però: «disordine» è una scorciatoia linguistica, utile ma non rigorosa; il nocciolo è la probabilità dei microstati. In natura, i macrostati che possono essere realizzati da più configurazioni microscopiche sono i più probabili, perciò i sistemi “vanno” in quella direzione.

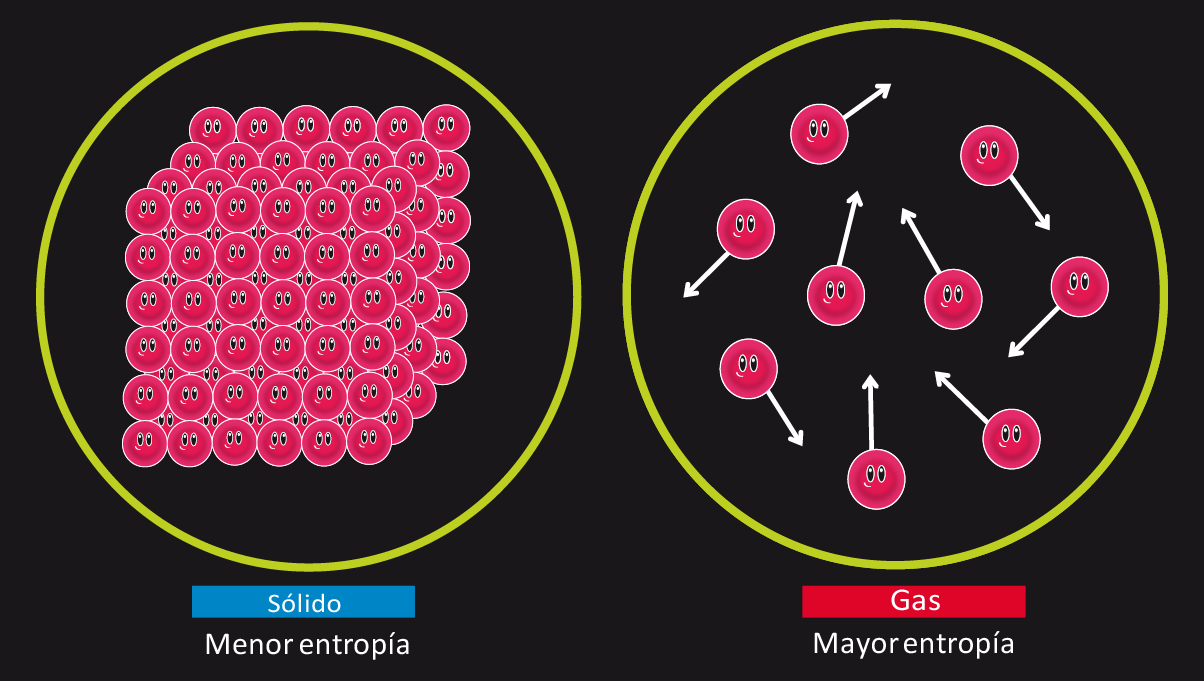
Definizioni termodinamiche e secondo principio

In termodinamica classica distinguiamo sistema e ambiente: il sistema è la porzione di universo che studiamo, delimitata da pareti o confini che possono scambiare o meno materia e calore; tutto il resto è l’ambiente. Le variabili di stato principali sono temperatura T, pressione P, volume V. Il primo principio (conservazione dell’energia) introduce l’energia interna U, ma non dice nulla sulla direzione dei processi.

Qui entra in gioco il secondo principio, che possiamo enunciare in vari modi equivalenti. Formulazione di Kelvin–Planck: non è possibile realizzare una trasformazione il cui unico risultato sia la conversione completa in lavoro del calore proveniente da un’unica sorgente a temperatura uniforme. In altre parole, non esistono macchine termiche perfette. La formulazione di Clausius è speculare: il calore non fluisce spontaneamente da freddo a caldo.

Clausius introdusse anche la disuguaglianza integrale: su un ciclo qualunque, ∮ δQ/T ≤ 0. Spezzando il ciclo in andata irreversibile e ritorno reversibile e usando il fatto che dS = δQ_rev/T, si ottiene che, per un sistema isolato, l’entropia non diminuisce (S2 ≥ S1). Questa è la fisionomia matematica dell’irreversibilità, il motivo per cui il «tempo termodinamico» ha un verso.

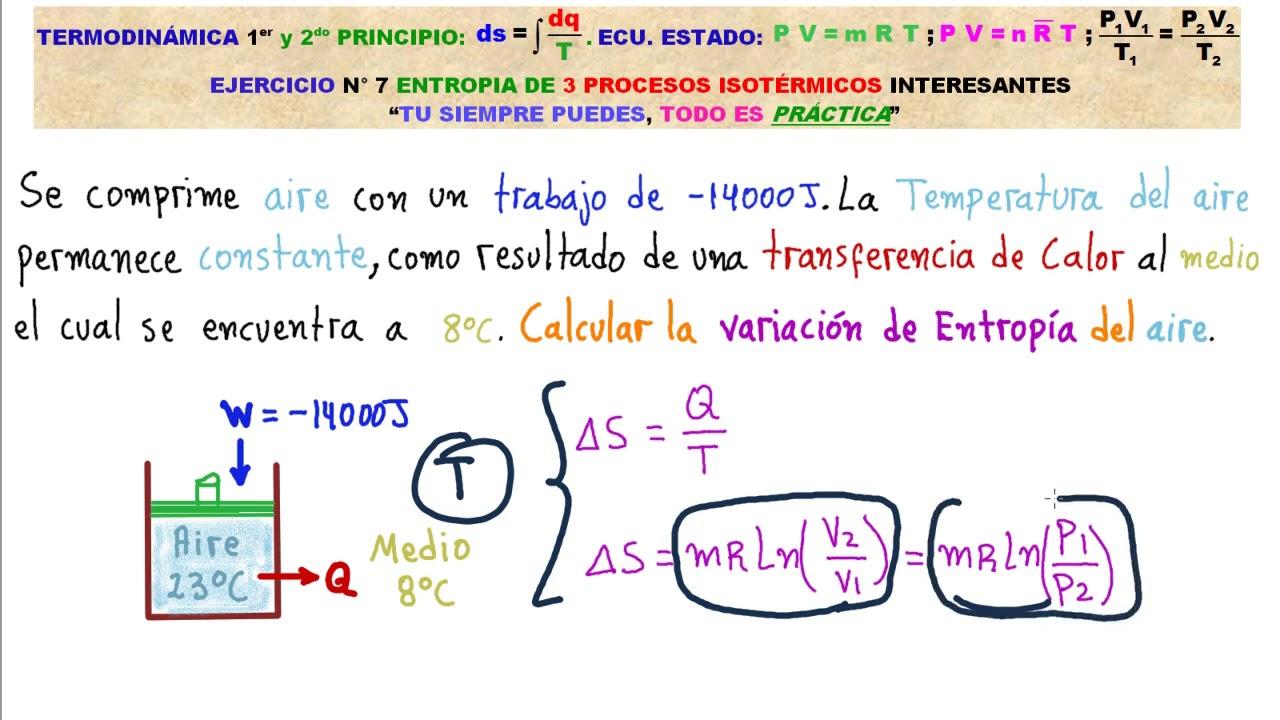
Sui sistemi isolati valgono due frasi potenti: l’energia totale resta costante e l’entropia totale cresce, fino a raggiungere l’equilibrio. Applicando l’idea all’intero universo come grande sistema isolato, il quadro porta alla celebre «morte termica», uno stato di temperatura uniforme e assenza di energia libera capace di compiere lavoro.

Un dettaglio spesso trascurato ma cruciale: l’entropia è una funzione di stato. Ciò significa che la sua variazione tra A e B non dipende dal percorso, per cui possiamo calcolarla seguendo qualsiasi cammino reversibile tra gli stessi stati. Questa proprietà sblocca i calcoli pratici e collega strettamente l’entropia al secondo principio.

Formule utili per gas ideali e cambi di fase

Quando gli scambi di calore avvengono in modo reversibile, dS = δQ_rev/T. Per processi elementari possiamo integrare lungo un cammino reversibile opportuno. Nei gas ideali, isotermi (T costante) forniscono risultati compatti: usando PV = nRT, si ottiene per n moli ΔS|_T = nR ln(VB/VA) e, in forma equivalente, ΔS|_T = nR ln(pA/pB) se non c’è lavoro isocoro.

Per riscaldamenti a volume costante, con calore specifico molare cv funzione di T, si ha ΔS = ∫(n·cv dT/T) = n·c̄v ln(TB/TA); in modo analogo a pressione costante con cp: ΔS = n·c̄p ln(TB/TA). Combinando un’isocora reversibile e un’isoterma reversibile tra A e B si ottiene una forma generale per i gas ideali: ΔS = n·cV ln(TB/TA) + n·R ln(VB/VA).

Integrando e scegliendo una costante additiva, si trova un’espressione analitica della funzione stessa (per i gas ideali): S = n·cV ln T + n·R ln V + costante, equivalente a scritture alternative come S = n·cV ln(T·V^{γ−1}) = n·cV ln(p·V^{γ}) (con γ = cp/cv). Nelle adiabatiche reversibili (δQ = 0) l’entropia resta costante, motivo per cui si parla di trasformazioni isoentropiche.

Nei solidi e nei liquidi bisogna contare anche i contributi dei salti di fase. Per una sostanza che attraversa fusione ed ebollizione, l’entropia molare si ricava sommando gli integrali dei cp/T nelle diverse fasi e i termini ΔH_fus/T_fus e ΔH_eb/T_eb. Questo schema è la ricetta standard per calcolare entropie assolute partendo da 0 K (vedi più avanti il terzo principio). Per fenomeni come la transizione diretta da solido a gas, vedi anche sublimazione.

Visione statistica e quantistica: da Boltzmann a von Neumann

La meccanica statistica fornisce il significato microscopico dell’entropia. Boltzmann legò l’entropia al numero Γ di microstati compatibili con un macrostato: S = k ln Γ (k è la costante di Boltzmann). Se un macrostato può essere realizzato in molti modi a livello molecolare, è più probabile e ha entropia più alta. Ecco perché «disordine» è sinonimo pratico di «maggiore numerosità di microstati».

Un esempio illuminante è la miscelazione in un cristallo: avendo NA atomi A e NB atomi B da distribuire su N siti, il numero di configurazioni massime è Γ = (NA + NB)! / (NA!·NB!). Se le specie aumentano (A, B, C, …), Γ = (∑i Ni)! / ∏i Ni!. Più disposizioni possibili significa entropia maggiore. A temperatura ordinaria i gas seguono la distribuzione di Maxwell–Boltzmann; a basse temperature entrano in gioco Fermi–Dirac e Bose–Einstein, perché le particelle riempiono i livelli più bassi secondo regole quantistiche e (per i fermioni) il principio di esclusione.

Un altro tassello fondamentale è la formula di Gibbs per sistemi con microstati discreti: S = −k ∑i pi ln pi, che coincide con l’entropia di Shannon in informazione. Si dimostra la piena equivalenza con la definizione classica differenziale dS = δQ/T lungo i processi reversibili, saldando termodinamica e statistica.

Nel quadro quantistico entra l’entropia di von Neumann: S = −k Tr(ρ ln ρ), con ρ matrice densità. Se consideriamo due sottosistemi A e B in uno stato entangled puro del tipo «a due stati», la traccia parziale sul sottosistema opposto fornisce uno stato misto per A con entropia k ln 2 (il massimo per un sistema binario), mentre il sistema complessivo, essendo puro, ha S = 0. Gli operatori unitari non cambiano l’entropia, legando reversibilità dinamica e costanza dell’entropia nel dominio quantistico.

Sistemi aperti, chiusi, isolati: bilanci di entropia

Nel mondo reale i sistemi scambiano massa ed energia con l’esterno. Per un volume di controllo conviene scrivere un bilancio di entropia: Ṡ = JS + ∂S/∂t, dove JS è la corrente netta di entropia attraverso i confini e ∂S/∂t è la produzione interna, che per il secondo principio è non negativa.

Esplicitando i contributi si ottiene Ṡ = ∑i (Q̇i/Ti + ṁi si) + ∂S/∂t: il termine conduttivo Q̇i/Ti rappresenta scambi di calore con sorgenti a temperatura Ti, il termine convettivo ṁi si l’entropia che entra/esce con la massa (si è l’entropia specifica). In un sistema chiuso i termini convettivi si annullano; in un sistema isolato si annullano anche i flussi di calore, per cui Ṡ = ∂S/∂t ≥ 0.

Nel mondo biologico la situazione è esplicita: gli organismi, essendo sistemi aperti, mantengono ordine interno scambiando materia ed energia e esportando entropia verso l’esterno.

Materiali, ordine e difetti: entropia nelle strutture solide

Nei materiali metallici l’entropia è un marcatore di ordine strutturale. Nelle strutture cristalline perfette, gli atomi occupano posizioni regolari (ordine a lungo raggio) e l’entropia è relativamente bassa. In materiali policristallini c’è ordine a corto raggio fra domini; nei vetri amorfi domina il disordine. Difetti cristallini, vacanze, interstiziali o sostituzionali aumentano le configurazioni disponibili e quindi alzano l’entropia del materiale.

Informazione ed economia: dal teorema di Shannon a Georgescu-Roegen

Claude Shannon, nel 1948, ha mostrato che l’entropia di una sorgente casuale è il limite inferiore della compressione: non si può codificare un messaggio con un numero medio di bit inferiore alla sua entropia (prima codifica di sorgente). L’entropia quantifica l’incertezza media e si intreccia con la teoria dei segnali: ridondanza, rumore e capacità di compressione hanno un legame profondo con le distribuzioni di probabilità.

In economia, Nicholas Georgescu‑Roegen ha esteso il secondo principio ai processi produttivi: ogni produzione aumenta l’entropia del sistema Terra, rendendo parte dell’energia non più disponibile e proiettando nel futuro i vincoli fisici dello sviluppo. Nel mercato finanziario, l’informazione tende a diffondersi probabilisticamente: una nuova informazione raramente resta isolata, perché gli agenti hanno incentivo a sfruttarla, incorporandola nei prezzi. Più alto è l’«entropia informativa» del mercato, più rapido è l’assorbimento dell’informazione e maggiore l’imprevedibilità (rumore), tratti coerenti con l’ipotesi di efficienza informativa.

Terzo principio e entropie standard: riferimenti assoluti

Il teorema di Nernst (terzo principio) stabilisce che l’entropia di un cristallo perfetto tende a zero quando T → 0 K. Questo fornisce lo zero naturale della scala, consentendo di tabulare entropie assolute standard S° a 1 atm e 25 °C.

Regole d’uso rapide: a parità di sostanza, Svapore > Sliquido > Ssolido; a parità di fase, molecole più complesse hanno S più alta; fra forme allotropiche, la più ordinata ha S minore; per specie monoatomiche, più è pesante l’atomo, maggiore tende a essere S (più livelli energetici accessibili). Queste tendenze aiutano a stimare il segno di ΔS nelle reazioni e nei cambi di fase.

La spontaneità, in ambiente a T e P costanti, dipende dalla competizione tra entalpia (ΔH) ed entropia (ΔS) tramite l’energia libera: processi con dispersione di energia (ΔH < 0) e aumento di disordine (ΔS > 0) sono fortemente favoriti. Quando ΔS < 0, occorre un ΔH sufficientemente negativo per guidare il processo, e viceversa. Per la dinamica delle reazioni e il concetto di energia libera vedi anche reazioni endergoniche.

Ordine, probabilità e ritorni «impossibili»

La chiave concettuale è probabilistica: gli eventi evolvono verso ciò che è immensamente più probabile. Il calore passa da caldo a freddo perché l’inverso richiederebbe fluttuazioni coordinate milionesime oltre ogni scala osservabile. Formalmente, l’equazione di Boltzmann S = k ln W dice che un aumento di entropia corrisponde a W finale maggiore di W iniziale: più microstati accessibili ci sono, più grande è S.

Questo chiarisce perché i processi reali siano irreversibili: una volta convertito lavoro in calore, riottenere integralmente lavoro richiederebbe un percorso microscopico straordinariamente specifico, statisticamente trascurabile. Nei cicli termodinamici ideali si può riportare il sistema allo stato iniziale, ma solo a costo di aumentare l’entropia altrove (nell’ambiente o nell’agente che esegue il ciclo).

Un’analogia intuitiva: una pallina su un pendio scende spontaneamente verso valle; portarla in cima è possibile, ma serve lavoro. Allo stesso modo si può ridurre localmente l’entropia (costruire ordine), ma il prezzo è un aumento maggiore altrove. Questa è la logica che regge anche i sistemi viventi.

Sistemi viventi e strutture dissipative

Da Schrödinger a Prigogine, da Boltzmann a Brillouin e alla nozione di neghentropia, molti hanno indagato come gli organismi, apparentemente «contro» l’aumento di entropia, mantengano ordine interno. La risposta è che vivono scambiando energia e materia con l’ambiente, esportando entropia verso l’esterno; in termini termodinamici fanno parte di sistemi aperti che possono ridurre localmente S a spese di un incremento globale.

Le strutture dissipative studiate da Prigogine nascono lontano dall’equilibrio: ordine dinamico mantenuto grazie a flussi continui. Non c’è violazione del secondo principio, ma piuttosto la sua realizzazione in sistemi non lineari dove la produzione di entropia è il «costo» per sostenere forme organizzate.

Casi didattici e osservazioni operative

Tre classici esperimenti mentali illustrano bene la direzionalità dei processi: contatto tra corpi a diversa temperatura (calore da caldo a freddo), miscelazione di gas diversi (crescita di S), impatto di una pietra a terra (energia meccanica dispersa come calore). Il primo principio è rispettato in entrambe le direzioni, ma il secondo seleziona il verso che osserviamo nella realtà.

In pratica, per stimare ΔS di reazione in condizioni standard si usa ΔS° = Σν S°(prodotti) − Σν S°(reagenti) (con i coefficienti stechiometrici). Per le macchine termiche reali, la differenza fra scambi termici a diverse temperature è ciò che impone un rendimento sempre inferiore a 1, coerentemente con la formulazione Kelvin–Planck.

Infine, la relazione con l’informazione aiuta a costruire un ponte concettuale: ridurre l’incertezza costa risorse, così come comprimere dati fino al limite Shannon richiede codifiche ideali; nella fisica, ridurre entropia in un sottosistema richiede lavoro ed è pagato con un aumento altrove. Le due facce, termica e informativa, si rispecchiano nelle formule di Gibbs/Shannon e von Neumann.

Quanto discusso evidenzia un filo continuo: dall’intuizione storica di Clausius e Carnot alle formule operative per gas, fasi e reazioni; dalla lettura statistico‑quantistica alla dinamica dei sistemi aperti; dai limiti delle macchine al modo in cui informazione e mercati si diffondono e si «equilibrano». L’entropia è la bussola che orienta la direzione dei processi naturali e, allo stesso tempo, lo strumento che li rende calcolabili con precisione.