O momento de torção é um conceito fundamental na área da mecânica dos materiais, sendo responsável por transmitir forças de torção em uma determinada estrutura. Neste artigo, iremos abordar as características do momento de torção, as fórmulas utilizadas para seu cálculo e também propor alguns exercícios práticos para auxiliar na compreensão e aplicação desse conceito. O momento de torção é essencial para o dimensionamento de peças e estruturas sujeitas a esforços de torção, sendo de extrema importância para garantir a segurança e eficiência dos projetos de engenharia.
Entendendo o conceito de momento de torção em materiais estruturais e engenharia mecânica.
Entendendo o conceito de momento de torção em materiais estruturais e engenharia mecânica é fundamental para o projeto e análise de diversos tipos de estruturas. O momento de torção, também conhecido como torque, é uma força que tende a torcer um objeto em torno de seu eixo longitudinal.
Em materiais estruturais, o momento de torção é uma das principais cargas que podem atuar sobre um elemento, podendo causar deformações e falhas se não for adequadamente considerado no projeto. Na engenharia mecânica, o momento de torção é essencial para o dimensionamento de eixos, veios e outras peças sujeitas a esse tipo de carga.
Para calcular o momento de torção em um material estrutural, utiliza-se a fórmula: T = F * d, onde T é o momento de torção, F é a força aplicada e d é a distância entre o ponto de aplicação da força e o eixo de rotação. Outra fórmula importante relacionada ao momento de torção é a fórmula de resistência do material, que considera a tensão de cisalhamento e a área da seção transversal do elemento.
Para exemplificar o cálculo do momento de torção, vamos considerar um eixo de aço submetido a uma força de 500 N a uma distância de 0,3 m do eixo de rotação. Nesse caso, o momento de torção seria de 150 Nm (newton-metro). É importante ressaltar que o momento de torção deve ser calculado com precisão para garantir a segurança e a eficiência das estruturas.
Em resumo, o momento de torção é uma carga essencial em materiais estruturais e engenharia mecânica, sendo fundamental para o dimensionamento e análise de diversas estruturas. Compreender o conceito e as fórmulas relacionadas ao momento de torção é essencial para o desenvolvimento de projetos seguros e eficientes.
Fórmula do torque: como calcular e aplicar esse conceito fundamental da física mecânica.
O torque é uma grandeza física fundamental na mecânica, que está relacionada à rotação de um objeto em torno de um eixo. Ele é responsável por produzir uma rotação em um objeto quando uma força é aplicada a uma certa distância desse eixo. Para calcular o torque, utilizamos a fórmula:
Torque (τ) = Força (F) x Braço de alavanca (r)
Onde a força é a magnitude da força aplicada e o braço de alavanca é a distância entre o ponto de aplicação da força e o eixo de rotação. O torque é medido em Newton metro (Nm) no Sistema Internacional de Unidades.
Para aplicar esse conceito, é importante considerar a direção da força em relação ao eixo de rotação. Se a força e o braço de alavanca estiverem na mesma direção, o torque será máximo. Caso contrário, será necessário calcular o componente da força perpendicular ao braço de alavanca.
Além disso, é importante ressaltar que o torque é uma grandeza vetorial, ou seja, possui direção e sentido. A direção do torque é determinada pela regra da mão direita, onde o polegar aponta para o eixo de rotação e os dedos indicam a direção da força.
Para realizar cálculos envolvendo torque, é possível resolver diversos exercícios práticos que envolvem situações do cotidiano. Esses exercícios ajudam a compreender melhor como o torque atua em diferentes situações e como é possível determinar sua magnitude e direção.
Em resumo, o torque é uma grandeza fundamental na física mecânica, que está diretamente relacionada à rotação de objetos em torno de um eixo. Utilizando a fórmula correta e compreendendo seu significado, é possível calcular e aplicar o torque em diversas situações do dia a dia.
Fórmula para calcular o momento resultante em um sistema de forças.
O momento resultante em um sistema de forças pode ser calculado utilizando a fórmula:
Momento Resultante = Σ(Mi)
Onde Σ(Mi) representa a soma dos momentos individuais de cada força que atua no sistema. Para calcular o momento resultante, é necessário considerar a distância entre a força e o ponto em que se deseja calcular o momento.
Para calcular o momento de uma força em relação a um ponto específico, a fórmula é:
Momento = Força x Distância perpendicular ao ponto
É importante lembrar que o momento é uma grandeza vetorial e, portanto, possui direção e sentido. Para determinar a direção do momento resultante, é necessário utilizar a regra da mão direita.
Em resumo, o momento resultante em um sistema de forças pode ser calculado somando os momentos individuais de cada força que atua no sistema, levando em consideração a distância entre a força e o ponto em que se deseja calcular o momento.
Como calcular o momento escalar de uma força de maneira simples e eficaz.
Calcular o momento escalar de uma força é uma tarefa fundamental em física e engenharia. O momento escalar de uma força é o produto da força aplicada por sua distância ao ponto de rotação. Para calcular esse momento, você precisa conhecer a magnitude da força e a distância perpendicular entre a linha de ação da força e o ponto de rotação.
A fórmula para calcular o momento escalar de uma força é simples: Momento = Força x Distância. Para facilitar o cálculo, é importante garantir que a força e a distância estejam na mesma unidade de medida. Por exemplo, se a força é medida em Newtons e a distância em metros, o momento será dado em Newton-metros (Nm).
Para calcular o momento escalar de uma força em um sistema de várias forças, você deve calcular o momento de cada força individualmente e depois somá-los. Lembre-se de considerar a direção do momento (sentido horário ou anti-horário) ao somar os momentos das forças.
Praticar exercícios é fundamental para entender e aplicar os conceitos de momento escalar de uma força. Resolva problemas que envolvam diferentes forças atuando em diferentes pontos de um objeto, e lembre-se de considerar a direção e sentido de rotação em cada caso.
Em resumo, para calcular o momento escalar de uma força de maneira simples e eficaz, basta multiplicar a magnitude da força pela distância ao ponto de rotação. Pratique a resolução de exercícios para aprimorar suas habilidades e compreensão desse conceito fundamental em física e engenharia.
Momento de torção: características e fórmulas, exercícios
O torque , torque ou momento de uma força é a capacidade de uma força causar uma curva. Etimologicamente, recebe o nome torque como uma derivação da palavra inglesa torque , do latim torquere (twist).
O torque (em relação a um dado ponto) é a magnitude física resultante da produção do produto vetorial entre os vetores de posição do ponto em que a força é aplicada e a da força exercida (na ordem indicada). Este momento depende de três elementos principais.

O primeiro desses elementos é a magnitude da força aplicada, o segundo é a distância entre o ponto em que é aplicado e o ponto em que o corpo gira (também chamado de braço da alavanca) e o terceiro elemento é o ângulo de aplicação da referida força.
Quanto maior a força, maior a rotação. O mesmo se aplica ao braço da alavanca: quanto maior a distância entre o ponto em que a força é aplicada e o ponto em relação ao qual a curva é produzida, maior será.
Logicamente, o torque é de especial interesse na construção e na indústria, bem como em muitas aplicações domésticas, como quando você aperta uma porca com uma chave inglesa.
Fórmulas
A expressão matemática do torque de uma força em relação a um ponto O é dada por: M = rx F
Nesta expressão, r é o vetor que une o ponto de O ao ponto P da aplicação da força e F é o vetor da força aplicada.
As unidades de medida do momento são N ∙ m, que embora dimensionalmente iguais a julho (J), têm um significado diferente e não devem ser confundidas.
Portanto, o módulo de torque assume o valor fornecido pela seguinte expressão:
M = r ∙ F ∙ sen α
Nessa expressão, α é o ângulo entre o vetor de força e o vetor de braço de alavanca ro. O torque é considerado positivo se o corpo girar no sentido anti-horário; pelo contrário, é negativo quando gira no sentido horário.
Unidades
Como já mencionado acima, a unidade de medida do torque é o produto de uma unidade de força por uma unidade de distância. Especificamente, no Sistema Internacional de Unidades é usado o medidor de Newton cujo símbolo é N • m.
No nível dimensional, o medidor de Newton pode parecer equivalente a julho; No entanto, em nenhum caso julho deve ser usado para expressar momentos. Julho é uma unidade para medir trabalhos ou energias que, do ponto de vista conceitual, são muito diferentes dos momentos de torção.
Da mesma forma, o torque possui um caractere vetorial, que é tanto trabalho escalar quanto energia.
Caracteristicas
Segue-se que o momento de torcer uma força em relação a um ponto representa a capacidade de uma força ou conjunto de forças para modificar a rotação do referido corpo em torno de um eixo que passa através do ponto.
Portanto, o momento de torção gera uma aceleração angular no corpo e é uma magnitude do caractere vetorial (portanto, é definido a partir de um módulo, uma direção e um sentido) que está presente nos mecanismos que foram submetidos torção ou flexão.
O torque será nulo se o vetor de força e o vetor r tiverem a mesma direção, pois nesse caso o valor de sen α será nulo.
Torque resultante
Dado um certo corpo no qual uma série de forças atua, se as forças aplicadas atuam no mesmo plano, o torque resultante da aplicação de todas essas forças; É a soma do torque devido a cada força. Portanto, cumpre-se que:
H T = Σ M = M 1 + M 2 + H 3 + …
Evidentemente, é necessário levar em consideração os critérios dos sinais para os momentos de torção, conforme explicado acima.
Aplicações
O torque está presente em aplicações diárias, como apertar uma porca com uma chave inglesa, abrir ou fechar uma torneira ou uma porta.
No entanto, suas aplicações vão muito além; O torque também é encontrado nos eixos das máquinas ou no resultado das tensões às quais as vigas estão sujeitas. Portanto, suas aplicações na indústria e na mecânica são muitas e variadas.

Exercícios resolvidos
Abaixo estão alguns exercícios para facilitar a compreensão do que foi dito acima.
Exercício 1
Dada a figura a seguir, na qual as distâncias entre o ponto O e os pontos A e B são respectivamente 10 cm e 20 cm:
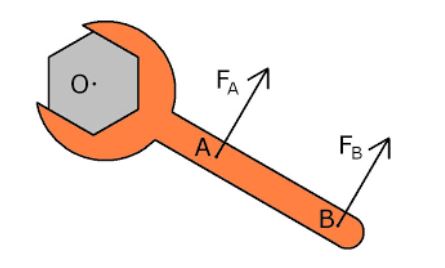
a) Calcule o valor do módulo de torque em relação ao ponto O se uma força de 20 N for aplicada no ponto A.
b) Calcule o valor da força aplicada em B para atingir o mesmo torque obtido na seção anterior.
Solução
Antes de tudo, é conveniente passar os dados para as unidades do sistema internacional.
r A = 0,1 m
r B = 0,2 m
a) Para calcular o módulo de torque, usamos a seguinte fórmula:
M = r ∙ F ∙ sen α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m
b) Para determinar a força solicitada, proceda de maneira semelhante:
M = r ∙ F ∙ sen α = 0,2 ∙ F ∙ 1 = 2 N ∙ m
Na compensação F, você obtém o seguinte:
F = 10 N
Exercício 2
Uma mulher exerce uma força de 20 N no final de uma chave de boca de 30 cm de comprimento. Se o ângulo da força com a alça da chave é de 30 °, qual é o torque na porca?
Solução
A seguinte fórmula é aplicada e operada:
M = r ∙ F ∙ sen α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m
Referências
- Momento de força. (nd) Na Wikipedia Recuperado em 14 de maio de 2018, em es.wikipedia.org.
- Torque (nd) Na Wikipedia Recuperado em 14 de maio de 2018, em en.wikipedia.org.
- Serway, RA e Jewett, Jr. JW (2003).Física para cientistas e engenheiros . 6ª Ed. Brooks Cole.
- Marion, Jerry B. (1996).Dinâmica clássica de partículas e sistemas . Barcelona: Ed. Eu inverti.
- Kleppner, Daniel; Kolenkow, Robert (1973).Uma introdução à mecânica . McGraw-Hill