Prodotto di frazioni: guida completa con esempi ed esercizi

Início » Ciência » Matemática » Prodotto di frazioni: guida completa con esempi ed esercizi

Capire davvero come trovare il prodotto di frazioni è una competenza che torna utile a scuola, negli esami e anche nella vita quotidiana quando si fanno conti proporzionali. La regola è semplice, ma saperla applicare con naturalezza richiede esempi, trucchi e buone abitudini di semplificazione, così da evitare errori e risparmiare tempo.

In questo articolo trovi una guida pratica e completa, scritta con un linguaggio chiaro e informale, per accompagnarti passo dopo passo. Dalla definizione ai segni, dalla moltiplicazione con numeri interi alle frazioni miste, passando per semplificazioni e “cancellazioni” intelligenti, qui c’è tutto quello che serve, con esercizi svolti e spiegati.

Cos’è il prodotto di frazioni e qual è la regola generale

Quando moltiplichiamo frazioni, non “sommiamo parti”, bensì costruiamo una nuova frazione che rappresenta il prodotto delle quantità coinvolte. La regola generale dice: si moltiplicano i numeratori tra loro e i denominatori tra loro. Non importa quante frazioni ci siano: la procedura resta identica.

Per esempio, se abbiamo 2/3 e 4/5, calcoliamo: 2 × 4 al numeratore e 3 × 5 al denominatore, ottenendo 8/15. Questa linearità vale anche con tre o più frazioni: si procede “in orizzontale” su tutti i numeratori e su tutti i denominatori.

Attenzione a non confondere la moltiplicazione con l’addizione o la sottrazione di frazioni. Nella somma/sottrazione si lavora sul denominatore comune, mentre nel prodotto non serve alcun denominatore comune: si moltiplica direttamente.

Un altro punto chiave: il valore 1 è l’elemento neutro della moltiplicazione. Questo dettaglio tornerà utile quando tratteremo numeri interi visti come frazioni con denominatore 1.

Un paio di esempi rapidi per fissare l’idea: 1/6 × 7/3 = (1 × 7)/(6 × 3) = 7/18. Oppure 3/2 × 5/1 = 15/2, che è già un esempio di prodotto tra frazione e intero.

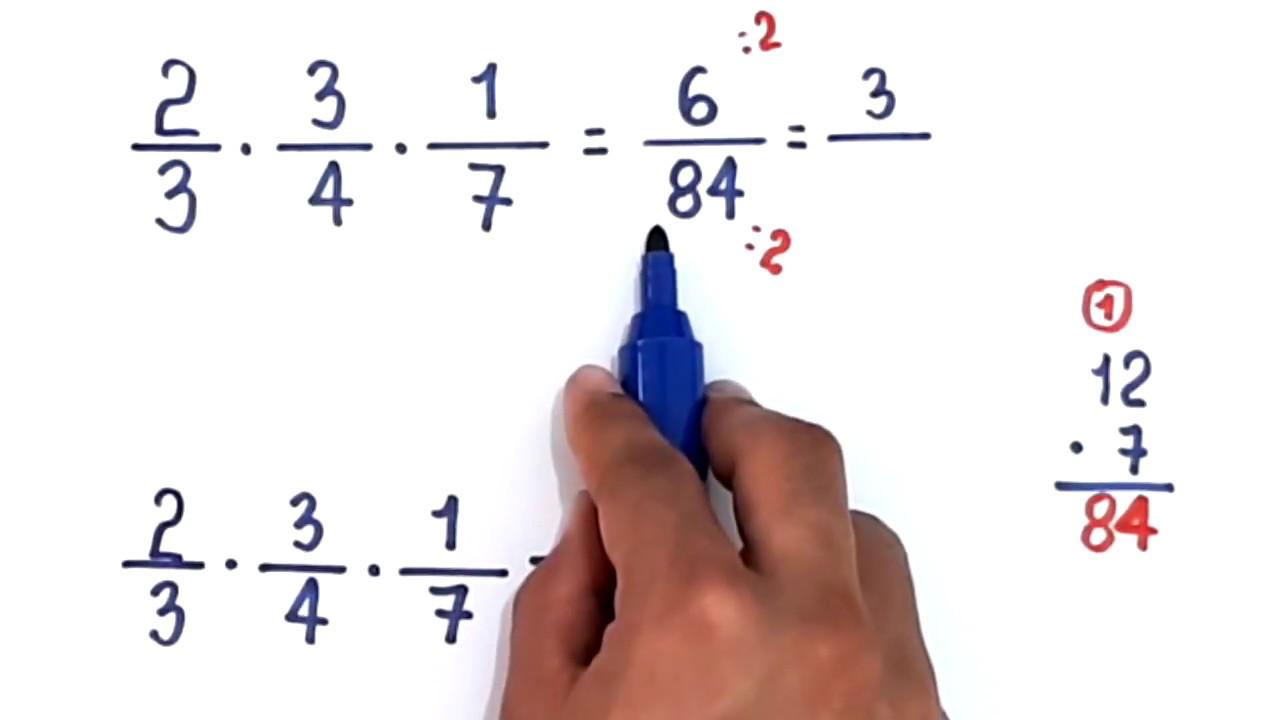
Dimostrazione intuitiva e ripasso dei termini: numeratore e denominatore

Per muoversi con sicurezza, è utile un piccolo ripasso. Il numeratore è il numero sopra la linea di frazione e indica quante parti consideriamo, mentre il denominatore è il numero sotto e indica in quante parti uguali è stato diviso l’intero.

Immagina un intero tagliato in 3 parti uguali: ogni parte è 1/3. Se prendi 2 parti, ottieni 2/3. Quando moltiplichi frazioni, stai prendendo “una frazione di una frazione”, e quindi è naturale che numeratori e denominatori si moltiplichino tra loro.

Questa interpretazione “a fette” spiega bene il meccanismo: se prendo 4/5 di un gruppo, e poi considero 2/3 di quel 4/5, il risultato è (2 × 4)/(3 × 5) = 8/15 dell’intero iniziale.

Ricorda anche che il denominatore non può essere zero, perché non si possono dividere oggetti in “zero parti”. Il vincolo “denominatore diverso da 0” è fondamentale in tutte le operazioni con frazioni.

Questa intuizione rende la regola immediata e giustifica perché la moltiplicazione di frazioni non richiede denominatore comune. Basta moltiplicare numeratori e denominatori e, se possibile, semplificare il risultato.

Moltiplicare una frazione per un numero intero

Moltiplicare una frazione per un intero è più semplice di quanto sembri. L’intero si considera come una frazione con denominatore 1. Per esempio, 5 diventa 5/1, 12 diventa 12/1, e così via.

Quindi 3/2 × 5 diventa 3/2 × 5/1 = (3 × 5)/(2 × 1) = 15/2. Nella pratica, spesso si moltiplica direttamente l’intero per il numeratore e si conserva il denominatore, quando l’intero è messo su 1.

Altro esempio: 12 × 2/5 = (12 × 2)/5 = 24/5. Se puoi semplificare prima, fallo: ad esempio, se avessi 12 × 5/6, si può “cancellare” 12 e 6 dividendo entrambi per 6, trasformando l’espressione in 2 × 5/1 = 10.

Questa strategia è molto efficiente nei calcoli a mente o su carta: riduci ai minimi termini prima di moltiplicare, ti eviti numeri grandi e semplificazioni finali pesanti.

Prodotto con denominatori uguali e con denominatori diversi

Nella moltiplicazione di frazioni, la presenza di denominatori uguali o diversi non cambia la procedura. Si moltiplicano comunque numeratori tra loro e denominatori tra loro, senza cercare denominatori comuni.

Con denominatori uguali, ad esempio 2/7 × 5/7 = (2 × 5)/(7 × 7) = 10/49. Non si “ripete il denominatore” come nella somma, perché qui la logica è differente.

Con denominatori diversi, per esempio 1/4 × 3/8 = (1 × 3)/(4 × 8) = 3/32. La regola resta identica e non richiede alcun lavoro preparatorio sui denominatori.

Un errore comune è trattare il prodotto come una somma. Ricorda: somma e sottrazione richiedono denominatore comune; moltiplicazione e divisione, no. Questo distingue nettamente i due tipi di calcolo.

Frazione mista per frazione: come procedere

Le frazioni miste hanno una parte intera e una frazionaria, per esempio 2 1/3. Per moltiplicare una frazione mista, converti prima in frazione impropria (numeratore maggiore del denominatore).

Passi pratici: 1) trasforma la frazione mista in impropria; 2) moltiplica come al solito; 3) semplifica se possibile. Esempio: 2 1/3 × 3/4. Prima converti 2 1/3 in 7/3 (perché 2 × 3 + 1 = 7), poi 7/3 × 3/4 = (7 × 3)/(3 × 4) = 21/12.

Ora semplifica: 21/12 ha un fattore comune 3 (21 ÷ 3 = 7, 12 ÷ 3 = 4), quindi diventa 7/4. Se vuoi, puoi tornare a frazione mista: 1 3/4. Spesso si preferisce lasciare la frazione impropria, specie in algebra.

Ricorda che la conversione a impropria è un passaggio obbligato per evitare errori. Moltiplicare direttamente una mista senza conversione porta quasi sempre a risultati sbagliati.

Regola dei segni nella moltiplicazione di frazioni

Le frazioni ereditano le regole del segno dai numeri interi. Prodotto di due numeri con lo stesso segno → risultato positivo; prodotto di due numeri con segni diversi → risultato negativo.

Esempi chiari: (−2/3) × 4/5 = −8/15, perché i segni sono diversi. Invece (−1/2) × (−1/3) = 1/6, poiché due segni negativi danno un risultato positivo.

Questa logica resta valida con più di due fattori: se il numero di segni negativi è pari, il risultato è positivo; se è dispari, è negativo. Tieni d’occhio i segni prima di semplificare.

Semplificazione delle frazioni: quando e come farla

Dopo aver moltiplicato, conviene quasi sempre verificare se la frazione ottenuta è riducibile. Se numeratore e denominatore hanno divisori comuni, puoi semplificare dividendo entrambi per lo stesso numero.

Esempio classico: 4/9 × 3/2 = 12/18. Sia 12 sia 18 sono divisibili per 6: ottieni 2/3. Questa è la forma irriducibile, cioè non si può semplificare ulteriormente.

Puoi semplificare anche prima di moltiplicare, quando vedi fattori in comune “in croce” o tra un numeratore e un denominatore. Questa strategia riduce i numeri e rende il calcolo più agile.

Trucchi per moltiplicare frazioni più velocemente

Eliminazione di fattori uguali

Se nelle frazioni compaiono lo stesso numero a numeratore e a denominatore (anche tra frazioni diverse), puoi “eliminarli” dividendo per loro stessi. È come semplificare prima del prodotto, evitando numeri grandi.

Esempio: (5/6) × (3/5). Il 5 al numeratore della prima e il 5 al denominatore della seconda si cancellano. Resta 3/6, che si semplifica a 1/2. Senza cancellazione avresti (5 × 3)/(6 × 5) = 15/30, poi semplificato a 1/2.

Metodo del “cancellamento” (semplificazione preventiva)

Oltre a eliminare fattori identici, puoi semplificare dividendo per un divisore comune numeri che si trovano “di traverso” (numeratore di una frazione e denominatore di un’altra). È il modo più efficiente per arrivare alla forma irriducibile.

Esempio: (9/5) × (15/6). Si può semplificare prima: 15 e 5 hanno fattore 5 → 15/5 = 3/1; 9 e 6 hanno fattore 3 → 9/6 = 3/2. Il prodotto diventa (3/1) × (3/2) = 9/2. È lo stesso risultato che otterresti calcolando 135/30 e poi riducendo, ma così si fa prima.

Altro esempio utile: (4/12) × (6/8). Dividi 4 e 12 per 4 → 1/3; dividi 6 e 8 per 2 → 3/4. Ora il prodotto è (1/3) × (3/4) = 1/4. Ridurre in anticipo evita frazioni grandi e passaggi in più.

Esercizi svolti e applicazioni pratiche

Qui trovi una selezione di esercizi tipici con soluzioni commentate. Allenati a riconoscere quando conviene semplificare prima e come gestire segni, interi e frazioni miste.

Esercizio 1: calcola il prodotto e scrivi l’inverso

Calcola (2/3) × (9/4). Soluzione: (2 × 9)/(3 × 4) = 18/12 = 3/2 dopo semplificazione (dividi per 6). L’inverso (reciproco) è 2/3. Ricorda: l’inverso di a/b è b/a, purché a e b siano non nulli.

Esercizio 2: percentuale di una collezione (frazione di un intero)

Susanna ha 12 smalti e 2/3 sono della marca Alfa. Quanti sono? Soluzione: 12 × 2/3 = (12 × 2)/3 = 24/3 = 8. Susanna possiede 8 smalti Alfa. Quando moltiplichi un intero per una frazione, pensa all’intero su 1 e semplifica subito se puoi.

Esercizio 3: scala su una mappa

La scala indica che 1 cm sul disegno corrisponde a 5 km reali. La distanza tra A e B sulla mappa è 12 cm: quanti chilometri separano le due città? Soluzione: 12 × 5 = 60 km

Se vuoi esprimerla come prodotto di frazioni: 12/1 × 5/1 = 60/1. Il ragionamento è identico, solo scritto in forma frazionaria.

Esercizio 4: prodotto di ragioni pari a 30

Si sa che (x/4) × (5/2) = 30. Trova x. Soluzione: (x × 5)/(4 × 2) = 30 → (5x)/8 = 30 → 5x = 240 → x = 48. Nei problemi algebrici, porta sempre la frazione in forma lineare e isola l’incognita.

Esercizio 5: musica e frazioni di tempo

In un brano con 8 battute in 3/4, quante unità di tempo totali ci sono? Soluzione: 8 × 3/4 = 24/4 = 6 unità di tempo

Verifica combinazioni equivalenti: 24 crome (1/8) e 12 semiminime (1/4) sommano a 6, perché 24 × 1/8 = 3 e 12 × 1/4 = 3; 3 + 3 = 6. Questo mostra come le frazioni descrivano perfettamente durate e proporzioni reali.

Esercizio 6: prodotto con segni

Calcola (−2/3) × (4/5) e (−1/2) × (−1/3). Soluzione: il primo dà −8/15 (segni diversi → negativo); il secondo dà 1/6 (due negativi → positivo). Controlla sempre i segni prima di semplificare.

Esercizio 7: frazione mista con semplificazione

Calcola 1 1/2 × 2/3. Trasforma la mista: 1 1/2 = 3/2. Prodotto: (3/2) × (2/3) = 6/6 = 1. Qui puoi “cancellare” 3 con 3 e 2 con 2 prima ancora di moltiplicare, arrivando subito a 1. Il metodo del cancellamento è potentissimo.

Domande frequenti e chiarimenti utili

Serve il denominatore comune per moltiplicare frazioni? No, il denominatore comune serve solo per sommare o sottrarre frazioni. Nel prodotto si moltiplicano numeratori e denominatori direttamente.

Posso semplificare prima di moltiplicare? Sì, ed è consigliabile. Riduci fattori comuni tra un numeratore e un denominatore, anche “in croce”, così il risultato sarà già vicino alla forma finale.

Come si trattano gli interi? Considerali come frazioni con denominatore 1, ad esempio 7 diventa 7/1. Questo consente di applicare senza sforzo la regola generale.

Cosa sono le frazioni equivalenti? Sono frazioni diverse che rappresentano lo stesso numero, come 12/18 e 2/3. Portare una frazione alla forma irriducibile ti dà la rappresentazione più semplice.

Esempi aggiuntivi per fare pratica

Esempio A: 2/3 × 4/5 = 8/15 (già irriducibile). Esempio B: 1/6 × 7/3 = 7/18. Qui nessun fattore comune da cancellare prima del prodotto.

Esempio C: 12 × 2/5 = 24/5. Esempio D: (4/9) × (3/2) = 12/18 = 2/3, dopo divisione per 6. Vedi come la semplificazione finale riduce ai minimi termini.

Esempio E: (9/5) × (15/6) → semplifica prima: 15/5 = 3 e 9/6 = 3/2; prodotto 3 × 3/2 = 9/2. Stesso risultato di (135/30) semplificato, ma con meno passaggi.

Esempio F: 2 1/3 × 3/4 = 7/3 × 3/4 → semplifica 3 con 3 → 7/4 → 1 3/4. Convertire correttamente la frazione mista è il primo passo da non sbagliare.

Consigli pratici per studiare con efficacia

Quando inizi, scrivi sempre tutto in colonna e senza salti, poi passa alla semplificazione preventiva. Se preferisci, evidenzia con una penna colorata i fattori comuni da “cancellare” tra numeratori e denominatori.

Nei problemi di testo, traduci la frase in un’espressione frazionaria prima di calcolare. Ad esempio, “i 2/3 di 12” significa 12 × 2/3; poi riduci 12/3 a 4 e moltiplica 4 × 2.

Evita di portare numeri enormi fino alla fine: semplifica non appena ne hai la possibilità. È un’abitudine che migliora accuratezza e velocità, soprattutto negli esercizi con più fattori.

Controlla sempre i segni e, se l’esercizio lo richiede, esprimi il risultato in forma irriducibile o come frazione mista. La forma richiesta dal problema è parte della risposta corretta.

La moltiplicazione di frazioni non ha nulla di misterioso: si tratta di applicare una regola lineare (numeratore con numeratore, denominatore con denominatore), curando segni e semplificazioni. Con un po’ di pratica, frazioni miste, interi, cancellazioni e verifica dell’irriducibilità diventano gesti automatici, e quegli esercizi che sembravano “spigolosi” iniziano a scorrere con naturalezza.