Como posicionar frações em uma reta numérica: do básico ao avançado

Início » Ciência » Matemática » Como posicionar frações em uma reta numérica: do básico ao avançado

Se a sua dúvida é como colocar uma fração no lugar certo de uma reta numérica, você chegou ao ponto certo. A reta numérica é um mapa perfeito para visualizar números racionais, porque mostra claramente onde cada fração fica em relação aos inteiros e à sua localização de números inteiros e decimais, tanto à direita (positivos) quanto à esquerda (negativos). A ideia central é simples: cada fração representa uma parte da unidade, então sua posição está entre marcas inteiras contíguas, como entre 0 e 1, entre 1 e 2, e assim por diante.

Antes de desenhar qualquer pontinho na reta, vale firmar a base. Quando escrevemos uma fração no formato a/b, o número de cima é o numerador e o de baixo é o denominador. O denominador indica em quantas partes iguais cada unidade é dividida; o numerador conta quantas dessas partes estamos considerando, começando do zero e deslocando-se para a direita se for positivo (ou para a esquerda, se for negativo).

O que é a reta numérica e como ela ajuda com frações

Uma reta numérica é uma linha com marcações igualmente espaçadas que representam os números inteiros em ordem crescente e decrescente. O zero fica no centro como referência (curiosidades sobre o número zero), os positivos à direita e os negativos à esquerda. Entre cada par de inteiros consecutivos (por exemplo, entre 0 e 1) cabe um número infinito de frações, pois podemos dividir o intervalo em tantas partes iguais quanto o denominador pedir.

Essa estrutura faz da reta numérica um recurso visual poderoso. Ao dividir o segmento entre dois inteiros de acordo com o denominador, a posição exata da fração surge naturalmente, sem precisar de cálculos complicados. É uma maneira clara de comparar, ordenar e compreender grandezas.

Outro ponto crucial é o espaçamento. As marcas na reta precisam ser uniformes, porque cada unidade é congruente com a seguinte; isso garante que o “tamanho” de um passo não mude de 0 a 1 ou de 5 a 6. Sem essa regularidade, a leitura de frações fica enganosa.

Além disso, a reta permite observar relações importantes como simetria. Para qualquer fração positiva a/b, a fração negativa −a/b fica à mesma distância do zero, só que do lado esquerdo. Esse espelhamento é essencial para entender sinais e magnitude; veja o valor absoluto e relativo.

Entendendo a notação a/b: numerador e denominador

Quando escrevemos a/b, interpretamos: “divida cada unidade em b partes iguais e conte a dessas partes a partir do zero”. O denominador b determina o tamanho do “pedaço” de unidade; o numerador a diz quantos pedaços serão tomados. Se a/b for maior que 1 (ou seja, a ≥ b), caminharemos além do primeiro inteiro, e se a/b for menor que 1 (a < b), ficaremos entre 0 e 1.

Um exemplo clássico é 3/2. Como o denominador é 2, dividimos cada unidade (por exemplo, de 0 a 1 e de 1 a 2) em duas partes iguais; o numerador 3 indica que avançamos três dessas meias unidades a partir do zero, ou seja, passamos de 0 a 1 (duas metades) e depois até a metade seguinte, parando em 1 e 1/2. Assim, 3/2 está entre 1 e 2, exatamente no meio entre 1,5 e 2.

Com frações próprias (a < b), a posição fica sempre dentro de um único intervalo unitário. Já com frações impróprias (a ≥ b), ultrapassamos pelo menos um inteiro e, muitas vezes, expressá-las como número misto ajuda a visualizar. Por exemplo, 7/4 = 1 + 3/4; entendemos rapidamente que está entre 1 e 2, próximo de 2.

Essa leitura da notação a/b vale para qualquer racional, inclusive negativos; consulte a classificação de números reais. O sinal “−” não muda o tamanho do pedaço, apenas o sentido em que caminhamos na reta: em vez de ir para a direita, vamos para a esquerda a mesma quantidade.

Como localizar frações próprias (0 < a/b < 1)

Para uma fração própria, olhamos o intervalo entre 0 e 1 (ou entre n e n+1, se estivermos comparando deslocamentos em outras regiões). Dividimos o segmento em b partes iguais e contamos a dessas partes a partir do zero. Por exemplo, 3/4 fica no terceiro ponto entre 0 e 1 quando dividimos esse trecho em quatro.

Vamos a mais ilustrações. Em 1/2, o denominador 2 indica que o intervalo é cortado ao meio, então a marca está exatamente no meio entre 0 e 1. Em 5/6, dividimos o intervalo em seis e paramos na quinta marca; fica próximo de 1, porque 5/6 é maior que 3/4 e 2/3.

É útil comparar frações no mesmo “grid”. Se quisermos visualizar 2/3 e 3/4 ao mesmo tempo, podemos dividir o intervalo entre 0 e 1 em 12 partes (mínimo múltiplo comum de 3 e 4). Assim, 2/3 vira 8/12 e 3/4 vira 9/12; imediatamente enxergamos que 3/4 é ligeiramente maior, pois fica uma marca adiante.

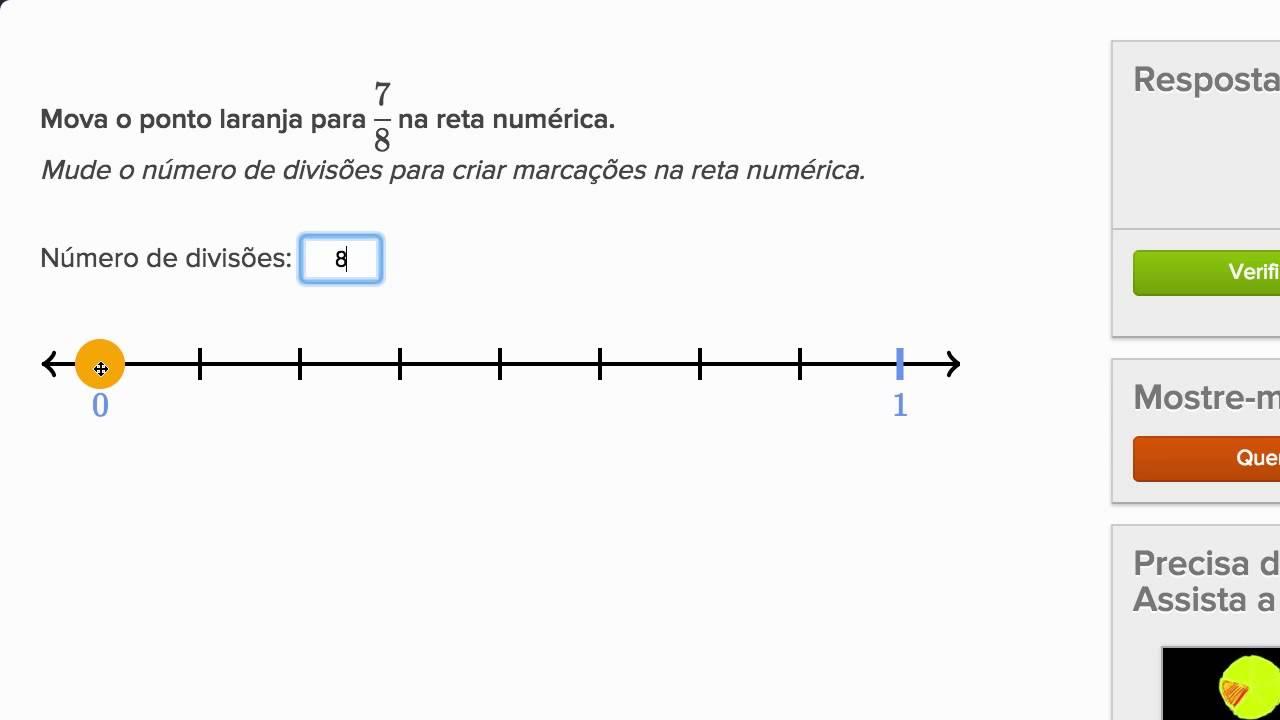
Para uma fração como 5/8, o processo não muda. Criamos oito divisões iguais e contamos até a quinta. A visão se torna natural com a prática: basta lembrar que o denominador dita quantas fatias tem a unidade, e o numerador diz quantas fatias usamos.

Frações impróprias e números mistos na reta

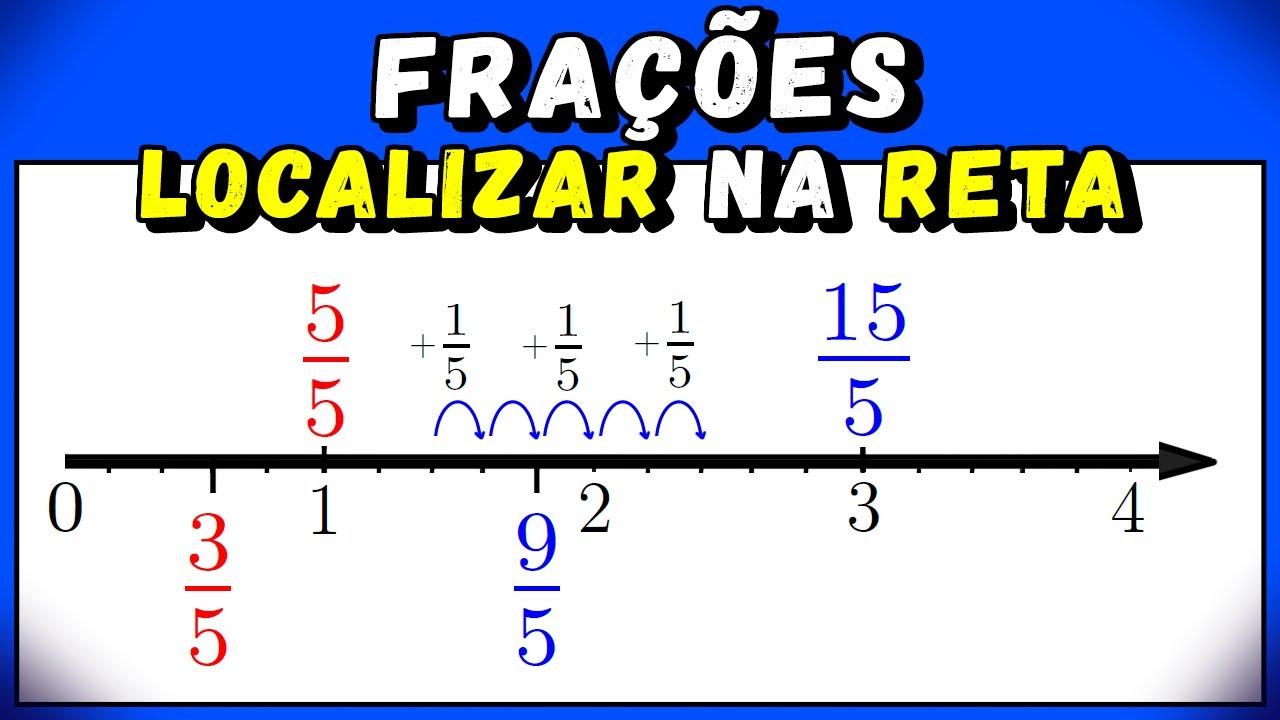
Frações impróprias (a ≥ b) ultrapassam pelo menos um inteiro. Para posicioná-las, ande inteiros completos e depois o resto da fração. Converter em número misto facilita: 3/2 = 1 + 1/2, 7/4 = 1 + 3/4, 9/5 = 1 + 4/5 e por aí vai.

Veja 3/2: primeiro avançamos uma unidade (de 0 a 1), depois tomamos mais 1/2 unidade, parando no ponto 1,5. Para 7/4, passamos por 1 inteiro e somamos 3/4, ficando três quartos do caminho entre 1 e 2.

Se a fração tiver numerador muito maior que o denominador, percorremos vários inteiros. Por exemplo, 17/6 = 2 + 5/6: saltamos de 0 a 2 (duas unidades completas) e, em seguida, contamos 5/6 do trecho até 3. Essa decomposição ajuda a manter a escala correta.

Nos negativos, o raciocínio é idêntico, mas para a esquerda. Assim, −3/2 fica à mesma distância que 3/2 em relação ao zero, porém no lado negativo da reta. É como um espelho: tudo que fizemos à direita tem par correspondente à esquerda com sinal trocado.

Do zero aos inteiros: onde a fração “cabe”

Uma dica prática para qualquer fração positiva é encontrar os inteiros vizinhos entre os quais ela se encaixa. Se a/b estiver entre n e n+1, então n ≤ a/b < n+1. Para achar n, basta dividir: n é a parte inteira de a/b.

Com isso, sabemos em qual intervalo dividir. Entre n e n+1, novamente partimos o segmento em b pedaços iguais e contamos a − n·b pedaços (porque já avançamos n unidades inteiras). Esse método unifica frações próprias e impróprias.

Exemplo: 11/4. A parte inteira de 11/4 é 2 (pois 11/4 = 2 + 3/4), então está entre 2 e 3. Dividimos apenas o segmento de 2 a 3 em quatro partes e vamos até a terceira marca; isso evita sobrecarregar toda a reta com divisões desnecessárias.

Para ajustes finos, rascunhe uma escala parcial. Se o objetivo é localizar 29/10, foque entre 2 e 3 (porque 29/10 = 2,9), coloque 10 divisões e marque a nona. Visualmente, fica nítido que está bem próximo de 3.

Sinais e simetria: frações negativas

Frações negativas seguem o mesmo tamanho de passo, só mudam de direção. Para −a/b, dividimos a unidade em b partes e contamos a para a esquerda. É vantajoso localizar primeiro a positividade de a/b, mentalmente, e espelhar em relação ao zero.

Por exemplo, −5/6. Sabendo que 5/6 fica quase encostado em 1, colocamos o ponto equivalente quase encostado em −1, do lado esquerdo. Essa visão espelhada acelera comparações: −3/4 está “mais à direita” do que −5/6, porque −0,75 é maior que −0,833…

Em contextos aplicados, o sinal é crucial. Se uma dívida é de 3/2 unidades, a posição correta na reta é à esquerda do zero, em −1,5. Ignorar o sinal é um erro comum que distorce a interpretação.

Por fim, ao comparar negativos, lembre-se: quanto mais à direita, maior é o número, mesmo do lado negativo. Assim, −1/4 é maior que −1/2, pois −0,25 fica mais próximo de zero do que −0,5.

Frações equivalentes e simplificação na reta

Duas frações equivalentes ocupam o mesmo ponto da reta. 3/4, 6/8 e 9/12, apesar de escritas diferentes, representam a mesma quantidade, então coincidem no mesmo lugar entre 0 e 1. Isso é visível quando redividimos o intervalo com um denominador comum.

Para comparar frações com denominadores distintos, um truque visual é usar o mínimo múltiplo comum. Se quisermos ver onde 2/3 e 5/6 caem exatamente, dividir o intervalo em 6 ou 12 pedaços torna a comparação imediata. 2/3 vira 4/6 e 5/6 já está pronto; observamos a ordem sem cálculos pesados.

Na prática, simplificar antes de marcar pode ajudar. Frações como 8/12 ficam mais fáceis de posicionar se as reduzirmos para 2/3. A posição é a mesma, mas o denominador menor facilita contar as subdivisões.

Mesmo assim, quando o objetivo é comparar muitas frações ao mesmo tempo, usar um único “grid” com denominador comum evita desenhar subdivisões diferentes em cada intervalo. Isso mantém a reta limpa e legível.

Densidade dos racionais: sempre cabe mais uma fração

Entre dois números racionais quaisquer, existe outro racional. Essa propriedade de densidade significa que sempre podemos refinar a malha de subdivisões e inserir novas frações entre as já marcadas. Por isso, a reta numérica é um modelo contínuo que acolhe infinitas marcas potenciais.

Para ensino e estudo, escolhemos um nível de precisão conveniente. Se estamos trabalhando com quartos, oitavos ou décimos, a malha escolhida determina o quanto conseguimos “ver” com nitidez. Quanto mais densa a malha, maior a precisão — mas menor a clareza visual, se exagerarmos.

Um bom equilíbrio é essencial. Selecione denominadores que façam sentido para o conjunto de frações em análise, sem deixar o desenho poluído. Em tarefas diferentes, ajuste a densidade conforme a necessidade.

Essa perspectiva também explica por que diferentes representações decimais podem aparecer. Por exemplo, 1/3 não tem decimal finito; ainda assim, a posição na reta é precisa via subdivisões ternárias, e aproximamos em decimal conforme a precisão que quisermos.

Decimais como frações na reta

Todo decimal finito é uma fração. 0,75 é 75/100, que simplifica para 3/4; 0,2 é 1/5; 1,25 é 5/4. Marcar decimais na reta é, na prática, o mesmo que marcar frações equivalentes.

Essa equivalência é útil para comparar formas mistas de escrita. Se uma pessoa fala 0,6 e outra fala 3/5, ambas apontam para o mesmo ponto. A reta mostra essa identidade visualmente.

Quando os decimais não são finitos, recorremos a frações para posicionar com exatidão. Para 0,333…, usamos 1/3. Para 0,142857…, usamos 1/7, e assim por diante. A reta aceita os dois pontos de vista sem contradição.

Em problemas de medida, é comum alternar entre as formas. Se uma distância é 1,5 unidade, escrevê-la como 3/2 pode simplificar operações com outras frações, mantendo a consistência da malha na reta.

Erros comuns ao posicionar frações e como evitar

Alguns enganos aparecem com frequência e atrapalham a leitura. Evitar esses deslizes ajuda a construir representações confiáveis:

• Intervalos desiguais: desenhar 0-1 com um tamanho e 1-2 com outro muda a escala; mantenha a mesma unidade visual ao longo da reta.
• Contagem errada das subdivisões: o denominador b pede exatamente b partes iguais; não conte as marcas, conte os espaços entre marcas.
• Ignorar o sinal: uma fração negativa deve ir para a esquerda do zero; posicioná-la à direita inverte o sentido do problema.
• Confundir numerador com denominador: o de baixo diz “em quantas partes a unidade foi dividida”; o de cima diz “quantas dessas partes pegamos”.
• “Pular” inteiros em frações impróprias: converta em número misto para localizar em qual intervalo n a n+1 a parte fracionária cai.

Uma boa prática é checar a razoabilidade. Se a fração é maior que 1/2, ela deve estar mais perto de 1 do que de 0. Se for 7/8, por exemplo, não pode estar no começo do intervalo; o posicionamento deve refletir a grandeza.

Outra dica é usar rascunhos locais. Em vez de dividir toda a reta, foque apenas no intervalo onde a fração se encontra. Isso dá clareza e rapidez, especialmente com denominadores altos.

Quando várias frações aparecem juntas, padronize. Escolher um denominador comum para o intervalo permite comparar posições sem redesenhar malhas diferentes. A leitura coletiva fica muito mais limpa.

Por fim, treine com diferentes sinais e tamanhos. Alternar entre próprias, impróprias, mistas e negativas fortalece a intuição e evita armadilhas quando os exercícios variam o contexto.

Exemplos práticos detalhados

Exemplo 1: 3/8. Divida o intervalo 0-1 em 8 partes iguais e marque na terceira. Visualmente, fica um pouco antes de 1/2, já que 4/8 = 1/2.

Exemplo 2: 5/3. Converta para 1 + 2/3. Caminhe uma unidade inteira (0 a 1) e, no intervalo 1-2, divida em três; pare na segunda marca. O ponto fica mais perto de 2 do que de 1.

Exemplo 3: −7/4. Converta para −(1 + 3/4). No lado esquerdo, vá até −1 e, do intervalo −1 a −2, divida em quatro, parando na terceira subdivisão a partir de −1 em direção a −2. É o simétrico de +7/4 em relação ao zero.

Exemplo 4: comparação entre 2/5 e 3/10. Use denominador comum 10: 2/5 = 4/10, então 4/10 < 3/10? Não: 4/10 é maior que 3/10. Na reta, 3/10 está um pouco antes de 1/3, 4/10 está exatamente em 0,4.

Exemplo 5: localização de 29/12. Divida: 29/12 = 2 + 5/12. Vá até 2; no intervalo 2-3, crie 12 partes iguais e marque a quinta. Está um pouco antes de 2,5, pois 6/12 seria 1/2.

Aplicações e conexões com problemas reais

Medidas, tempo, dinheiro e proporções aparecem o tempo todo. Se um percurso é de 3/2 quilômetro, na reta isso está em 1,5, reforçando que passamos da unidade. Essa visualização auxilia na interpretação e em operações posteriores.

Em culinária, 3/4 de xícara é facilmente comparável a 2/3 de xícara no traço da reta. Ao adotar um denominador comum (12), 3/4 vira 9/12 e 2/3 vira 8/12, e vemos que 3/4 é um pouquinho maior — detalhe que faz diferença em receitas delicadas.

Em finanças, saldos positivos e negativos se beneficiam da simetria. Um crédito de 1/2 e um débito de −1/2 têm a mesma magnitude, mas efeitos opostos. A reta ajuda a não confundir ganhos com perdas quando frações surgem na análise.

Na física, deslocamentos e variações podem ser fracionários. Marcar 5/6 de metro no sentido positivo e −5/6 no negativo mostra direções distintas com a mesma intensidade. É uma ponte direta entre matemática e fenômenos do mundo real.

Até em estatística descritiva informal, proporções aparecem a toda hora. Ver 3/10 da turma escolhendo uma opção e 2/5 (4/10) preferindo outra é imediato na reta, evitando equívocos de percepção.

Rotina de estudo: fortalecendo a intuição

Para dominar o tema, é bom criar uma rotina curta e focada. Escolha diariamente três frações: uma própria, uma imprópria e uma negativa, e marque na reta. Em poucos dias, a habilidade fica automática.

Varie os denominadores. Pratique com terços, quartos, quintos, sextos, oitavos e décimos. Depois misture em conjuntos para treinar a ideia de denominador comum visual.

Invente microdesafios de comparação. Sem calcular, tente decidir qual é maior apenas “olhando” a posição esperada. Em seguida, confirme com uma conversão para o mesmo denominador.

Por último, anote dúvidas recorrentes. Se notar tropeços com sinais ou conversão para número misto, crie exemplos específicos até que o processo fique natural. A prática intencional corrige vícios rapidamente.

Todo esse percurso gira em torno de uma ideia central: os números racionais representam frações da unidade, e sua posição na reta nasce de dividir cada intervalo inteiro em partes iguais segundo o denominador e contar quantas partes o numerador indica. Com essa chave em mãos, localizar 3/2, 7/4, 5/8 ou −9/5 vira um procedimento tranquilo e previsível.