Como somar e subtrair frações impróprias passo a passo

Início » Ciência » Matemática » Como somar e subtrair frações impróprias passo a passo

Somar e subtrair frações impróprias não precisa ser um bicho de sete cabeças: quando você entende como alinhar os denominadores e manipular os numeradores, tudo flui de maneira natural. Neste guia, vamos organizar as ideias com clareza, do significado de cada termo ao passo a passo prático com MMC, exemplificando com números reais e mostrando quando e como simplificar os resultados.

Ao longo do texto, você verá que frações impróprias aparecem o tempo todo: em receitas, medições, problemas de proporções, estatística e até em equações algébricas. Também vamos mostrar por que elas são um atalho útil para números mistos e como se relacionam com operações de multiplicação e divisão em contextos do dia a dia e acadêmicos.

O que é uma fração imprópria e como reconhecê-la

Uma fração é dita imprópria quando o numerador é maior ou igual ao denominador; em termos práticos, seu valor é pelo menos 1. Exemplos clássicos são 7/3, 5/3 ou 10/9, todas maiores do que um inteiro (ou exatamente 1 quando o numerador e o denominador são iguais).

Para identificar rapidamente, basta comparar numerador e denominador: se o de cima for maior ou igual ao de baixo, temos uma fração imprópria; se for menor, a fração é própria. Essa “checagem-relâmpago” ajuda muito quando você está organizando termos antes de somar ou subtrair.

Outro ponto essencial é entender o vocabulário: numerador é o número da parte superior e denominador é o da parte inferior. Essa noção simples permite ler e interpretar qualquer fração corretamente, além de dar segurança quando a atividade envolve reescrever frações com denominadores equivalentes.

Por serem iguais ou superiores a 1, as frações impróprias podem ser convertidas em números mistos, isto é, na forma “parte inteira + fração”. Por exemplo, 5/3 também pode ser escrito como 1 2/3, e 7/4 como 1 3/4. Em muitas situações, alternar entre a forma imprópria e a forma mista torna as contas e a leitura de resultados mais confortáveis.

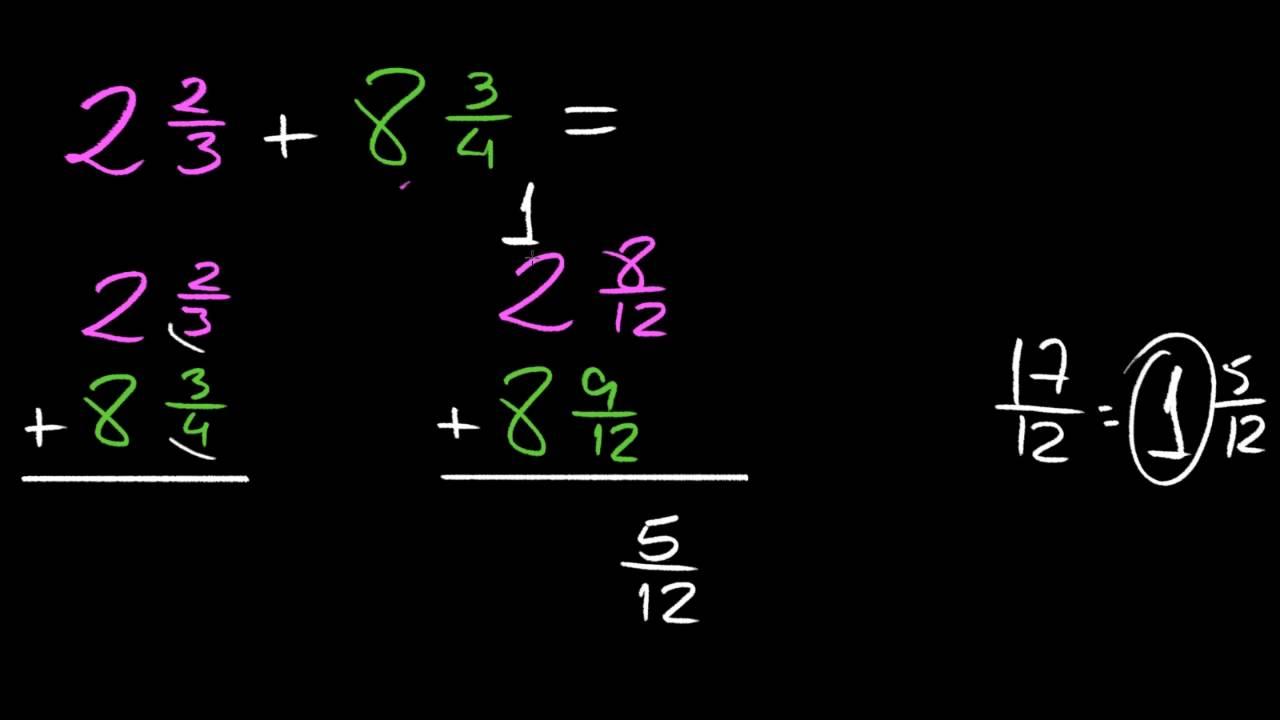
Como somar e subtrair: denominadores iguais e diferentes

Quando as frações envolvidas têm denominadores iguais, a regra é direta: somam-se ou subtraem-se os numeradores e mantém-se o denominador. Se você tem 13/7 + 5/7, por exemplo, some 13 e 5 para obter 18/7; se for 13/7 − 5/7, subtraia os numeradores e mantenha o 7.

O cenário muda quando os denominadores são diferentes. Nesse caso, é necessário torná-los iguais usando o mínimo múltiplo comum (MMC). O MMC é o menor número que é múltiplo dos denominadores envolvidos, e ele funciona como a “base comum” para reescrever as frações sem alterar seus valores.

O processo para somar ou subtrair com denominadores distintos é sistemático: 1) encontre o MMC; 2) divida o MMC por cada denominador para achar o fator de equivalência; 3) multiplique esse fator pelo numerador correspondente; 4) com os denominadores agora iguais, some ou subtraia os numeradores; 5) por fim, simplifique a fração resultante, se houver um divisor comum entre numerador e denominador.

Um detalhe importante: simplificar significa dividir numerador e denominador pelo mesmo número inteiro diferente de zero, buscando reduzir a fração à menor forma equivalente. Essa etapa não altera o valor, apenas deixa o resultado mais “enxuto” e, muitas vezes, mais fácil de interpretar.

MMC na prática: exemplos detalhados, passo a passo

Para consolidar a ideia, vamos a um caso clássico com três denominadores distintos. Se os denominadores forem 7, 8 e 5, o MMC é 280. Por quê? Porque 280 é o menor número que é múltiplo de 7, 8 e 5 simultaneamente.

Depois de achar o MMC, dividimos 280 por cada denominador para descobrir o fator que iguala as frações. Assim, 280/7 = 40, 280/8 = 35 e 280/5 = 56. Esses fatores indicam quanto devemos multiplicar os numeradores originais para reescrever as frações com denominador 280.

Suponha um conjunto com numeradores 32, 19 e 23 sobre 7, 8 e 5, respectivamente. Multiplicando cada numerador pelo fator correspondente, obtemos: 40 × 32 = 1280; 35 × 19 = 665; 56 × 23 = 1288. A partir daí, as frações já estão em base comum (denominador 280) e podem ser somadas ou subtraídas conforme a necessidade.

Outro exemplo útil aparece quando os denominadores são 9 e 2, cujo MMC é 18. O raciocínio é o mesmo: 18/9 = 2 e 18/2 = 9. Se os numeradores forem 25, 20 e 42 (em uma combinação de frações com esses denominadores, como 25/9, 20/2 e 42/2), multiplicamos 25 × 2 = 50; 20 × 9 = 180; 42 × 9 = 378 para reescrever cada uma sobre 18.

Quando o resultado surgir, é comum que ele permita simplificação. Se, por exemplo, a conta produzir algo do tipo 248/18, podemos dividir numerador e denominador por 2 e obter 124/9. Aí está a simplificação: reduzir a fração pelo seu divisor comum torna a escrita mais simples e elegante, sem alterar o valor numérico.

Somas e subtrações com números específicos

Vamos somar duas frações impróprias bem conhecidas: 5/3 + 7/4. O MMC de 3 e 4 é 12. Reescrevendo: 5/3 = 20/12 e 7/4 = 21/12. Somando os numeradores, 20 + 21 = 41, obtemos 41/12, que continua sendo uma fração imprópria. Se preferir, você pode expressá-la como número misto: 3 5/12.

Na subtração, a lógica é idêntica. Considere 5/3 − 3/2. O MMC de 3 e 2 é 6. Reescrevendo: 5/3 = 10/6 e 3/2 = 9/6. Agora, 10 − 9 = 1, resultando em 1/6. Note como duas frações impróprias podem produzir uma fração própria após a subtração, porque a diferença entre as partes pode ser menor do que um inteiro.

Com denominadores iguais, o procedimento fica mais curto. Em expressões como a/b + c/b ou a/b − c/b, basta mexer nos numeradores a e c e manter o denominador b. Ainda assim, vale conferir no final se existe uma simplificação possível dividindo ambos por algum fator comum.

Em situações com mais de duas frações, mantenha a disciplina: encontre o MMC de todos os denominadores, transforme cada parcela para a base comum e só então efetue a soma ou a subtração. Esse roteiro evita erros de reescrita e garante que ninguém “pise na bola” ao comparar números que estavam originalmente em bases diferentes.

Para fechar esta rodada de exemplos, lembre-se de que, ao reescrever e somar frações, o denominador comum é a chave. Ele garante que você esteja comparando “fatias do mesmo tamanho”, algo essencial quando pretende agregar ou retirar partes do todo.

Multiplicação, divisão e o papel das frações impróprias

Embora nosso foco seja somar e subtrair, o conteúdo se completa quando lembramos das outras operações. Na multiplicação de frações, multiplicamos numerador por numerador e denominador por denominador. Por exemplo, 5/3 × 2/3 = 10/9, outra fração imprópria que também pode ser expressa como 1 1/9.

Na divisão, o truque é multiplicar pela fração inversa: dividir por 2/3 equivale a multiplicar por 3/2. Assim, 5/3 ÷ 2/3 = (5/3) × (3/2) = 15/6, e simplificando por 3, fica 5/2. Perceba como os resultados continuam coerentes com os valores envolvidos e, muitas vezes, uma simplificação final dá o toque de qualidade ao resultado.

Essa visão ampla ajuda a perceber que frações impróprias são peça de ligação entre diferentes formas numéricas (misto, decimal) e entre operações diversas, mantendo a consistência matemática em qualquer direção que você siga.

Dicas rápidas e erros comuns para evitar

Uma dica de ouro é sempre verificar se há simplificação possível no fim da conta. Às vezes, o resultado surge “grande” porque ainda não foi reduzido; depois de dividir por um divisor comum, fica claro que a resposta era mais simples do que parecia.

Outro cuidado: quando for comparar frações ou tentar somá-las sem converter para denominadores iguais, não caia na tentação de somar denominadores diferentes diretamente. Isso distorce as proporções e gera resultados incorretos. O MMC existe justamente para equalizar as bases.

Por fim, sempre que possível, faça a checagem com a forma mista ou decimal, especialmente em contextos práticos (como medidas em receitas ou obras), pois a leitura muitas vezes fica mais intuitiva e você detecta inconsistências com mais facilidade.

Aplicações no cotidiano, na ciência e na engenharia

Frações impróprias aparecem em várias áreas: na física e na engenharia, representam medições acumuladas e relações entre grandezas; na estatística, podem surgir em cálculos de médias e proporções; e, na culinária, ajudam a ajustar receitas para mais ou menos porções sem perder a precisão.

Em medições — comprimento, tempo, volume — é comum que a soma de segmentos ou etapas gere valores acima da unidade, resultando em frações impróprias que depois podem ser convertidas em números mistos para facilitar a interpretação. É uma forma prática de manter exatidão e, ao mesmo tempo, comunicar o resultado de uma maneira amigável.

Na escola, dominar frações impróprias dá confiança aos estudantes. Elas são um passo natural rumo a números mistos e decimais, abrindo portas para conteúdos como equações algébricas, problemas de proporções e operações mais avançadas com expressões racionais.

Esse conhecimento também é valorizado em avaliações e atividades de projeto, em que a clareza na passagem entre diferentes representações — imprópria, mista, decimal — otimiza a resolução de problemas e minimiza erros de leitura ou arredondamento.

Um breve olhar histórico

O uso de frações (e, por extensão, impróprias) remonta a civilizações antigas. Os egípcios, por exemplo, já faziam medições fracionárias, ainda que com convenções diferentes das atuais. Com o avanço da matemática no mundo árabe e europeu durante a Idade Média, a noção moderna de frações foi sendo consolidada.

Entre os nomes que deixaram marca, Al-Khwarizmi e Fibonacci contribuíram para difundir procedimentos algébricos e o uso prático das frações em problemas de comércio, astronomia e outras áreas. Essa evolução histórica sedimentou o terreno para o modo como hoje ensinamos e usamos frações, próprias e impróprias, na escola e na vida cotidiana.

Essa trajetória mostra que as frações impróprias não são apenas um conteúdo escolar: elas fazem parte da linguagem universal da medida e da proporção, ajudando a descrever o mundo com precisão e eficiência.

Vocabulário essencial para não se perder

Frações impróprias: frações cujo numerador é maior ou igual ao denominador; valor maior ou igual a 1.

Frações próprias: numerador menor que o denominador; valor entre 0 e 1.

Números mistos: combinação de parte inteira com uma fração própria (como 1 3/4) que corresponde a uma fração imprópria equivalente.

Soma e subtração: operações que exigem denominador comum; a soma/subtração ocorre nos numeradores após a conversão.

Mínimo múltiplo comum (MMC): menor número que é múltiplo comum de todos os denominadores envolvidos.

Multiplicação e divisão de frações: multiplicar numerador por numerador e denominador por denominador; dividir é multiplicar pela fração inversa.

Proporções e medidas: relações e quantidades que frequentemente exigem frações para expressar resultados exatos.

Equações algébricas: expressões com frações que podem se beneficiar da forma imprópria para simplificar a manipulação.

Exercícios comentados

Questão 1

Realize as operações abaixo e, quando couber, simplifique o resultado dividindo por fatores comuns.

a) Somar três frações com denominadores distintos, usando MMC para igualar as bases e somar apenas os numeradores na sequência; a etapa final é verificar se há simplificação possível para tornar a resposta mais legível e direta.

b) Subtrair duas frações impróprias com denominadores diferentes, lembrando que o denominador comum deve ser encontrado antes e que a subtração acontece no topo, mantendo a base comum.

c) Em um conjunto de três frações, reescrever todas no denominador comum e somar; se aparecer um resultado como 248/18, divida por 2 e obtenha 124/9, garantindo a forma simplificada.

Questão 2

Uma barra de chocolate tem oito quadradinhos. Ontem foram consumidos três, hoje dois. Que fração foi consumida e qual ainda resta? A soma 3/8 + 2/8 = 5/8, logo já foram comidos 5/8 e restam 3/8. Essa leitura direta, com denominadores iguais, economiza tempo e evita confusões.

Questão 3

Ana tem 6 ovos e fará duas receitas: precisa de metade para o bolo e de um terço para a omelete. Metade de 6 é 3 e um terço de 6 é 2; somando 3 + 2 = 5 ovos ao todo. Essa é uma aplicação típica de frações em medidas e quantidades inteiras.

Ensino, ferramentas e boas práticas

Em sala de aula e em materiais didáticos, jogos, softwares e atividades práticas ajudam a visualizar frações e tornam a passagem entre formas impróprias, mistas e decimais mais natural. Visualizações e exercícios graduais constroem a intuição com segurança.

Docentes experientes e com formação específica em Matemática vêm ampliando o repertório de estratégias desde meados dos anos 2000, combinando teoria e prática em recursos online e presenciais. O resultado é um aprendizado mais envolvente e sólido, que prepara o estudante para desafios reais.

Para além da escola, a clareza na comunicação de resultados — escolhendo quando usar forma mista ou imprópria — facilita a colaboração entre áreas técnicas e não técnicas. Em relatórios, projetos e receitas, isso traz precisão sem perder legibilidade.

Se você reuniu todos esses pontos — vocabulário, MMC, equivalência e simplificação —, somar e subtrair frações impróprias vira rotina. Do 5/3 + 7/4 ao ajuste de porções na cozinha, o método é o mesmo: alinhe as bases e trabalhe nos numeradores com segurança, conferindo se o resultado aceita simplificação e, quando fizer sentido, convertendo para número misto para comunicar melhor o valor obtido.