Um prisma hexagonal é um sólido geométrico com uma base em forma de hexágono e faces laterais que formam paralelogramos. Para determinar quantas arestas possui um prisma hexagonal, devemos considerar as arestas da base (6 arestas) e as arestas das faces laterais (18 arestas, já que cada face lateral possui 3 arestas). Portanto, um prisma hexagonal possui um total de 24 arestas.
Número de arestas em um prisma hexagonal: qual a quantidade total?
Um prisma hexagonal é uma figura geométrica tridimensional que possui 6 faces em forma de hexágonos e 12 arestas. Para determinar o número total de arestas em um prisma hexagonal, precisamos levar em consideração que cada uma das 6 faces está conectada a outras 2 faces através de uma aresta compartilhada.
Isso significa que cada aresta do hexágono superior está conectada a uma aresta do hexágono inferior, totalizando 6 arestas que estão compartilhadas entre os dois hexágonos. Além disso, cada uma das 6 faces laterais está conectada a uma face superior e a uma face inferior, contribuindo com mais 6 arestas.
Portanto, somando as 6 arestas compartilhadas entre os hexágonos e as 6 arestas das faces laterais, obtemos um total de 12 arestas em um prisma hexagonal.
Quantidade de arestas em um prisma: descubra o número de lados!
Um prisma é um poliedro com duas faces congruentes e paralelas chamadas de bases, e faces laterais que são paralelogramos. Para descobrir a quantidade de arestas em um prisma, é importante primeiro identificar o número de lados da base do prisma.
No caso de um prisma hexagonal, a base possui seis lados. Cada lado da base é uma aresta, então um prisma hexagonal possui seis arestas na base. Além disso, um prisma possui uma aresta em cada vértice da base que se conecta à base oposta, ou seja, seis arestas adicionais.
Portanto, a quantidade total de arestas em um prisma hexagonal é a soma das arestas da base e das arestas que conectam os vértices das bases opostas. Assim, um prisma hexagonal possui um total de doze arestas.
Quantidade de faces, arestas e vértices em um hexágono.
Um hexágono é uma figura geométrica com seis lados. Ele possui seis faces, doze arestas e oito vértices. Cada face do hexágono é um polígono com seis lados, enquanto cada vértice é um ponto onde duas arestas se encontram. As arestas são as linhas que conectam os vértices do hexágono.
Quantas arestas possui um prisma hexagonal?
Um prisma hexagonal é um sólido geométrico que possui duas bases em forma de hexágonos e seis faces laterais que são retângulos. Portanto, um prisma hexagonal possui doze arestas. As arestas do prisma são as linhas que formam as arestas das bases e as arestas laterais que conectam as bases.
Principais características e definição de um prisma hexagonal regular.
Um prisma hexagonal regular é um sólido geométrico composto por duas bases hexagonais paralelas e seis faces laterais retangulares. As bases e as faces laterais são perpendiculares entre si, e as faces laterais são todas congruentes.
As bases do prisma hexagonal regular são hexágonos regulares, ou seja, todos os lados e ângulos são iguais. Isso garante que as faces laterais do prisma sejam retângulos com lados opostos iguais e ângulos retos.
Uma característica importante do prisma hexagonal regular é que todas as suas arestas têm o mesmo comprimento. Isso significa que as arestas das bases e as arestas das faces laterais têm medidas iguais.
Para determinar quantas arestas um prisma hexagonal regular possui, podemos observar que cada base hexagonal tem 6 arestas e cada face lateral retangular tem 4 arestas. Portanto, um prisma hexagonal regular tem 18 arestas no total: 6 arestas nas bases e 12 arestas nas faces laterais.
Quantas arestas possui um prisma hexagonal?
Para saber quantas arestas um prisma hexagonal precisa conhecer o significado de “aresta”, “prisma” e “hexagonal”. Os dois primeiros conceitos são definições gerais, e o terceiro tem a ver com a forma da figura geométrica.
Quando se fala em hexagonal, está sendo mencionado um hexágono (polígono). O prefixo “hexa” indica que o polígono tem seis lados.

Uma aresta é uma aresta de um objeto. Geometricamente, é uma linha que conecta dois vértices consecutivos de uma figura geométrica.
Um prisma é uma figura geométrica limitada por duas bases que são polígonos paralelos e iguais e suas faces laterais são paralelogramos.
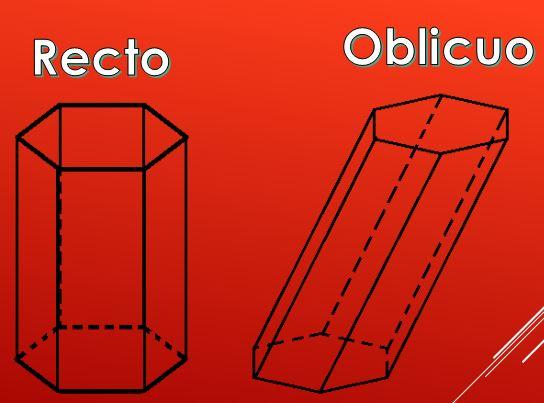
Na imagem a seguir, pode ser visto que as faces laterais de um prisma hexagonal podem ser retângulos, mas também podem ser paralelogramos.
De acordo com o tipo de paralelogramos, os prêmios podem ser classificados em dois tipos: retos e oblíquos.
Como contar as arestas de um prisma hexagonal?
O número de arestas que um prisma hexagonal terá não será alterado se for um prisma reto ou oblíquo.Além disso, o número de arestas também não depende do comprimento dos lados.
Contar as arestas de um prisma hexagonal pode ser feito de várias maneiras. Duas maneiras são descritas abaixo:
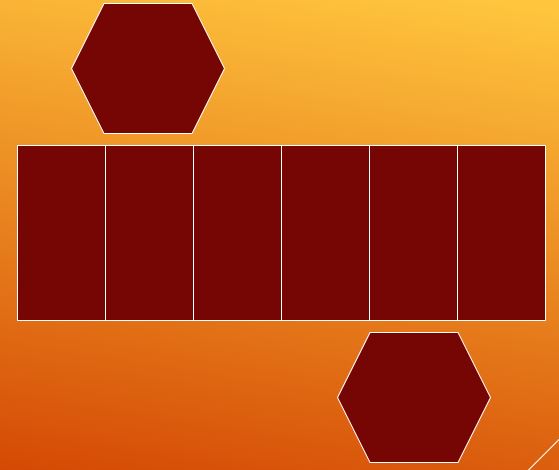
1- Decompor o prisma
Uma maneira de contar as arestas é quebrar o prisma hexagonal em suas duas bases e faces laterais. Desta forma, dois hexágonos e um paralelogramo com cinco linhas interiores são obtidos.
Cada hexágono tem seis arestas, portanto, o prisma terá mais de 12 arestas.
À primeira vista, pensa-se que o paralelogramo contém nove arestas (sete verticais e duas horizontais). Mas é conveniente parar para analisar este caso.
Quando o paralelogramo é dobrado para formar o prisma, pode-se ver que a primeira linha à esquerda se unirá à última linha à direita, com a qual ambas as linhas representam uma única aresta.
Mas e as duas linhas horizontais?
Quando todas as peças forem reunidas novamente, as linhas horizontais serão unidas, cada uma com as seis arestas de cada hexágono. Por esse motivo, contá-los separadamente seria um erro.
Portanto, o paralelogramo contém seis arestas do prisma que, juntamente com as 12 arestas contadas no início, fornecem um total de 18 arestas.
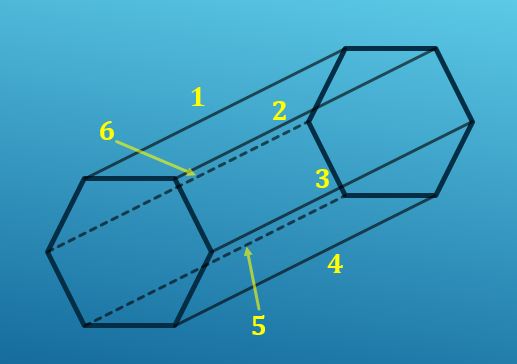
2.- Projetando cada aresta
Outra maneira, muito mais simples de contar as arestas, é usar o fato de que as bases dos prismas hexagonais são hexágonos, de modo que cada base tem seis arestas.
Por outro lado, de cada vértice de um hexágono, uma única aresta é projetada no vértice correspondente do outro hexágono; isto é, existem seis arestas que unem uma base à outra.
Ao adicionar todas as arestas, você obtém um total de 18 arestas.
Conclusão
Pode-se mostrar que o número de arestas de um prisma é igual a três vezes o número de arestas que o polígono que o forma.
Portanto, um prisma pentagonal terá 3 * 5 = 15 arestas, um prisma heptagonal terá 3 * 7 = 21 arestas e, portanto, pode ser aplicado a qualquer prisma.
Referências
- Billstein, R., Libeskind, S., & Lott, JW (2013).Matemática: uma abordagem de resolução de problemas para professores do ensino fundamental. Editores López Mateos.
- Fregoso, RS, & Carrera, SA (2005).Matemática 3. Progreso Editorial.
- Gallardo, G. e Pilar, PM (2005).Matemática 6. Progreso Editorial.
- Gutiérrez, CT, & Cisneros, MP (2005).Curso de Matemática 3º. Editorial Progreso.
- Kinsey, L. & Moore, TE (2006).Simetria, forma e espaço: uma introdução à matemática através da geometria (ilustrado, reimpresso ed.). Springer Science & Business Media.
- Mitchell, C. (1999).Projetos deslumbrantes da linha matemática (ed. Ilustrado). Scholastic Inc.
- R., MP (2005).Eu desenho em sexto. Editorial Progreso.