As derivadas algébricas são um ramo da matemática que estuda a taxa de variação de funções algébricas. Elas são essenciais para a análise de problemas relacionados a otimização, crescimento e taxas de mudança em diversas áreas da ciência e engenharia. A derivada de uma função algébrica é a inclinação da reta tangente à curva da função em um determinado ponto. Ela pode ser calculada utilizando regras de derivação específicas para cada tipo de função, como polinômios, exponenciais, logaritmos, entre outros.
Um exemplo simples de derivada algébrica é a função f(x) = x^2. Para calcular a derivada desta função, utilizamos a regra de derivação para potências, que diz que a derivada de x^n é n*x^(n-1). Portanto, a derivada de f(x) = x^2 é f'(x) = 2x. Isso significa que a inclinação da reta tangente à curva da função f(x) = x^2 em qualquer ponto x é igual a 2x.
Conheça os diversos tipos de derivadas e suas aplicações na matemática e física.
Derivadas são um dos conceitos fundamentais da matemática, utilizadas para descrever a taxa de variação de uma função em um determinado ponto. Existem diversos tipos de derivadas, cada uma com suas próprias características e aplicações em diferentes áreas, como a álgebra e a física.
As derivadas algébricas são aquelas que envolvem funções polinomiais e racionais, ou seja, funções compostas por operações matemáticas básicas como adição, subtração, multiplicação e divisão. Para calcular a derivada de uma função algébrica, utilizamos as regras básicas de diferenciação, como a regra do produto e a regra do quociente.
Por exemplo, considere a função f(x) = 3x^2 + 2x – 5. Para encontrar a derivada desta função, aplicamos a regra da potência para cada termo da função, resultando em f'(x) = 6x + 2. Assim, a derivada da função f(x) é f'(x) = 6x + 2.
As derivadas algébricas são amplamente utilizadas em diversas áreas da matemática e da física, como no cálculo de velocidades e acelerações em movimentos, na determinação de pontos críticos de funções, e na análise de comportamentos de sistemas dinâmicos. Portanto, compreender e dominar o cálculo de derivadas algébricas é essencial para o estudo e aplicação da matemática e da física.
Descubra o resultado da equação matemática 2B = -5EC ao calcular a expressão algébrica.
Para resolver a equação matemática 2B = -5EC, primeiro devemos isolar a variável B. Para isso, dividimos ambos os lados da equação por 2, obtendo assim B = -5/2EC. Agora, podemos substituir a expressão encontrada para B em qualquer outra equação ou expressão que envolva essa variável.
As derivadas algébricas são utilizadas para calcular a taxa de variação de uma função em relação a uma variável. Elas são fundamentais em cálculos de otimização, física, economia e muitas outras áreas da matemática e ciências aplicadas.
Um exemplo simples de derivada algébrica é a função f(x) = 3x^2. Para encontrar a derivada dessa função em relação a x, utilizamos a regra de potência, multiplicando o expoente pelo coeficiente e subtraindo 1 do expoente. Assim, a derivada de f(x) é f'(x) = 6x.
Como realizar o cálculo de uma expressão matemática utilizando álgebra?
Para realizar o cálculo de uma expressão matemática utilizando álgebra, é importante seguir alguns passos fundamentais. Primeiramente, é necessário identificar as variáveis presentes na expressão e atribuir a elas valores específicos. Em seguida, substituímos esses valores na expressão e simplificamos a equação utilizando as regras da álgebra, como a distributiva e a associativa.
Um exemplo simples seria a expressão 2x + 3y, onde x = 2 e y = 4. Substituímos os valores de x e y na expressão, resultando em 2*2 + 3*4. Após realizar as operações, obtemos o resultado final de 4 + 12 = 16.
Derivadas algébricas
As derivadas algébricas são utilizadas para calcular a taxa de variação de uma função em um determinado ponto. Para calcular a derivada de uma expressão algébrica, utilizamos as regras básicas de derivação, como a regra do produto, a regra da cadeia e a regra do quociente.
Um exemplo de cálculo de derivada algébrica seria a função f(x) = 2x^2 + 3x + 1. Para encontrar a derivada dessa função em relação a x, aplicamos as regras de derivação, resultando em f'(x) = 4x + 3.
Descubra a derivada da função f(x) = 2x² de forma simples e rápida.
Para descobrir a derivada da função (f(x) = 2x^2), podemos utilizar a regra da potência. Neste caso, a derivada de (x^n) é (nx^{n-1}). Portanto, a derivada de (2x^2) será (2 times 2x^{2-1} = 4x). Assim, a derivada da função (f(x) = 2x^2) é (f'(x) = 4x).
Para exemplificar, vamos encontrar a derivada da função (g(x) = 3x^3). Seguindo a mesma regra da potência, temos que a derivada de (3x^3) será (3 times 3x^{3-1} = 9x^2). Portanto, a derivada da função (g(x) = 3x^3) é (g'(x) = 9x^2).
Derivadas algébricas (com exemplos)
Os derivados algébricas consistem no estudo do derivado, no caso de funções algébricas. A origem da noção de derivada remonta à Grécia Antiga. O desenvolvimento dessa noção foi motivado pela necessidade de resolver dois problemas importantes, um em física e outro em matemática.
Na física, a derivada resolve o problema de determinar a velocidade instantânea de um objeto em movimento. Em matemática, permite encontrar a linha tangente a uma curva em um determinado ponto.

Embora haja realmente muitos outros problemas resolvidos usando a derivada, bem como suas generalizações, resultados que vieram mais tarde à introdução de seu conceito.
Os pioneiros do cálculo diferencial são Newton e Leibniz.Antes de dar a definição formal, desenvolveremos a idéia por trás dela, do ponto de vista matemático e físico.
A derivada como inclinação da linha tangente a uma curva
Suponha que o gráfico de uma função y = f (x) seja um gráfico contínuo (sem picos, vértices ou separações) e permita que A = (a, f (a)) seja um ponto fixo nela. Queremos encontrar a equação da reta tangente ao gráfico da função f no ponto A.
Vamos pegar qualquer outro ponto P = (x, f (x)) do gráfico, próximo ao ponto A, e desenhar a linha secante que passa por A e P. Uma linha secante é uma linha que corta o gráfico de uma curva em uma ou mais pontos.

Para obter a linha tangente que queremos, precisamos apenas calcular a inclinação porque já temos um ponto na linha: ponto A.
Se movermos o ponto P pelo gráfico e o aproximarmos cada vez mais do ponto A, a linha secante mencionada acima se aproximará da linha tangente que você deseja encontrar. Tomando o limite quando “P tende a A”, ambas as linhas coincidem, portanto, suas inclinações também.
A inclinação da linha secante é dada por

Dizer que P se aproxima de A é equivalente a dizer que “x” se aproxima de “a”. Assim, a inclinação da reta tangente ao gráfico de f no ponto A será igual a:

A expressão anterior é denotada por f ‘(a) e é definida como a derivada de uma função f no ponto “a”. Vimos que analiticamente, a derivada de uma função em um ponto é um limite, mas geometricamente, é a inclinação da linha tangente ao gráfico da função no ponto.
Agora veremos essa noção do ponto de vista da física. Vamos chegar à mesma expressão do limite anterior, embora por um caminho diferente, obtendo assim a unanimidade da definição.
A derivada como velocidade instantânea de um objeto em movimento
Vejamos um breve exemplo do que significa velocidade instantânea. Quando se diz, por exemplo, que um carro para chegar a um destino o fazia com uma velocidade de 100 km por hora, o que significa é que em uma hora ele percorreu 100 km.
Isso não significa necessariamente que, durante todo o tempo em que o carro estava sempre a 100 km, o velocímetro do carro poderia em alguns momentos marcar menos ou mais. Se você precisava parar em um semáforo, a velocidade naquele momento era 0 km. No entanto, após uma hora, o percurso foi de 100 km.
Isso é conhecido como velocidade média e é dado pela razão da distância percorrida entre o tempo decorrido, como acabamos de ver. A velocidade instantânea, por outro lado, é a que marca a agulha do velocímetro de um carro em um dado momento (tempo).
Vejamos isso agora de uma maneira mais geral. Suponha que um objeto se mova ao longo de uma linha e que esse deslocamento seja representado pela equação s = f (t), em que a variável t mede o tempo e a variável s o deslocamento, levando em consideração seu início em o momento t = 0, momento em que também é zero, ou seja, f (0) = 0.
Esta função f (t) é conhecida como função de posição.
Uma expressão é procurada para a velocidade instantânea do objeto em um instante fixo “a”. A essa velocidade, iremos denotá-lo por V (a).
Seja t um instante próximo do instante “a”. No intervalo de tempo entre “a” e “t”, a mudança na posição do objeto é dada por f (t) -f (a).
A velocidade média neste intervalo de tempo é:

Qual é uma aproximação da velocidade instantânea V (a). Essa abordagem será melhor à medida que você se aproxima de “a”. Portanto,

Observe que essa expressão é igual à obtida no caso anterior, mas de uma perspectiva diferente. Isso é conhecido como derivada de uma função f no ponto “a” e é denotada por f ‘(a), como afirmado acima.
Observe que, ao fazer a alteração h = xa, é que quando “x” tende a “a”, “h” tende a 0 e o limite anterior é transformado (equivalentemente) em:

Ambas as expressões são equivalentes, mas às vezes é melhor usar uma em vez da outra, dependendo do caso.
A derivada de uma função f é então definida mais geralmente em qualquer ponto “x” pertencente ao seu domínio como
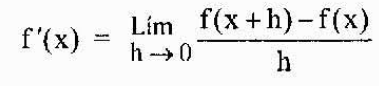
A notação mais comum para representar a derivada de uma função y = f (x) é a que acabamos de ver (f ‘o y’). No entanto, outra notação amplamente usada é a notação de Leibniz, representada como uma das seguintes expressões:
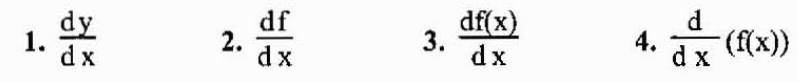
Como a derivada é essencialmente um limite, ela pode ou não existir, uma vez que os limites nem sempre existem. Se existir, diz-se que a função em questão é diferenciável no ponto especificado.
Função algébrica
Uma função algébrica é uma combinação de polinômios por meio de adição, subtração, produtos, quocientes, potências e radicais.
Um polinômio é uma expressão da forma
P n = a n x n + a n-1 x n-1 + a n-2 x n-2 +… + a 2 x 2 + a 1 x + a 0
Onde n é um número natural e todos ai , com i = 0,1, …, n, são números racionais e n ≠ 0. Nesse caso, diz-se que o grau desse polinômio é n.
A seguir, exemplos de funções algébricas:

Funções exponenciais, logarítmicas e trigonométricas não estão incluídas aqui. As regras de derivação que veremos abaixo são válidas para funções em geral, mas vamos nos restringir e aplicá-las no caso de funções algébricas.
Regras de Referência
Derivado de uma constante
Ele afirma que a derivada de uma constante é zero. Ou seja, se f (x) = c, então f ‘(x) = 0. Por exemplo, a derivada da função constante 2 é igual a 0.
Derivado de um poder
Se f (x) = x n , então f ‘(x) = nx n-1 . Por exemplo, a derivada de x 3 é 3x 2 . Como conseqüência disso, obtém-se que a derivada da função de identidade f (x) = x é f ‘(x) = 1x 1-1 = x 0 = 1.
Outro exemplo é o seguinte: seja f (x) = 1 / x 2 , então f (x) = x -2 ef ‘(x) = – 2x -2-1 = -2x -3 .
Essa propriedade também possui raízes válidas, uma vez que as raízes são poderes racionais e o acima também pode ser aplicado nesse caso. Por exemplo, a derivada de uma raiz quadrada é dada por

Derivado de uma soma e uma subtração
Se f e g são funções diferenciáveis em x, então a soma f + g também é diferente e é verdade que (f + g) ‘(x) = f’ (x) + g ‘(x).
Da mesma forma, você deve (fg) ‘(x) = f’ (x) -g ‘(x). Em outras palavras, a derivada de uma soma (subtração) é a soma (ou subtração) das derivadas.
Exemplo
Se h (x) = x 2 + x-1, então
h ‘(x) = (x 2 ) + (x)’ – (1) ‘= 2x + 1-0 = 2x + 1.
Derivada do produto
Se f e g são funções diferenciáveis em x, então o produto fg também é diferenciável em x e é cumprido que
(fg) ‘(x) = f’ (x) g (x) + f (x) g ‘(x).
Como conseqüência, se c é uma constante ef é uma função diferenciável em x, então cf também é diferenciável em xy (cf) ‘(x) = cf’ (X).
Exemplo
Se f (x) = 3x (x 2 +1), então
f ‘(x) = (3x)’ (x 2 +1) + (3x) (x 2 +1) ‘= 3 (x)’ (x 2 +1) + 3x [(x 2 ) ‘+ (1 ) ‘]
= 3 (1) (x 2 +1) + 3x [(2x 2-1 ) +0] = 3 (x 2 +1) + 3x (2x) = 3x 2 + 3 + 6x 2
= 9x 2 +3.
Derivado de um quociente
Se f e g são diferenciáveis em x e g (x) ≠ 0, então f / g também é diferenciável em x, e é cumprido que

Exemplo: se h (x) = x 3 / (x 2 -5x), então
h ‘(x) = [(x 3 )’ (x 5 -5x) – (x 3 ) (x 5 -5x) ‘] / (x 5 -5x) 2 = [(3x 2 ) (x 5 -5x ) – (x 3 ) (5x 4 -5)] / (x 5 -5x) 2 .
Regra da cadeia
Esta regra permite derivar a composição de funções. Ele afirma o seguinte: se y = f (u) é diferenciável em u, yu = g (x) é diferenciável em x, então a função composta f (g (x)) é diferenciável em x, e é verdade que [f ( g (x))] ‘= f’ (g (x)) g ‘(x).
Ou seja, a derivada de uma função composta é o produto da derivada da função externa (derivada externa) pela derivada da função interna (derivada interna).
Exemplo
Se f (x) = (x 4 -2x) 3 , então
f ‘(x) = 3 (x 4 -2x) 2 (x 4 -2x)’ = 3 (x 4 -2x) 2 (4x 3 -2).
Também existem resultados para calcular a derivada do inverso de uma função, bem como a generalização para derivadas de ordem superior. As aplicações são extensas. Entre eles, destacam suas utilidades em problemas de otimização e funções máxima e mínima.
Referências
- Alarcon, S., González, M. e Quintana, H. (2008). Cálculo diferencial. ITM
- Cabrera, VM (1997). Cálculo 4000. Progreso Editorial.
- Castaño, HF (2005). Matemática antes do cálculo. Universidade de Medellín.
- Eduardo, NA (2003). Introdução ao cálculo. Edições de limite.
- Fuentes, A. (2016). MATEMÁTICA BÁSICA. Uma introdução ao cálculo. Lulu.com
- Purcell, EJ, Rigdon, SE & Varberg, DE (2007). Cálculo Pearson Education.
- Saenz, J. (2005). Cálculo Diferencial (Segunda ed.). Barquisimeto: Hipotenusa.
- Thomas, GB e Weir, MD (2006). Cálculo: várias variáveis. Pearson Education.