A divisão sintética é um método utilizado para dividir polinômios de forma rápida e eficiente, principalmente quando o divisor é do tipo (x – a). Este método é muito útil para simplificar cálculos e resolver equações polinomiais de maneira mais prática. Neste livro, apresentaremos os fundamentos da divisão sintética, passo a passo, e resolveremos diversos exercícios para que o leitor possa compreender e aplicar esse método de forma eficaz.
Entenda o funcionamento do método Briot Ruffini para divisão de polinômios de forma simplificada.
O método Briot Ruffini é uma técnica utilizada para dividir polinômios de forma mais simples e rápida. Ele é uma forma de divisão sintética que facilita o processo de encontrar o quociente e o resto da divisão.
Para utilizar o método Briot Ruffini, é necessário organizar os coeficientes do polinômio de forma correta, garantindo que não haja lacunas entre os termos. Em seguida, escolhemos um número que será o divisor da divisão e realizamos as operações de forma sistemática.
Para realizar a divisão sintética com o método Briot Ruffini, seguimos os passos: dividimos o primeiro termo do polinômio original pelo divisor, multiplicamos o resultado pelo divisor e subtraímos do segundo termo do polinômio original, repetindo o processo até chegar ao último termo.
Assim, obtemos o quociente da divisão na última linha da tabela, com os coeficientes do polinômio resultante. O último valor da tabela corresponde ao resto da divisão, se for diferente de zero indica que não houve divisão exata.
O método Briot Ruffini é uma ferramenta muito útil para resolver divisões de polinômios de forma mais prática e eficiente. Com a prática e o entendimento correto do método, é possível realizar divisões de polinômios com mais facilidade e rapidez.
Passo a passo para resolver polinômios de forma simples e eficiente.
Para resolver polinômios de forma simples e eficiente, podemos utilizar a Divisão Sintética. Esse método é muito útil para dividir um polinômio por um binômio da forma (x – a). Vamos ver como fazer isso passo a passo:
Passo 1: Escreva o polinômio na forma padrão, com todos os termos presentes, mesmo que alguns tenham coeficientes zero.
Passo 2: Escreva o binômio divisor na forma (x – a), onde “a” é o número que está do lado oposto do sinal de menos. Se o binômio divisor for (x + a), mude o sinal de “a” para negativo.
Passo 3: Coloque o valor de “a” fora do polinômio na divisão sintética e faça uma linha vertical para separar os coeficientes. Se faltar algum termo no polinômio, complete com zeros.
Passo 4: Escreva os coeficientes do polinômio dentro da linha vertical, na ordem decrescente de expoentes de x. Se algum termo estiver faltando, coloque zero no lugar.
Passo 5: Realize a divisão sintética, trazendo o primeiro coeficiente para baixo, multiplicando pelo valor de “a” e somando com o próximo coeficiente. Repita o processo até chegar ao último coeficiente.
Passo 6: Os valores obtidos após a divisão sintética correspondem aos coeficientes do quociente da divisão. Escreva o quociente resultante e lembre-se de que o último valor é o resto da divisão.
Agora que você sabe como resolver polinômios utilizando a divisão sintética, pratique com alguns exercícios para consolidar o conhecimento. Com o tempo e a prática, você se tornará mais ágil e eficiente nesse método de resolução.
Passo a passo para realizar a divisão de polinômios de forma simples e eficaz.
A divisão de polinômios pode ser feita de forma simples e eficaz utilizando o método da divisão sintética. Este método é muito útil para dividir polinômios de grau mais alto, economizando tempo e facilitando o cálculo. A seguir, vamos apresentar um passo a passo para realizar a divisão de polinômios utilizando a divisão sintética.
Passo 1: Organize os polinômios
Antes de iniciar a divisão, certifique-se de que os polinômios estão organizados de forma correta, com os termos de cada polinômio alinhados em ordem decrescente de grau. Por exemplo, se você deseja dividir o polinômio (3x^3 + 2x^2 – 5x + 1) por (x – 2), certifique-se de que os termos estão organizados corretamente.
Passo 2: Identifique os coeficientes
Identifique os coeficientes do polinômio que está sendo dividido e do divisor. No exemplo acima, os coeficientes seriam 3, 2, -5 e 1 para o dividendo e 1 e -2 para o divisor.
Passo 3: Realize a divisão sintética
Utilize a tabela da divisão sintética para realizar a divisão dos coeficientes. Coloque o coeficiente do dividendo na primeira linha da tabela e o coeficiente do divisor na segunda linha. Em seguida, faça os cálculos necessários para encontrar o quociente e o resto da divisão.
Passo 4: Verifique o resultado
Após realizar os cálculos, verifique se o resultado obtido está correto. O quociente da divisão será o coeficiente dos termos do quociente, enquanto o resto será o último valor da tabela da divisão sintética.
Seguindo esses passos simples, você poderá realizar a divisão de polinômios de forma fácil e eficaz, utilizando o método da divisão sintética. Pratique com exercícios resolvidos para aprimorar suas habilidades e se tornar mais confiante na resolução de problemas de divisão de polinômios.
Aprenda a realizar divisão de um polinômio por um binômio passo a passo.
A Divisão Sintética é um método utilizado para realizar a divisão de um polinômio por um binômio de forma mais simplificada. Neste artigo, vamos explicar passo a passo como realizar esse processo de forma eficiente.
Para começar, vamos considerar um polinômio P(x) dividido por um binômio do tipo (x-a), onde “a” é um número real. O objetivo é encontrar o quociente Q(x) e o resto R(x) da divisão.
O primeiro passo é organizar os coeficientes do polinômio P(x) de forma decrescente, ou seja, do maior grau para o menor grau. Se algum termo do polinômio estiver faltando, é importante preencher com um coeficiente zero.
Em seguida, escrevemos o valor de “a” do binômio (x-a) no canto direito e os coeficientes do polinômio na linha de baixo.
Agora, realizamos a divisão sintética, que consiste em multiplicar o valor de “a” pelo coeficiente do termo de maior grau do polinômio, somar com o próximo coeficiente, multiplicar novamente por “a” e assim por diante. Os resultados obtidos são os coeficientes do quociente Q(x) e o último valor é o resto R(x).
Por fim, o quociente Q(x) representa o resultado da divisão e o resto R(x) é o valor que não foi possível dividir pelo binômio.
Com esse método, é possível realizar a divisão de um polinômio por um binômio de forma mais rápida e prática. Pratique com exercícios resolvidos para aprimorar suas habilidades em divisão sintética.
Divisão Sintética: Método e Exercícios Resolvidos
A divisão sintético é uma forma simples de dividir um polinómio P (x) qualquer um da forma d (x) = x – c. É uma ferramenta muito útil, pois, além de nos permitir dividir polinômios, também nos permite avaliar um polinômio P (x) em qualquer número c, o que, por sua vez, indica precisamente se o número é zero ou não do polinômio.
Graças ao o algoritmo da divisão, nós sabemos que se nós temos dois polinômios P (x) e d (x) não é constante, não são polinômios q (x) e r (x) única tal que sustenta que P (x) = q (x ) d (x) + r (x), em que r (x) é zero ou tem um grau menor que q (x). Esses polinômios são conhecidos como quociente e resíduo ou restante, respectivamente.

Nas ocasiões em que o polinômio d (x) tem a forma x- c, a divisão sintética nos fornece um caminho curto para descobrir quem são q (x) er (x).
Método de divisão sintética
Seja P (x) = a n x n + a n-1 x n-1 + … + a 1 x + a 0 seja o polinômio que queremos dividir ed (x) = xc o divisor. Para dividir pelo método de divisão sintética, procedemos da seguinte forma:
1- Escrevemos os coeficientes de P (x) na primeira linha. Se qualquer potência de X não aparecer, colocamos zero como seu coeficiente.

2- Na segunda linha, à esquerda de um n, coloque c e desenhe linhas divisórias, conforme mostrado na figura a seguir:

3- Abaixamos o coeficiente inicial para a terceira linha.

Nesta expressão b n-1 = a n
4- Multiplicamos c pelo coeficiente inicial b n-1 e o resultado é escrito na segunda linha, mas uma coluna à direita.
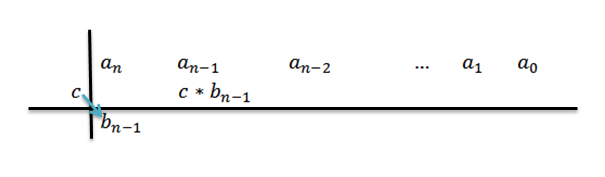
5- Adicione a coluna onde escrevemos o resultado anterior e coloque o resultado abaixo dessa soma; isto é, na mesma coluna, terceira linha.
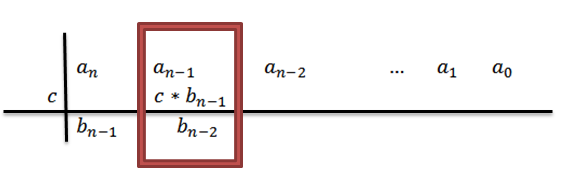
Ao adicionar, temos como resultado n-1 + c * b n-1 , que por conveniência chamaremos de b n-2
6- Multiplique c pelo resultado anterior e escreva o resultado à sua direita na segunda linha.
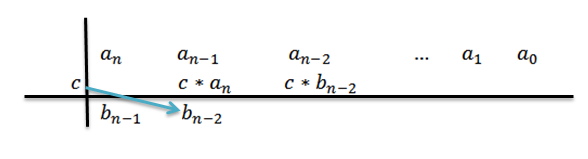
7- Repita as etapas 5 e 6 até atingir o coeficiente em 0 .

8- Nós escrevemos a resposta; isto é, o quociente e o resíduo. Como estamos dividindo um polinômio de grau n por um polinômio de grau 1, temos que o quociente seria de grau n-1.
Os coeficientes do polinômio quociente serão os números na terceira linha, exceto o último, que será o polinômio residual ou o restante da divisão.
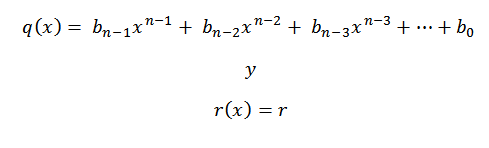
Exercícios resolvidos
Exemplo 1
Execute a seguinte divisão pelo método de divisão sintética:
(x 5 + 3x 4 -7x 3 + 2x 2 -8x + 1): (x + 1).
Solução
Primeiro, escrevemos os coeficientes de dividendos da seguinte forma:
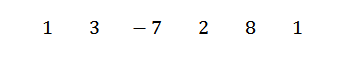
Em seguida, escrevemos c no lado esquerdo, na segunda linha, junto com as linhas divisórias. Neste exemplo c = -1.
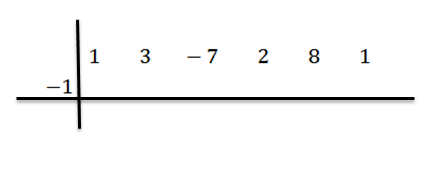
Reduzimos o coeficiente inicial (neste caso, b n-1 = 1) e multiplicamos por -1:

Escrevemos seu resultado à direita na segunda linha, como mostrado abaixo:
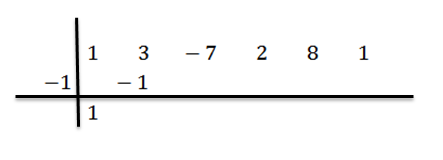
Nós adicionamos os números na segunda coluna:

Multiplicamos 2 por -1 e escrevemos o resultado na terceira coluna, segunda linha:

Nós adicionamos na terceira coluna:
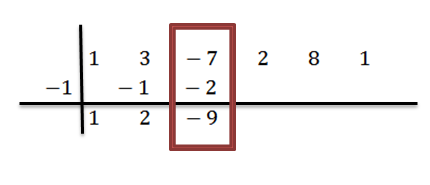
Procuramos analogamente até chegarmos à última coluna:

Portanto, temos que o último número obtido é o restante da divisão e os números restantes são os coeficientes do polinômio do quociente. Isso está escrito da seguinte maneira:

Se quisermos verificar se o resultado está correto, verifique se a seguinte equação foi atendida:
P (x) = q (x) * d (x) + r (x)
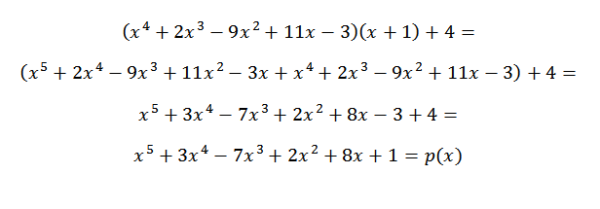
Assim, podemos verificar se o resultado obtido está correto.
Exemplo 2
Execute a seguinte divisão de polinômios pelo método de divisão sintética
(7x 3 -x + 2): (x + 2)
Solução
Nesse caso, temos que o termo x 2 não aparece, então escreveremos em 0 como seu coeficiente. Assim, o polinômio seria como 7x 3 + 0x 2 -x + 2.
Nós escrevemos seus coeficientes em uma linha, isto é:

Escrevemos o valor de C = -2 no lado esquerdo na segunda linha e desenhamos as linhas divisórias.

Reduzimos o coeficiente inicial b n-1 = 7 e o multiplicamos por -2, escrevendo seu resultado na segunda linha à direita.

Adicionamos e prosseguimos conforme explicado anteriormente, até chegarmos ao último termo:
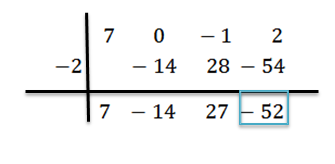
Nesse caso, o restante é r (x) = – 52 e o quociente obtido é q (x) = 7x 2 -14x + 27.
Exemplo 3
Outra maneira de usar a divisão sintética é a seguinte: suponha que tenhamos um polinômio P (x) de grau n e desejemos saber o que é valor ao avaliá-lo em x = c.
Pelo algoritmo de divisão, temos que escrever o polinômio P (x) da seguinte maneira:

Nessa expressão, q (x) er (x) são o quociente e o restante, respectivamente. Agora, se d (x) = x- c, ao avaliar c no polinômio, encontramos o seguinte:

É por isso que precisamos encontrar apenas ar (x), e podemos fazer isso graças à divisão sintética.
Por exemplo, temos o polinômio P (x) = x 7 -9x 6 + 19x 5 + 12x 4 -3x 3 + 19x 2 -37x-37 e queremos saber qual é o seu valor ao avaliar em x = 5. Para isso, executamos o Divisão entre P (x) ed (x) = x -5 pelo método da divisão sintética:

Após a conclusão das operações, sabemos que podemos escrever P (x) da seguinte maneira:
P (x) = (x 6 -4x 5 –x 4 + 7x 3 + 32x 2 + 179x + 858) * (x-5) + 4253
Portanto, ao avaliar, temos que:
P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (5-5) + 4253
P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (0) + 4253
P (5) = 0 + 4253 = 4253
Como podemos ver, é possível usar a divisão sintética para encontrar o valor de um polinômio ao avaliá-lo em c em vez de simplesmente substituir c por x.
Se tentássemos avaliar P (5) da maneira tradicional, precisaríamos realizar alguns cálculos que geralmente se tornam entediantes.
Exemplo 4
O algoritmo da divisão para polinômios também é realizado para polinômios com coeficientes complexos e, como conseqüência, temos que o método de divisão sintética também funciona para esses polinômios. A seguir, veremos um exemplo.
Usaremos o método de divisão sintética para mostrar que z = 1+ 2i é um zero do polinômio P (x) = x 3 + (1 + i) x 2 – (1 + 2i) x + (15 + 5i); isto é, o restante da divisão P (x) por d (x) = x – z é igual a zero.
Procedemos como antes: na primeira linha, escrevemos os coeficientes de P (x), depois, na segunda, escrevemos z e desenhamos as linhas divisórias.
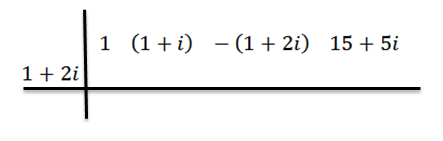
Executamos a divisão como antes; isto é:
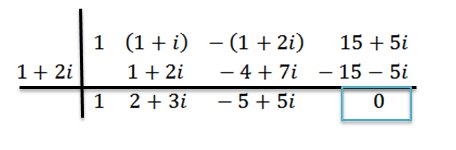
Podemos observar que o resíduo é zero; portanto, concluímos que, z = 1+ 2i é um zero de P (x).
Referências
- Baldor Aurelio. Álgebra . Grupo Editorial Patria.
- Demana, espera, Foley e Kennedy. Pré-cálculo: Gráfico, numérico, algébrico 7th Ed. Pearson Education.
- Flemming W & Varserg D. Álgebra e Trigonometria com Geometria Analítica. Prentice Hall
- Michael Sullivan Pré-cálculo 4ª Ed. Pearson Education.
- Vermelho. Armando ó . Álgebra 1 6a Ed. O Ateneu