A máquina de Carnot é um modelo ideal de um motor térmico que opera de forma reversível e eficiente, proposto pelo físico francês Sadi Carnot em 1824. Este modelo teórico serve como base para entender o funcionamento de motores reais e sistemas de refrigeração. Neste artigo, exploraremos as fórmulas matemáticas que regem o funcionamento da máquina de Carnot, como ela opera e suas aplicações práticas em diferentes contextos.
Fórmula do ciclo de Carnot: como calcular a eficiência de um motor térmico ideal.
A máquina de Carnot é um modelo teórico de um motor térmico ideal que opera segundo um ciclo reversível. A eficiência desse motor pode ser calculada usando a fórmula do ciclo de Carnot, que é dada pela expressão:
η = 1 – (Tc/Th)
Onde η representa a eficiência do motor, Tc é a temperatura da fonte fria e Th é a temperatura da fonte quente. Quanto mais próxima a temperatura da fonte quente estiver da temperatura absoluta zero, maior será a eficiência do motor.
A máquina de Carnot opera segundo quatro etapas: compressão isoterma, aquecimento isoterma, expansão isoterma e resfriamento isoterma. Durante essas etapas, o gás no interior do motor sofre variações de pressão e temperatura, resultando em trabalho realizado e troca de calor com as fontes quente e fria.
Apesar de ser um modelo teórico, a máquina de Carnot é importante para entender o funcionamento dos motores térmicos e para estabelecer limites teóricos de eficiência. Ela é amplamente utilizada em estudos de termodinâmica e em aplicações práticas na engenharia.
Entenda o funcionamento da máquina de Carnot e sua eficiência termodinâmica.
A máquina de Carnot é um dispositivo teórico ideal que opera de acordo com o ciclo termodinâmico de Carnot. Desenvolvido pelo físico francês Sadi Carnot em 1824, esse modelo é utilizado para estudar os princípios da termodinâmica e a eficiência das máquinas térmicas.
A máquina de Carnot é composta por duas fontes de calor – uma quente e uma fria – e por dois reservatórios de temperatura constante. O ciclo de Carnot consiste em quatro processos reversíveis: dois processos isotérmicos e dois processos adiabáticos.
A eficiência termodinâmica da máquina de Carnot é dada pela fórmula: ɛ = 1 – (Tc/Th), onde ɛ representa a eficiência, Tc é a temperatura da fonte fria e Th é a temperatura da fonte quente. Quanto mais próxima a temperatura da fonte quente estiver da temperatura da fonte fria, maior será a eficiência da máquina de Carnot.
A eficiência da máquina de Carnot é a máxima possível para qualquer máquina térmica operando entre as mesmas temperaturas. Isso significa que, em termos de eficiência, a máquina de Carnot é o padrão de excelência para comparação com outros dispositivos.
Embora a máquina de Carnot seja um modelo teórico e não possa ser construída na prática, ela é fundamental para o estudo da termodinâmica e para entender os limites da eficiência das máquinas térmicas. Seu funcionamento e sua eficiência termodinâmica são essenciais para o desenvolvimento de tecnologias mais eficientes e sustentáveis.
Conheça as fases do ciclo termodinâmico ideal de Carnot em 4 passos simples.
A máquina de Carnot é um dispositivo termodinâmico que opera de acordo com o ciclo termodinâmico ideal de Carnot. Este ciclo consiste em quatro fases, que são descritas a seguir:
1. Compressão isotérmica: Nesta fase, o gás é comprimido a uma temperatura constante, resultando em um aumento da pressão e da energia interna.
2. Aquecimento isovolumétrico: Durante esta etapa, o gás é aquecido a volume constante, o que resulta em um aumento da pressão e da temperatura.
3. Expansão isotérmica: Nesta fase, o gás se expande a uma temperatura constante, resultando em uma diminuição da pressão e da energia interna.
4. Resfriamento isovolumétrico: Durante esta etapa final, o gás é resfriado a volume constante, resultando em uma diminuição da pressão e da temperatura.
Essas quatro fases formam o ciclo termodinâmico ideal de Carnot, que é amplamente utilizado para analisar o desempenho de máquinas térmicas. É importante ressaltar que este ciclo é idealizado e serve como referência para comparar o desempenho de outras máquinas.
O que é o teorema de Carnot e qual sua importância na termodinâmica?
O teorema de Carnot é um princípio fundamental da termodinâmica que estabelece limites para a eficiência de qualquer máquina térmica. Criado pelo físico francês Sadi Carnot em 1824, este teorema é essencial para entender o funcionamento de sistemas que convertem calor em trabalho mecânico.
A importância do teorema de Carnot na termodinâmica reside no fato de que ele define a eficiência máxima teórica de um processo de conversão de calor em trabalho. Isso significa que qualquer máquina real nunca poderá atingir 100% de eficiência, de acordo com as leis da termodinâmica.
As máquinas de Carnot são sistemas teóricos que operam de acordo com o ciclo de Carnot, um processo reversível que consiste em duas transformações isotérmicas e duas transformações adiabáticas. Essas máquinas são utilizadas como referência para comparar a eficiência de outros sistemas reais.
Para calcular a eficiência de uma máquina de Carnot, utiliza-se a fórmula:
η = 1 – (Tc/Th)
Onde η representa a eficiência da máquina, Tc é a temperatura da fonte fria e Th é a temperatura da fonte quente. Quanto mais próximas forem as temperaturas das fontes de calor, menor será a eficiência da máquina.
Apesar de ser um conceito teórico, o teorema de Carnot tem aplicações práticas em diversas áreas, como na engenharia de motores de combustão interna, na geração de energia eólica e na refrigeração. Compreender os limites impostos por este teorema ajuda os engenheiros a projetar sistemas mais eficientes e sustentáveis.
Carnot Machine: Fórmulas, Como Funciona e Aplicações
A máquina Carnot é um modelo cíclico ideal no qual o calor é usado para fazer um trabalho. O sistema pode ser entendido como um pistão que viaja dentro de um cilindro comprimindo um gás. O ciclo realizado é o de Carnot, enunciado pelo pai da termodinâmica, o físico e engenheiro francês Nicolas Léonard Sadi Carnot.
Carnot enunciou este ciclo no início do século XIX. A máquina está sujeita a quatro variações de estado, alternando condições como temperatura e pressão constante, onde uma variação do volume é evidente ao comprimir e expandir o gás.
Fórmulas
Segundo Carnot, sujeitando a máquina ideal a variações de temperatura e pressão, é possível maximizar o rendimento obtido.
O ciclo de Carnot deve ser analisado separadamente em cada uma de suas quatro fases: expansão isotérmica, expansão adiabática, compressão isotérmica e compressão adiabática.

A seguir, serão detalhadas as fórmulas associadas a cada uma das fases do ciclo realizadas na máquina Carnot.
Expansão isotérmica (A → B)
As premissas dessa fase são as seguintes:
– Volume de gás: passa do volume mínimo para um volume médio.
– Temperatura da máquina: temperatura constante T1, alto valor (T1> T2).
– Pressão da máquina: desce de P1 a P2.
O processo isotérmico implica que a temperatura T1 não varia durante esta fase. A transferência de calor induz a expansão de gás, o que induz movimento no pistão e produz trabalho mecânico.
Ao expandir, o gás tem uma tendência a esfriar. No entanto, absorve o calor emitido pela fonte de temperatura e durante sua expansão mantém a temperatura constante.
Como a temperatura permanece constante durante esse processo, a energia interna do gás não muda e todo o calor absorvido pelo gás é efetivamente transformado em trabalho. Assim:

Por outro lado, no final desta fase do ciclo também é possível obter o valor da pressão usando a equação de gás ideal. Assim, você tem o seguinte:
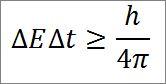
Nesta expressão:
P 2 : Pressão no final da fase.
V b : Volume no ponto b.
n: número de mols de gás.
R: Constante universal de gases ideais. R = 0,082 (atm * litro) / (moles * K).
T1: temperatura inicial absoluta, graus Kelvin.
Expansão adiabática (B → C)
Durante esta fase do processo, a expansão do gás ocorre sem a necessidade de troca de calor. Assim, as premissas estão detalhadas abaixo:
– Volume do gás: passa do volume médio para o volume máximo.
– Temperatura da máquina: cai de T1 para T2.
– Pressão da máquina: pressão constante P2.
O processo adiabático implica que a pressão P2 não varia durante esta fase. A temperatura diminui e o gás continua a se expandir até atingir seu volume máximo; isto é, o pistão atinge o topo.
Nesse caso, o trabalho realizado provém da energia interna do gás e seu valor é negativo porque a energia diminui durante esse processo.

Supondo que seja um gás ideal, é mantida a teoria de que as moléculas de gás possuem apenas energia cinética. De acordo com os princípios da termodinâmica, isso pode ser deduzido pela seguinte fórmula:
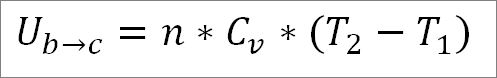
Nesta fórmula:
BU b → c : Variação interna de energia do gás ideal entre os pontos bec.
n: número de mols de gás.
Cv: capacidade de calor molar do gás.
T1: temperatura inicial absoluta, graus Kelvin.
T2: Temperatura final absoluta, graus Kelvin.
Compressão isotérmica (C → D)
Nesta fase, começa a compressão do gás; isto é, o pistão se move para dentro do cilindro, pelo qual o gás contrai seu volume.
As condições inerentes a esta fase do processo estão detalhadas abaixo:
– Volume do gás: varia do volume máximo a um volume intermediário.
– Temperatura da máquina: temperatura constante T2, valor reduzido (T2 <T1).
– Pressão da máquina: aumenta de P2 para P1.
Aqui a pressão sobre o gás aumenta, então começa a se comprimir. No entanto, a temperatura permanece constante e, portanto, a variação interna de energia do gás é zero.
Semelhante à expansão isotérmica, o trabalho realizado é igual ao calor do sistema. Assim:

Também é possível encontrar a pressão neste momento usando a equação de gás ideal.
Compressão adiabática (D → A)
Esta é a última fase do processo, na qual o sistema retorna às suas condições iniciais. Para isso, são consideradas as seguintes condições:
– Volume de gás: varia de um volume intermediário a um volume mínimo.
– Temperatura da máquina: aumenta de T2 para T1.
– Pressão da máquina: pressão constante P1.
A fonte de calor incorporada ao sistema na fase anterior é removida, para que o gás ideal aumente sua temperatura enquanto a pressão permanecer constante.
O gás retorna às condições iniciais de temperatura (T1) e seu volume (mínimo). Mais uma vez, o trabalho realizado vem da energia interna do gás, portanto, você deve:

Semelhante ao caso da expansão adiabática, é possível obter a variação da energia do gás através da seguinte expressão matemática:
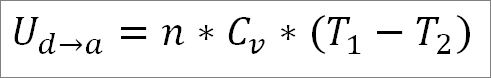
Como funciona a máquina Carnot?
A máquina Carnot funciona como um mecanismo no qual o desempenho é maximizado por processos isotérmicos e adiabáticos variados, alternando as fases de expansão e entendimento de um gás ideal.

O mecanismo pode ser entendido como um dispositivo ideal que executa um trabalho sujeito a variações de calor, dada a existência de duas fontes de temperatura.
No primeiro foco, o sistema é exposto a uma temperatura T1. É uma temperatura elevada que coloca o sistema sob estresse e produz expansão de gás.
Por sua vez, isso se traduz na execução de trabalhos mecânicos que permitem que o pistão se mova para fora do cilindro e cuja parada é possível apenas através de expansão adiabática.
Depois, vem o segundo foco, no qual o sistema é exposto a uma temperatura T2, menor que T1; isto é, o mecanismo está sujeito a refrigeração.
Isso induz a extração de calor e a trituração de gás, que atingem seu volume inicial após a compressão adiabática.
Aplicações
A máquina Carnot tem sido amplamente utilizada graças à sua contribuição na compreensão dos aspectos mais importantes da termodinâmica.
Esse modelo nos permite entender claramente as variações de gases ideais sujeitos a mudanças de temperatura e pressão, que é um método de referência ao projetar motores reais.
Referências
- Carnot Heat Engine Cycle e a 2ª Lei (sf). Recuperado de: nptel.ac.in
- Castellano, G. (2018). Máquina de Carnot Recuperado de: famaf.unc.edu.ar
- Ciclo de Carnot (sf). Havana, Cuba Recuperado de: ecured.cu
- O ciclo de Carnot (sf). Recuperado de: sc.ehu.es
- Fowler, M. (sf). Motores de calor: o ciclo de Carnot. Recuperado de: galileo.phys.virginia.edu
- Wikipedia, A Enciclopédia Livre (2016). Máquina de Carnot Recuperado de: en.wikipedia.org