Os choques inelásticos são colisões entre corpos em que parte da energia cinética é dissipada na forma de calor, som e deformações, resultando em uma diminuição da energia cinética total do sistema. Neste tipo de colisão, os corpos se fundem após o impacto e se movem juntos como um único corpo.
Neste artigo, abordaremos os choques inelásticos em uma dimensão, ou seja, quando os corpos envolvidos se movem ao longo da mesma reta. Além disso, apresentaremos exemplos comuns de choques inelásticos, como colisões entre veículos em estradas, bolas de bilhar em uma mesa de sinuca e objetos em movimento em uma linha de produção industrial.
Entender o conceito de choques inelásticos e seus efeitos é essencial para diversas áreas da física e engenharia, permitindo prever o comportamento de sistemas em colisão e otimizar projetos e processos que envolvam interações entre corpos em movimento.
Exemplos de colisão inelástica e sua definição de maneira simplificada.
Colisão inelástica ocorre quando dois corpos se chocam e permanecem unidos após o impacto, resultando em uma perda de energia cinética. Nesse tipo de colisão, parte da energia é transformada em outras formas de energia, como calor, som e deformação dos corpos.
Um exemplo comum de colisão inelástica é o choque entre dois carros em uma estrada. Quando os veículos se chocam, a energia cinética é dissipada na forma de calor e som, resultando em danos materiais e possíveis ferimentos aos ocupantes dos carros.
Outro exemplo é a colisão entre duas bolas de bilhar. Quando as bolas se chocam, parte da energia cinética é transformada em energia térmica e sonora, fazendo com que as bolas se movam juntas após o impacto.
Em resumo, nas colisões inelásticas, os corpos se chocam e permanecem unidos, resultando em uma perda de energia cinética que é transformada em outras formas de energia.
Definição de colisões em duas dimensões: conceito e aplicações práticas.
A colisão em duas dimensões ocorre quando dois objetos se chocam em um plano bidimensional, resultando em mudanças nas velocidades e direções de ambos os objetos. Esse fenômeno é comumente estudado na física, especialmente na mecânica, para entender como as forças atuam durante a interação entre os corpos.
As aplicações práticas das colisões em duas dimensões são vastas. Por exemplo, em simulações de acidentes de trânsito, é essencial compreender como os veículos se chocam e como as forças são distribuídas durante o impacto. Além disso, em jogos de computador e animações, a física das colisões em duas dimensões é usada para criar movimentos realistas e interações entre personagens e objetos.
Choques inelásticos: em uma dimensão e exemplos.
Um choque inelástico ocorre quando dois corpos se chocam e permanecem unidos após a colisão, resultando em perda de energia cinética. Nesse tipo de colisão, a quantidade de movimento é conservada, mas a energia não é.
Um exemplo clássico de choque inelástico em uma dimensão é o encontro entre uma bala de argila e um bloco de madeira em repouso. Quando a bala se choca com o bloco, os dois objetos se fundem e se movem juntos após a colisão, com uma velocidade menor do que a da bala inicialmente.
Outro exemplo comum de choque inelástico é o jogo de bilhar, onde as bolas colidem umas com as outras e perdem parte de sua energia cinética devido ao atrito e deformação durante a colisão.
Tipos de colisões: conheça os três principais impactos entre objetos em movimento.
Quando objetos em movimento se chocam, ocorrem diferentes tipos de colisões que podem ser classificadas de acordo com o resultado do impacto. Os três principais tipos de colisões são: elásticas, inelásticas e parcialmente elásticas.
As colisões elásticas são aquelas em que a energia cinética total do sistema é conservada. Isso significa que, após a colisão, os objetos continuam em movimento, sem perda de energia. Um exemplo comum de colisão elástica é o impacto entre duas bolas de bilhar.
Já as colisões inelásticas são aquelas em que parte da energia cinética é transformada em outras formas de energia, como energia térmica, sonora ou deformação dos objetos. Nesse tipo de colisão, os objetos se juntam após o impacto. Um exemplo de colisão inelástica é o choque entre dois carros em uma estrada.
Por fim, as colisões parcialmente elásticas são aquelas em que parte da energia cinética é conservada e parte é dissipada. Isso resulta em uma combinação das características das colisões elásticas e inelásticas. Um exemplo de colisão parcialmente elástica é o impacto entre uma bola de borracha e uma superfície dura.
Em resumo, as colisões entre objetos em movimento podem ser classificadas em elásticas, inelásticas e parcialmente elásticas, dependendo do resultado do impacto. Cada tipo de colisão apresenta características específicas e pode ser observado em diferentes situações do cotidiano.
Identificando se a colisão é elástica ou inelástica: dicas e diferenciações importantes.
Quando se trata de identificar se uma colisão é elástica ou inelástica, é importante observar algumas dicas e diferenciações importantes. Em uma colisão elástica, a energia cinética total do sistema é conservada, enquanto em uma colisão inelástica, parte da energia cinética é dissipada na forma de calor, som e deformação dos corpos.
Para determinar se a colisão é elástica ou inelástica, é necessário analisar a conservação da energia cinética e da quantidade de movimento. Se a energia cinética total antes e depois da colisão for a mesma, então a colisão é elástica. Por outro lado, se a energia cinética total diminuir após a colisão, então ela é inelástica.
Em um choque inelástico em uma dimensão, os corpos se movem juntos após a colisão e a velocidade final é a mesma para ambos os corpos. Um exemplo comum de choque inelástico em uma dimensão é o de dois carros colidindo e ficando grudados um no outro após o impacto.
Em conclusão, ao observar a conservação da energia cinética e da quantidade de movimento, é possível identificar se uma colisão é elástica ou inelástica. Os choques inelásticos em uma dimensão são caracterizados pelo movimento conjunto dos corpos após a colisão.
Choques inelásticos: em uma dimensão e exemplos
As colisões inelásticas ou colisões inelásticas estão a uma curta e intensa interacção entre dois objectos, em que a quantidade de movimento é mantido, mas não a energia cinética, que é transformado percentagem alguma outra forma de energia.
Falhas ou colisões são de natureza frequente. Partículas subatômicas colidem em velocidades muito altas, enquanto muitos esportes e jogos consistem em colisões contínuas. Até as galáxias são capazes de colidir.

Na verdade, a quantidade de movimento é conservada em qualquer tipo de colisão, desde que as partículas que colidem formem um sistema isolado. Portanto, neste sentido, não há problema. Agora, os objetos têm energia cinética associada ao movimento que possuem. O que pode acontecer com essa energia quando atinge?
As forças internas que ocorrem durante o confronto entre os objetos são intensas. Quando se afirma que a energia cinética não é conservada, significa que é transformada em outros tipos de energia: por exemplo, energia sonora (uma colisão espetacular tem um som distinto).
Mais possibilidades de uso para energia cinética: calor por atrito e, é claro, a inevitável deformação de objetos ao colidir, como as carrocerias dos carros na figura acima.
Exemplos de colisões inelásticas
– Duas massas de plasticina que colidem e permanecem juntas, movendo-se como uma peça após o acidente.
– Uma bola de borracha que bate contra uma parede ou chão. A bola se deforma quando atinge a superfície.
Nem toda energia cinética é transformada em outros tipos de energia, com poucas exceções. Os objetos podem manter uma certa quantidade dessa energia. Mais tarde veremos como calcular a porcentagem.
Quando as peças colididas são unidas, a colisão é chamada perfeitamente inelástica, e ambas geralmente acabam se movendo juntas.
Colisões perfeitamente inelásticas em uma dimensão
A colisão da figura mostra dois objetos de diferentes massas m 1 e m 2 , movendo-se um para o outro com as velocidades v i1 e v i2 respectivamente. Tudo acontece na horizontal, ou seja, é uma colisão em uma dimensão, a mais fácil de estudar.

Os objetos colidem e depois permanecem unidos movendo-se para a direita. É uma colisão perfeitamente inelástica, portanto, mantenha a quantidade de movimento:
P o = P f
A quantidade de movimento é um vetor cujas unidades em SI são Ns. Na situação descrita, a notação vetorial pode ser dispensada no caso de colisões em uma dimensão:
mv o = mv f
A quantidade de movimento do sistema é a soma vetorial da quantidade de movimento de cada partícula.
m 1 v i1 + m 2 v i2 = (m 1 + m 2 ) v f
A velocidade final é dada por:
v f = (m 1 v i1 + m 2 v i2 ) / (m 1 + m 2 )
Coeficiente de Retorno
Há uma quantidade que pode indicar a elasticidade de uma colisão. Este é o coeficiente de restituição , que é definido como a razão negativa entre a velocidade relativa das partículas após a colisão e a velocidade relativa antes da colisão.
Seja u 1 e u 2 as velocidades respectivas das partículas inicialmente. E sejam v 1 e v 2 as respectivas velocidades finais. Matematicamente, o coeficiente de restituição pode ser expresso da seguinte forma:

– Se ε = 0 é equivalente a afirmar que v 2 = v 1 . Isso significa que as velocidades finais são as mesmas e a colisão é inelástica, como a descrita na seção anterior.
– Quando ε = 1 significa que as velocidades relativas antes e depois do acidente não mudam, nesse caso, o acidente é elástico.
– E se 0 <ε <1 parte da energia cinética da colisão é transformada em outra das energias mencionadas acima.
Como determinar o coeficiente de reembolso?
O coeficiente de restituição depende da classe de materiais envolvidos na colisão. Um teste muito interessante para determinar quão elástico é um material para fabricar bolas é soltar a bola em uma superfície fixa e medir a altura do ressalto.

Nesse caso, a placa fixa sempre tem a velocidade 0. Se esse índice for atribuído ao índice 1 e o índice da bola 2 permanecer:




No início, foi sugerido que toda a energia cinética pode ser transformada passando para outros tipos de energia. Afinal, a energia não é destruída. É possível que objetos que vieram com movimento colidam e se juntem para formar um único objeto que repousa repentinamente? Isso não é tão fácil de imaginar.
No entanto, vamos imaginar que isso acontece ao contrário, como em um filme visto ao contrário. Então o objeto estava inicialmente em repouso e depois explodiu, fragmentando-se em várias partes. Esta situação é perfeitamente possível: é uma explosão.
Portanto, uma explosão pode ser vista como uma colisão perfeitamente inelástica vista no tempo. A quantidade de movimento também é preservada e pode-se afirmar que:
P o = P f
Exemplos resolvidos
-Exercício 1
Sabe-se a partir das medições que o coeficiente de retorno do aço é 0,90. Uma bola de aço de 7 m de altura é jogada sobre uma placa fixa. Calcular:
a) Até que altura ele saltará.
b) Quanto tempo leva entre o primeiro contato com a superfície e o segundo.
Solução
a) A equação deduzida anteriormente na seção sobre a determinação do coeficiente de retorno é usada:
A altura h 2 é limpa :

0,90 2 . 7 m = 5.67 m
b) Para subir os 5,67 metros, uma velocidade dada por:

t max = V ou / g = (10,54 / 9,8) s = 1,08 s.
O tempo necessário para retornar é o mesmo; portanto, o tempo total para subir os 5,67 metros e retornar ao ponto de partida é o dobro do tempo máximo:
t voo = 2,15 s.
-Exercício 2
A figura mostra um bloco de madeira de massa M pendurado no restante comprimento do fio no modo pendular. Isso é chamado de pêndulo balístico e serve para medir a velocidade v da entrada de uma bala de massa m. Quanto maior a velocidade com que a bala atinge o bloco, maior o h aumentará.
A bala da imagem está embutida no bloco, portanto, é um choque totalmente inelástico.

Suponha que uma bala de 9,72 g atinja o bloco de massa 4,60 kg e, em seguida, a montagem suba para 16,8 cm a partir da posição de equilíbrio. Qual é a velocidade v da bala?
Solução
Durante a colisão, a quantidade de movimento é conservada e u f é a velocidade do conjunto, uma vez que a bala foi incorporada no bloco:
P o = P f
O bloco está inicialmente em repouso, enquanto o marcador atinge o alvo com velocidade v :
mv + M.0 = (m + M) u f

Não se sabe u f ainda, mas após a colisão energia mecânica é conservada, sendo a soma da energia potencial gravitacional e energia cinética U K:
Energia mecânica inicial = energia mecânica final
E mo = E mf
U o + K o = U f + K f
A energia potencial gravitacional depende da altura em que o conjunto atinge. Para a posição de equilíbrio, a altura inicial é aquela considerada como nível de referência, portanto:
U o = 0
Graças à bala, o conjunto possui energia cinética K o , que se torna energia potencial gravitacional quando o conjunto atinge sua altura máxima h . A energia cinética é dada por:
K = ½ mv 2
Inicialmente a energia cinética é:
K o = (1/2) (M + m) u f 2
Lembre-se de que a bala e o bloco já formam um único objeto de massa M + m . A energia potencial gravitacional quando atingem sua altura máxima é:
L f = (M + m) gh
Portanto:
K o = U f
(1/2) (M + m) u f 2 = (m + M) gh

-Exercício 3
O objeto da figura explode em três fragmentos: dois de massa igual me um maior de massa 2m. A figura mostra as velocidades de cada fragmento após a explosão. Qual foi a velocidade inicial do objeto?
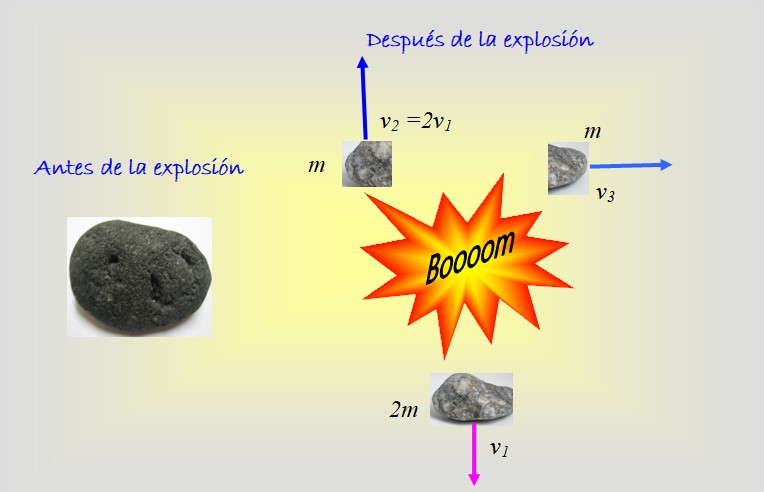
Solução
Esse problema requer o uso de duas coordenadas: x e y , porque dois dos fragmentos têm velocidades verticais, enquanto o restante tem velocidades horizontais.
A massa total do objeto é a soma da massa de todos os fragmentos:
M = m + m + 2m = 4m
A quantidade de movimento é preservada no eixo x e no eixo y, e é declarado separadamente:
- 4m u x = mv 3
- 4m u e = m. 2v 1 – 2m. v 1
Observe que o fragmento grande se move para baixo com a velocidade v1, para indicar esse fato que um sinal negativo foi colocado.
Da segunda equação segue-se imediatamente que u y = 0 e da primeira equação ux imediatamente:

Referências
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6 th . Ed Prentice Hall. 175-181
- Rex, A. 2011. Fundamentos de Física. Pearson 135-155.
- Serway, R., Vulle, C. 2011. Fundamentos de Física. 9 na Cengage Learning. 172-182
- Tipler, P. (2006) Física para Ciência e Tecnologia. 5º Ed. Volume 1. Editorial Reverté. 217-238
- Tippens, P. 2011. Física: Conceitos e Aplicações. 7ª Edição. MacGraw Hill. 185-195