Como multiplicar frações racionais com duas variáveis

Início » Ciência » Matemática » Como multiplicar frações racionais com duas variáveis

Os números racionais e as frações aparecem o tempo todo na vida real, mesmo quando a gente nem percebe: em finanças, na engenharia, na programação, nas medições do dia a dia e em praticamente qualquer situação em que seja preciso comparar partes de um todo. Quando essas frações envolvem letras (variáveis), como x e y, entramos no território da álgebra, onde saber multiplicar, somar e simplificar frações racionais com duas variáveis vira uma habilidade básica para conseguir avançar sem travar.

Muita gente, porém, sente um bloqueio enorme com matemática e álgebra, principalmente quando aparecem expressões como 2/(y – 8) = 1/(y – 2) e alguém fala para “multiplicar cruzado” ou “multiplicar pelo MMC”. Se você já ficou confuso sem saber quando multiplicar direto, quando usar regra de três ou quando aplicar o mínimo múltiplo comum, fique tranquilo: é totalmente normal. A ideia deste artigo é destrinchar com calma o que são números racionais, como funcionam as frações (inclusive com duas variáveis) e, passo a passo, mostrar a diferença entre multiplicar frações, multiplicar em cruz e usar o MMC, sempre com explicações claras e exemplos.

O que são números racionais e por que são tão importantes

Chamamos de números racionais todos os números que podem ser escritos na forma de fração a/b, em que a e b são inteiros e b é diferente de zero. Isso inclui desde frações “clássicas” como 3/4, até inteiros como 5 (que pode ser visto como 5/1) e diversos decimais que aparecem no cotidiano.

O conjunto dos números racionais é indicado pela letra Q, de “quotient” (quociente em inglês), justamente porque cada número racional é resultado de uma divisão entre inteiros. Essa forma fracionária permite representar com precisão quantidades que não são inteiras, como metade de um bolo (1/2), três oitavos de um caminho (3/8) ou 5% de juros (5/100).

Uma característica muito importante dos racionais é que eles formam um conjunto denso na reta real. Isso significa que, se você pegar dois números racionais quaisquer, sempre existe outro número racional entre eles. Por exemplo, entre 1/4 e 1/2 está 3/8; entre 2 e 3 está 5/2, e assim por diante, sem fim.

Outra ideia central é que todo número inteiro é, na verdade, um número racional, porque qualquer inteiro n pode ser representado como n/1. Dessa forma, quando você trabalha com racionais não está “abandonando” os inteiros; está, na verdade, ampliando o cenário para incluir inteiros, frações e decimais que podem ser escritos como fração.

Os números racionais também podem ser positivos, negativos ou até mesmo o próprio zero. O zero é racional porque pode ser escrito, por exemplo, como 0/5 ou 0/1. Já -3/7 é um racional negativo, enquanto 4/9 é positivo. Esse leque de possibilidades é o que faz os racionais serem tão usados em equações, estatística, medições e modelagem de fenômenos na ciência.

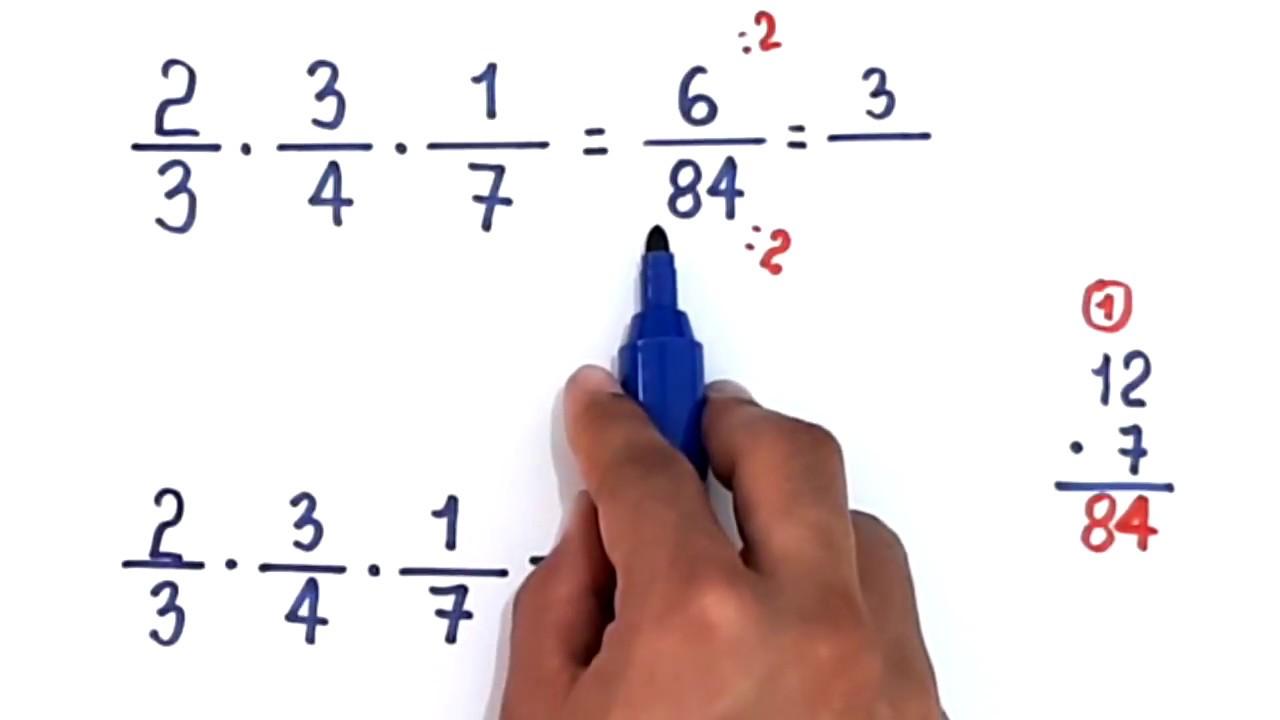
Frações, numerador, denominador e frações equivalentes

Uma fração nada mais é do que a representação de uma parte de um todo. Quando escrevemos a/b, o número de cima (a) é chamado de numerador e o número de baixo (b), de denominador. O denominador indica em quantas partes o inteiro foi dividido, e o numerador indica quantas dessas partes estão sendo consideradas.

Numerador é o número que fica acima da barra de fração e mostra quantas partes você tem. Se você divide um bolo em 8 fatias e come 3, pode escrever a quantidade de bolo que comeu como 3/8: o numerador é 3 e indica que você pegou três partes.

Denominador é o número que aparece abaixo da barra e aponta em quantas partes o inteiro foi cortado. No exemplo do bolo, 8 é o denominador, pois o todo foi dividido em 8 fatias iguais. Se o denominador é 4, isso quer dizer que o inteiro foi particionado em quatro partes, cada uma equivalente a um quarto do todo.

Frações equivalentes são frações que representam a mesma quantidade, mesmo com números diferentes. Por exemplo, 1/2, 2/4 e 4/8 são equivalentes, pois todas indicam “metade” de algo. Obtemos frações equivalentes multiplicando ou dividindo numerador e denominador pelo mesmo número não nulo.

A simplificação de frações é justamente o processo de reduzir uma fração à sua forma mais simples, isto é, encontrar uma fração equivalente em que numerador e denominador não possam mais ser divididos pelo mesmo número (diferente de 1 e -1). Usamos o maior divisor comum (MDC) para isso: dividimos o numerador e o denominador pelo MDC.

Por exemplo, para simplificar 8/12, analisamos os divisores de 8 e 12. O maior divisor comum entre eles é 4. Dividindo numerador e denominador por 4, obtemos 2/3, que é a forma irredutível de 8/12, pois 2 e 3 não têm outro divisor comum além de 1.

Decimais finitos, decimais periódicos e a relação com racionais

Qualquer número racional pode ser representado também em forma decimal. Em alguns casos, essa representação termina em um certo ponto (decimal finita); em outros, os dígitos decimais se repetem para sempre (decimal periódica).

Uma decimal finita é aquela que tem um número limitado de casas decimais. Exemplos clássicos são 0,5 (que corresponde a 1/2) ou 0,75 (equivalente a 3/4). Normalmente, essas frações têm denominadores que podem ser escritos como potências de 2 e 5 (por exemplo, 10, 100, 1000, etc.).

Já uma decimal periódica é um decimal que se repete indefinidamente, como 0,333… para 1/3 ou 0,666… para 2/3. Nesses casos, há um bloco de dígitos que se repete ao infinito, o que chamamos de período. Apesar de não “terminarem”, esses decimais ainda representam números racionais, pois correspondem a frações bem definidas.

Por isso, dizemos que todos os decimais finitos e todos os decimais periódicos são racionais, enquanto os decimais que não repetem padrão nenhum (como o valor de π) são irracionais. Os racionais, então, cobrem todas as frações, inteiros e decimais que podem ser associados a uma fração de inteiros.

Na prática, essa distinção é muito utilizada em cálculos e medições. Quando queremos representar algo com total precisão em matemática pura ou em programação, muitas vezes preferimos manter a forma fracionária, pois o decimal pode esconder a verdadeira natureza do número (finito ou periódico).

Operações com números racionais: soma, produto e divisão de frações

Um ponto fundamental sobre os números racionais é que eles são fechados em relação a certas operações, ou seja, se você somar, subtrair ou multiplicar dois racionais, o resultado também será um número racional. Isso é uma das bases para trabalhar com frações em álgebra e na teoria dos números.

Quando falamos de soma de frações, normalmente precisamos de um denominador comum. Para somar a/b e c/d, a ideia é reescrever as duas frações com o mesmo denominador e, então, somar apenas os numeradores, mantendo esse denominador comum.

Um método padrão para somar frações a/b e c/d é usar o produto bd como denominador comum. Assim, reescrevemos a/b como (a·d)/(b·d) e c/d como (c·b)/(d·b). Depois de ter as duas frações com o mesmo denominador, somamos os numeradores: (a·d + c·b)/(b·d). Dependendo do caso, ainda é possível simplificar o resultado.

No caso do produto de frações, a regra é bem mais direta: para multiplicar a/b por c/d, basta multiplicar os numeradores entre si e os denominadores entre si, obtendo (a·c)/(b·d). Em seguida, se possível, simplificamos a fração resultante usando o MDC.

Na divisão de frações, utilizamos a ideia da fração inversa. Para dividir a/b por c/d (com c/d diferente de zero), multiplicamos a/b pelo inverso de c/d, que é d/c. Assim, a/b ÷ c/d = a/b · d/c = (a·d)/(b·c). De novo, é possível simplificar o resultado se houver fatores comuns entre numerador e denominador.

Multiplicar frações racionais com duas variáveis

Quando entram variáveis como x e y nas frações, a regra de multiplicação continua exatamente a mesma. A única diferença é que, em vez de multiplicar apenas números, multiplicamos expressões algébricas, respeitando as propriedades da álgebra.

Suponha que você queira multiplicar (2x)/(3y) por (5y)/(4x). O procedimento é idêntico ao caso numérico: multiplicamos os numeradores (2x·5y) e os denominadores (3y·4x). O resultado inicial é (10xy)/(12xy). Agora, ocorre algo interessante: x e y aparecem tanto no numerador quanto no denominador, então podemos simplificar.

Fatorando e cancelando termos comuns, dividimos numerador e denominador por xy, obtendo 10/12. Em seguida, podemos simplificar 10/12 dividindo por 2, o MDC de 10 e 12, resultando em 5/6. Assim, mesmo com variáveis, o produto de frações racionais segue o padrão “numerador com numerador, denominador com denominador”, e a simplificação leva em conta fatores numéricos e variáveis.

Outro ponto importante é entender que as variáveis não precisam ser iguais para aplicarmos a regra. Em (3a)/(2b) · (4c)/(5d), o resultado será (3a·4c)/(2b·5d) = (12ac)/(10bd). Caso surjam letras repetidas em cima e embaixo, podemos simplificar; se não, deixamos a resposta nessa forma ou fatoramos conforme o contexto do problema.

Na prática, multiplicar frações racionais com duas variáveis é essencial em expressões algébricas mais complicadas, como nas equações que surgem em problemas de física, economia ou mesmo em questões de vestibulares e concursos. Dominar esse processo facilita bastante o trabalho com equações que misturam números e letras.

Multiplicar cruzado x multiplicar direto: qual a diferença?

Uma dúvida muito comum é saber quando usar a chamada “multiplicação cruzada” e quando apenas multiplicar frações normalmente. A grande diferença é o tipo de situação em que cada técnica é aplicada.

Multiplicar direto é o que fazemos quando estamos apenas calculando o produto de duas frações. Por exemplo, em (2/3) · (4/5), simplesmente fazemos (2·4)/(3·5) = 8/15. Não há necessidade de cruzar nada, pois não é uma igualdade de frações, e sim uma multiplicação comum.

A multiplicação cruzada aparece, principalmente, quando temos uma igualdade entre duas frações, ou seja, uma equação do tipo a/b = c/d, em que b e d são diferentes de zero. Nessa configuração, podemos usar o fato de que a·d = b·c. Esse “cruzamento” serve para eliminar os denominadores e transformar a equação fracionária em uma equação com inteiros ou expressões mais simples.

Por exemplo, se temos 2/(y − 8) = 1/(y − 2), estamos diante de uma equação entre duas frações com variáveis no denominador. A multiplicação cruzada nos permite escrever 2·(y − 2) = 1·(y − 8). Depois disso, resolvemos a equação normalmente: 2y − 4 = y − 8, o que leva a y = −4, lembrando sempre de verificar se esse valor não zera nenhum denominador original.

Portanto, multiplicação cruzada é uma ferramenta para resolver equações entre frações, não para multiplicar frações em geral. Quando a tarefa é apenas encontrar o produto de duas frações, seguimos a regra do produto direto; quando a tarefa é resolver uma igualdade entre frações, a multiplicação em cruz é uma forma prática de “eliminar” os denominadores.

Usar MMC ou multiplicação cruzada: o que muda em equações com frações?

Outra técnica muito citada pelos professores é multiplicar toda a equação pelo mínimo múltiplo comum (MMC) dos denominadores. Essa ideia é conceitualmente parecida com a multiplicação cruzada, mas funciona de maneira mais geral, inclusive quando há mais de duas frações na mesma equação.

Quando você tem uma equação que envolve várias frações, o objetivo é se livrar dos denominadores. Para isso, escolhemos um número (ou expressão algébrica) que seja múltiplo de todos os denominadores e multiplicamos cada termo da equação por esse mesmo valor. Como resultado, as frações “somem”, pois os denominadores acabam sendo cancelados.

No caso da equação 2/(y − 8) = 1/(y − 2), o MMC dos denominadores (y − 8) e (y − 2) é o próprio produto (y − 8)(y − 2), já que são expressões distintas. Multiplicando toda a equação por (y − 8)(y − 2), obtemos: (y − 8)(y − 2) · 2/(y − 8) = (y − 8)(y − 2) · 1/(y − 2).

Ao simplificar, o (y − 8) cancela com o denominador do primeiro termo e o (y − 2) cancela com o denominador do segundo termo, resultando em 2·(y − 2) = 1·(y − 8). Observe que chegamos na mesma expressão obtida pela multiplicação cruzada. Ou seja, nesse tipo de equação simples, multiplicar cruzado e multiplicar pelo MMC dão, na prática, o mesmo resultado.

A grande vantagem do método do MMC aparece quando lidamos com mais de duas frações ou com denominadores mais complexos, pois ele oferece um procedimento sistemático: encontrar o MMC, multiplicar toda a equação por ele e simplificar. Em muitas situações de álgebra, essa é a abordagem preferida porque generaliza bem.

Propriedades dos números racionais e seu papel na álgebra

Os números racionais obedecem a um conjunto de propriedades que tornam as contas previsíveis e organizadas. Isso é essencial na álgebra, onde manipulamos expressões simbólicas baseadas nessas regras.

Entre as propriedades mais importantes estão a comutatividade, a associatividade e a distributividade. A comutatividade diz que a ordem da soma ou do produto não altera o resultado (a + b = b + a, a·b = b·a). A associatividade garante que podemos agrupar termos de maneiras diferentes sem mudar o valor (a + (b + c) = (a + b) + c). Já a distributividade permite espalhar um fator sobre uma soma, como em a·(b + c) = a·b + a·c.

Também temos a existência de elementos neutros para soma e multiplicação. O zero é o neutro da soma (a + 0 = a), e o 1 é o neutro da multiplicação (a·1 = a). Para cada número racional não nulo, existe ainda um inverso multiplicativo, isto é, um número que, multiplicado por ele, dá 1. No caso de a/b, o inverso é b/a.

Essas propriedades são a base de manipulações algébricas mais elaboradas, como simplificar expressões, resolver equações com frações, fatorar polinômios e tratar de proporções. Nos problemas que envolvem frações racionais com duas variáveis, estamos praticamente o tempo inteiro usando essas regras, muitas vezes de forma implícita.

Em álgebra, trabalhamos com símbolos que representam números racionais e irracionais, mas as regras para lidar com frações em geral vêm, principalmente, dessas propriedades dos racionais. É por isso que entender bem as operações com frações no ensino básico facilita tanto a vida em conteúdos mais avançados, como funções e cálculo.

Aplicações dos números racionais no cotidiano e em outras áreas da matemática

No dia a dia, encontramos números racionais em quase qualquer contexto onde há divisões, proporções ou comparações entre partes. Ao medir ingredientes de uma receita, ao dividir uma conta entre amigos, ao ler uma taxa de juros no banco ou ao analisar um gráfico de pesquisa, invariavelmente estamos lidando com frações.

Na estatística, racionais aparecem quando calculamos médias, proporções e probabilidades. Se, em uma pesquisa, 3 de cada 5 pessoas preferem chocolate a baunilha, representamos isso como 3/5. Essa fração pode ser convertida para decimal (0,6) ou porcentagem (60%), mas a essência racional continua ali.

No campo das finanças, juros e descontos são frequentemente expressos como frações ou porcentagens. Uma taxa de 5% ao ano equivale a 5/100, e ao aplicar essa fração sobre um valor (como R$ 100), obtemos o rendimento correspondente (R$ 5 de juros, totalizando R$ 105).

Na engenharia e nas ciências em geral, números racionais são fundamentais para representar relações entre grandezas, como razões de escalas, densidades, concentrações ou velocidades médias. Muitas fórmulas usam frações envolvendo variáveis, e é aí que dominar frações racionais com duas variáveis se torna ainda mais útil.

Na programação e na computação, embora os computadores trabalhem frequentemente com aproximações decimais (ponto flutuante), a teoria por trás da representação exata de muitos valores está ligada aos números racionais, especialmente em algoritmos que exigem alta precisão e evitam arredondamentos prematuros.

Aspectos históricos e teóricos dos números racionais

O estudo dos números racionais tem uma longa trajetória na história da matemática. Desde a antiguidade, civilizações já trabalhavam com frações para lidar com partilhas de terrenos, distribuição de alimentos e problemas de comércio.

Euclides, em sua obra clássica Os Elementos, dedicou diversas partes à teoria dos números e às propriedades das frações. Ele também discutiu o surgimento dos números irracionais, mostrando que nem todas as quantidades podiam ser expressas como frações de inteiros, o que marcou um grande avanço conceitual.

Diophantus, muitas vezes chamado de “pai da álgebra”, aprofundou o estudo de equações que envolviam frações e inteiros. Seu trabalho abriu caminho para uma visão mais simbólica da matemática, onde equações com frações racionais passaram a ser tratadas de forma sistemática.

No século XVII, matemáticos como René Descartes e John Wallis contribuíram para formalizar a notação e o tratamento das frações. A introdução do sistema de coordenadas e o desenvolvimento do cálculo exigiram uma linguagem mais clara para lidar com números racionais em contextos geométricos e analíticos.

Já no século XX, nomes como Paul Erdős e John von Neumann exploraram os racionais conectando-os a outras áreas avançadas, como teoria dos conjuntos, lógica e topologia. Eles ajudaram a estabelecer pontes entre o conjunto Q e outras estruturas matemáticas, reforçando o papel central dos racionais na teoria dos números.

Hoje, a teoria dos números continua estudando em profundidade as propriedades dos racionais e sua relação com os irracionais, com impactos em criptografia, codificação de dados, análise de algoritmos e vários outros campos que, à primeira vista, parecem distantes de simples frações, mas que dependem delas em nível teórico.

Perceber como um conceito aparentemente simples, como “fração de dois inteiros”, deu origem a tantas ideias é uma boa forma de valorizar o estudo dos racionais. Do aprendizado escolar às aplicações de ponta na ciência e na tecnologia, eles formam uma espécie de ponte entre o mundo concreto das medições e o universo abstrato da matemática.

Quando você entende que números racionais englobam frações, inteiros, decimais finitos e periódicos, e aprende a somar, multiplicar, simplificar e resolver equações com eles, inclusive com duas variáveis, passa a enxergar a matemática com outros olhos. Técnicas como multiplicação direta de frações, multiplicação cruzada em equações e uso de MMC deixam de ser “truques decorados” e viram ferramentas lógicas, que fazem sentido dentro de um sistema bem organizado de regras e propriedades.