A constante de integração é um termo fundamental na resolução de integrais indefinidas. Ela representa uma constante desconhecida que é adicionada à solução geral de uma integral, já que ao derivar uma constante não obtém-se um resultado diferente de zero. A constante de integração é importante, pois pode representar diferentes soluções para um mesmo problema.
No cálculo da constante de integração, geralmente é utilizado o método de avaliar a integral indefinida e em seguida adicionar a constante de integração. Para encontrar o valor específico da constante, é necessário utilizar informações adicionais fornecidas no problema.
Alguns exemplos de integrais com constantes de integração são:
– ∫x² dx = (1/3)x³ + C
– ∫sen(x) dx = -cos(x) + C
– ∫e^x dx = e^x + C
Dessa forma, a constante de integração desempenha um papel importante na resolução de integrais, garantindo a inclusão de todas as possíveis soluções para um problema.
Método simples para calcular a integral de uma constante em poucos passos.
Para calcular a integral de uma constante, basta lembrar que a integral de uma constante é igual à constante multiplicada pela variável de integração mais a constante de integração. Em outras palavras, a integral de k é igual a kx + C, onde k é a constante e C é a constante de integração.
Por exemplo, se quisermos calcular a integral de 3, basta aplicar a fórmula acima. A integral de 3 é igual a 3x + C, onde x é a variável de integração e C é a constante de integração.
Portanto, o método simples para calcular a integral de uma constante em poucos passos é multiplicar a constante pela variável de integração e adicionar a constante de integração ao resultado.
Se tivermos a integral de 5, por exemplo, o cálculo seria o seguinte: a integral de 5 é igual a 5x + C, onde x é a variável de integração e C é a constante de integração.
Em resumo, calcular a integral de uma constante é um processo simples que envolve apenas multiplicar a constante pela variável de integração e adicionar a constante de integração ao resultado. É importante lembrar sempre de incluir a constante de integração ao calcular integrais.
Significado do cálculo integral: descubra a definição desse conceito matemático fundamental.
O cálculo integral é um conceito fundamental da matemática que envolve o cálculo de áreas sob curvas. Ele é utilizado para determinar a área entre uma curva e o eixo x em um intervalo específico, bem como para calcular volumes de sólidos de revolução e muitas outras aplicações na ciência e engenharia.
A constante de integração é um termo que aparece ao resolver uma integral indefinida. Ela é representada por “+ C” e é adicionada à resposta da integral para levar em conta todas as possíveis soluções da equação diferencial original.
Para calcular a constante de integração, é necessário resolver a integral indefinida e adicionar a constante “+ C” no final da resposta. Essa constante é fundamental para garantir que todas as soluções da equação diferencial sejam consideradas.
Um exemplo simples de constante de integração é a integral de x^2, que resulta em (1/3)x^3 + C. Neste caso, a constante de integração “+ C” representa todas as possíveis soluções da integral indefinida, já que não há informação suficiente para determinar um valor específico para a constante.
Em resumo, a constante de integração é essencial ao resolver integrais indefinidas, pois garante que todas as soluções da equação diferencial sejam consideradas. Ela é representada por “+ C” e é adicionada ao final da resposta da integral.
Significado e importância da constante de integração na resolução de problemas de integração.
A constante de integração é um termo que surge ao resolver problemas de integração na matemática. Ela representa uma parte da solução que não pode ser determinada apenas com base na função a ser integrada. Em outras palavras, a constante de integração é uma constante arbitrária que é adicionada à resposta da integral indefinida.
A importância da constante de integração reside no fato de que ela permite considerar todas as possíveis soluções de uma integral indefinida. Sem a inclusão da constante de integração, a solução seria incompleta e não abrangeria todas as possibilidades. Portanto, a constante de integração é essencial para garantir uma solução abrangente e correta ao resolver problemas de integração.
Para calcular a constante de integração, basta adicionar a letra “C” à resposta da integral indefinida. Por exemplo, se a integral de uma função for x^2, a solução seria x^3/3 + C, onde C é a constante de integração.
Em resumo, a constante de integração desempenha um papel fundamental na resolução de problemas de integração, garantindo que todas as possíveis soluções sejam consideradas. É importante lembrar de incluir a constante de integração ao resolver integrais para obter uma resposta completa e precisa.
Como encontrar a fórmula da integral em cálculos matemáticos?
A fórmula da integral em cálculos matemáticos é uma ferramenta essencial para resolver problemas de integração. Para encontrar essa fórmula, é necessário seguir alguns passos. Primeiramente, é preciso identificar a função a ser integrada e determinar os limites de integração. Em seguida, aplica-se o método de integração adequado, como integração por partes, substituição trigonométrica ou frações parciais.
Após realizar a integração, obtemos a resposta em forma de uma expressão matemática. No entanto, é importante lembrar que toda integral possui uma constante de integração, representada pela letra “C”. Essa constante surge devido ao fato de que a derivada de uma constante é sempre zero.
Para determinar a constante de integração, é necessário ter informações adicionais sobre o problema em questão. Por exemplo, se forem fornecidas condições iniciais ou limites específicos, podemos usar esses dados para encontrar o valor da constante.
Em resumo, a constante de integração é um termo fundamental na resolução de integrais, pois representa a indeterminação que surge durante o processo de integração. Ao entender o significado e a importância dessa constante, podemos obter resultados mais precisos e completos em nossos cálculos matemáticos.
Constante de integração: significado, cálculo e exemplos
A constante de integração é um valor agregado para o cálculo das antiderivadas ou integrais, serve para representar as soluções que compõem a primitiva de uma função. Expressa uma ambiguidade inerente em que qualquer função possui um número infinito de primitivas.
Por exemplo, se a função for aceita: f (x) = 2x + 1 e obtemos sua antiderivada:
∫ (2x + 1) dx = x 2 + x + C ; Onde C é a constante de integração e representa graficamente a tradução vertical entre as infinitas possibilidades do primitivo. É correto dizer que (x 2 + x) é uma das primitivas de f (x).
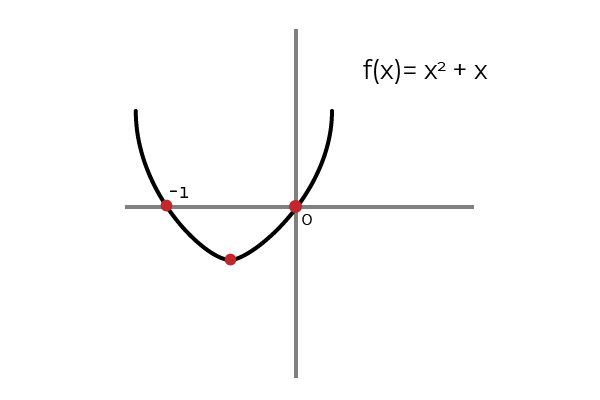
Da mesma forma, a (x 2 + x + C ) pode ser definido como o primitivo de f (x).
Propriedade inversa
Pode-se notar que, ao derivar a expressão (x 2 + x), é obtida a função f (x) = 2x + 1. Isso ocorre devido à propriedade inversa existente entre a derivação e a integração de funções. Esta propriedade permite obter fórmulas de integração a partir da diferenciação. O que permite a verificação de integrais através dos mesmos derivados.
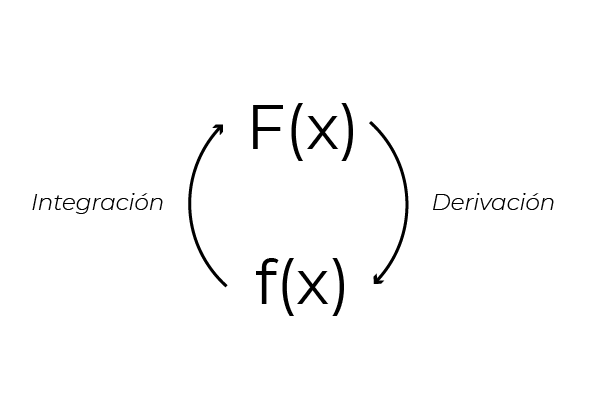
No entanto (x 2 + x) não é a única função cuja derivada é igual a (2x + 1).
- d ( x 2 + x) / dx = 2x + 1
- d ( x 2 + x + 1) / dx = 2x + 1
- d ( x 2 + x + 2) / dx = 2x + 1
- d ( x 2 + x + 3) / dx = 2x + 1
- d ( x 2 + x + C ) / dx = 2x + 1
Onde 1, 2, 3 e 4 representam primitivas particulares de f (x) = 2x + 1. Enquanto 5 representa a integral indefinida ou primitiva de f (x) = 2x + 1.

As primitivas de uma função são alcançadas através do processo de antiderivação ou integral. Onde F será uma primitiva de f se o seguinte for verdadeiro
- y = ∫ f (x) dx = F (x) + C; C = constante de integração
- F ‘(x) = f (x)
Aprecia-se que uma função tenha apenas uma derivada, diferentemente de suas infinitas primitivas resultantes da integração.
A integral indefinida
∫ f (x) dx = F (x) + C
Corresponde a uma família de curvas com o mesmo padrão, que experimentam incongruência no valor das imagens de cada ponto (x, y). Cada função que atende a esse padrão será uma primitiva individual e o conjunto de todas as funções é conhecido como integral indefinido.
O valor da constante de integração será o que diferencia cada função na prática.
A constante de integração sugere uma mudança vertical em todos os gráficos que representam as primitivas de uma função. Onde o paralelismo entre eles é observado e o fato de que C é o valor do deslocamento.
De acordo com práticas comuns, a constante de integração é denotada pela letra “C” após uma soma, embora na prática seja indiferente se a constante é adicionada ou subtraída. Seu valor real pode ser encontrado de várias formas, de acordo com diferentes condições iniciais .
Outros significados da constante de integração
Já se falou de como a constante de integração é aplicada no ramo do cálculo integral ; Representando uma família de curvas que definem a integral indefinida. Mas muitas outras ciências e ramos atribuíram valores muito interessantes e práticos da constante de integração, o que facilitou o desenvolvimento de vários estudos.
Na física, a constante de integração pode assumir vários valores, dependendo da natureza dos dados. Um exemplo muito comum é conhecer a função V (t) que representa a velocidade de uma partícula versus o tempo t. Sabe-se que ao calcular uma primitiva de V ( t) é obtida a função R (t) que representa a posição da partícula versus o tempo.
A constante de integração representará o valor da posição inicial, ou seja, no tempo t = 0.
Da mesma forma, se a função A (t) que representa a aceleração da partícula versus o tempo é conhecida. A primitiva de A (t) resultará na função V (t), onde a constante de integração será o valor da velocidade inicial V 0 .
Em economia , obtendo através da integração o primitivo de uma função de custo. A constante de integração representará os custos fixos. E tantas outras aplicações que merecem cálculo diferencial e integral.
Como é calculada a constante de integração?
Para o cálculo da constante de integração, sempre será necessário conhecer as condições iniciais . Quais são os responsáveis por definir qual das primitivas possíveis é a correspondente.
Em muitas aplicações, é tratada como uma variável independente do tempo (t), onde a constante C recebe os valores que definem as condições iniciais do caso particular.
Se o exemplo inicial for tomado: ∫ (2x + 1) dx = x 2 + x + C
Uma condição inicial válida pode ser condicionar o gráfico a passar por uma coordenada específica. Por exemplo, sabe-se que o primitivo (x 2 + x + C) passa pelo ponto (1, 2)
F (x) = x 2 + x + C; esta é a solução geral
F (1) = 2
Substituímos a solução geral nessa igualdade
F (1) = (1) 2 + (1) + C = 2
De onde é fácil deduzir que C = 0
Assim, a primitiva correspondente para este caso é F (x) = x 2 + x
Existem vários tipos de exercícios numéricos que trabalham com constantes de integração . De fato, o cálculo diferencial e integral não deixa de ser aplicado na pesquisa atual. Em diferentes níveis acadêmicos, eles podem ser encontrados; do cálculo inicial, passando pela física, química, biologia, economia, entre outros.
Também pode ser visto no estudo de equações diferenciais , onde a constante de integração pode levar valores e soluções diferentes, devido às múltiplas derivações e integrações que são feitas nesta matéria.
Exemplos
Exemplo 1
- Um canhão localizado a 30 metros de altura dispara um projétil verticalmente para cima. Sabe-se que a velocidade inicial do projétil é de 25 m / s. Determine:
- A função que define a posição do projétil em relação ao tempo.
- A hora do voo ou instante em que a partícula toca o solo.
Sabe-se que em um movimento retilíneo uniformemente variado a aceleração é um valor constante. É o caso do lançamento do projétil, onde a aceleração será por gravidade
g = – 10 m / s 2
Sabe-se também que a aceleração é a segunda derivada da posição, o que indica uma dupla integração na resolução do exercício, obtendo assim duas constantes de integração.
A (t) = -10
V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C 1
As condições iniciais do exercício indicam que a velocidade inicial é V 0 = 25 m / s. Essa é a velocidade no instante do tempo t = 0. Dessa forma, é cumprido que:
V (0) = 25 = -10 (0) + C 1 e C 1 = 25
A função de velocidade que está sendo definida
V (t) = -10t + 25; A semelhança com a fórmula MRUV pode ser observada (V f = V 0 + axt)
De maneira homóloga, a função de velocidade é integrada para obter a expressão que define a posição:
R (t) = ∫V (t) dt = ∫ (-10t + 25) dt = -5t 2 + 25t + C 2
R (t) = -5T 2 + 25t + C 2 (posição original)
A posição inicial R (0) = 30 m é conhecida. Então a primitiva particular do projétil é calculada.
R (0) = 30m = -5 (0) 2 + 25 (0) + C 2 . Onde C 2 = 30
A primeira seção é resolvida desde que R (t) = -5t 2 + 25t + 30 ; Esta expressão é deslocamento homóloga MRUV fórmula R (t) = R 0 + V 0 t – gt 2 /2
Para a segunda seção, a equação quadrática deve ser resolvida: -5t 2 + 25t + 30 = 0
Como isso condiciona a partícula para alcançar o solo (posição = 0)
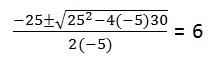
Na verdade, a equação do 2º grau nos dá 2 soluções T: {6, -1}. O valor t = -1 é ignorado porque são unidades de tempo cujo domínio não inclui números negativos.
Dessa forma, a segunda seção em que o tempo de vôo é igual a 6 segundos é resolvida.
Exemplo 2
- Encontre a primitiva f (x) que atende às condições iniciais:
- f (x) = 4; f ‘(2) = 2; f (0) = 7
Com as informações da segunda derivada f ” (x) = 4, o processo de antiderivação começa
f (x) = ∫f (x) dx
∫4 dx = 4x + C 1
Então, conhecendo a condição f ‘(2) = 2, proceda:
4 (2) C + 1 = 2
C 1 = -6 e f ‘(x) = 4x – 8
Prosseguimos da mesma maneira para a segunda constante de integração
f (x) = ∫f (x) dx
∫ (4x – 8) dx = 2x 2 – 8x + C 2
A condição inicial f (0) = 7 é conhecida e prosseguimos:
2 (0) 2 – 8 (0) + C 2 = 7
C 2 = 7 ef (x) = 2x 2 – 8x + 7
- f (x) = x 2 ; f ‘(0) = 6; f (0) = 3
De maneira semelhante ao problema anterior, definimos as primeiras derivadas e a função original a partir das condições iniciais.
f (x) = ∫f (x) dx
∫ (x 2 ) dx = (x 3 /3) + C 1
Com a condição f ‘(0) = 6, proceda:
(0 3 /3) + C 1 = 6; Quando C 1 = 6 e F ‘(x) = (x 3 /3) + 6
Então a segunda constante de integração
f (x) = ∫f ‘(x) dx
∫ [(x 3 /3) + 6] dx = (x 4 /12) + 6x + C 2
A condição inicial f (0) = 3 é conhecida e prossiga:
[(0) 4 /12] + 6 (0) + C 2 = 3; Onde C 2 = 3
O primitivo particular é assim obtido
f (x) = (x 4 /12) + 6x + 3
Exemplo 3
- Defina as funções primitivas dadas as derivadas e um ponto no gráfico:
- dy / dx = 2x – 2 Passando pelo ponto (3, 2)
É importante lembrar que as derivadas se referem à inclinação da linha tangente à curva em um determinado ponto. Onde não é correto supor que o gráfico da derivada toque o ponto indicado, pois pertence ao gráfico da função primitiva.
Dessa maneira, expressamos a equação diferencial da seguinte maneira:
dy = ( 2x – 2) dx ; então, ao aplicar os critérios de antiderivação, você tem:
∫dy = ∫ (2x – 2) dx
y = x 2 – 2x + C
Aplicando a condição inicial:
2 = (3) 2 – 2 (3) + C
C = -1
Você obtém: f (x) = x 2 – 2x – 1
- dy / dx = 3x 2 – 1 Que passa pelo ponto (0, 2)
Expressamos a equação diferencial da seguinte forma:
dy = ( 3x 2 – 1) dx ; então, ao aplicar os critérios de antiderivação, você tem:
∫dy = ∫ ( 3x 2 – 1) dx
y = x 3 – x + C
Aplicando a condição inicial:
2 = (0) 2 – 2 (0) + C
C = 2
Você obtém: f (x) = x 3 – x + 2
Exercícios propostos
Exercício 1
- Encontre a primitiva f (x) que atende às condições iniciais:
- f (x) = x; f ‘(3) = 1; f (2) = 5
- f (x) = x + 1; f ‘(2) = 2; f (0) = 1
- f ” (x) = 1; f ‘(2) = 3; f (1) = 10
- f (x) = -x; f ‘(5) = 1; f (1) = -8
Exercício 2
- Um balão que sobe a uma velocidade de 16 pés / s libera um saco de areia a uma altura de 64 pés acima do nível do solo.
- Definir o tempo de vôo
- Qual será o vetor V f quando tocar o chão?
Exercício 3
- A figura mostra o gráfico de aceleração – tempo de um carro se movendo na direção positiva do eixo x. O carro estava viajando a uma velocidade constante de 54 km / h quando o motorista acionou os freios para parar em 10 segundos. Determine:
- A aceleração inicial do carro
- A velocidade do carro em t = 5s
- O deslocamento do carro durante a frenagem

Exercício 4
- Defina as funções primitivas dadas as derivadas e um ponto no gráfico:
- dy / dx = x O que acontece através do ponto (-1, 4)
- dy / dx = -x 2 + 1 que passa pelo ponto (0, 0)
- dy / dx = -x + 1 que passa pelo ponto (-2, 2)
Referências
- Cálculo integral. Integral indefinido e métodos de integração. Wilson, Velásquez Bastidas. Universidade de Magdalena 2014
- Stewart, J. (2001). Cálculo de uma variável. Transcendentes Antecipados México: Thomson Learning.
- Jiménez, R. (2011). Matemática VI. Cálculo integral. México: Pearson Education.
- Física I. Mc Graw Hill