- La parità distingue funzioni pari (simmetriche in y) e dispari (simmetriche all’origine) e ne governa somma e prodotto.
- Le onde si classificano per natura, dimensioni di propagazione e direzione di vibrazione, con grandezze chiave λ, f, T e v.
- I fenomeni ondulatori principali includono riflessione, rifrazione, polarizzazione, diffrazione, interferenza e risonanza.
- Un prontuario di formule (moto, energia, circuiti, EM) permette di applicare rapidamente i concetti a esercizi e casi reali.
Quando si parla di “par” nel contesto fisico-matematico, ci si riferisce alla parità delle funzioni: una proprietà di simmetria che semplifica calcoli, interpretazioni grafiche e persino l’analisi di fenomeni ondulatori. In molte applicazioni di fisica e ingegneria, riconoscere una funzione come pari o dispari consente di prevedere il comportamento dei sistemi e ridurre il lavoro computazionale grazie a regole eleganti di somma, prodotto e trasformazioni.
Allo stesso tempo, gran parte della fisica elementare ruota attorno a onde, oscillazioni e grandi famiglie di formule (cinematica, dinamica, termologia, elettromagnetismo…). Per questo motivo, oltre a chiarire la definizione di funzione pari e dispari con esempi e proprietà, integreremo una panoramica strutturata sui principali concetti di ondulatoria e un ricco promemoria delle formule fondamentali di fisica, completate da esempi pratici e fenomeni reali (come riflessione, rifrazione o risonanza).
Funzioni pari e dispari: definizione, simmetrie ed esempi
Una funzione si dice pari se soddisfa la condizione f(−x) = f(x) per ogni x del suo dominio; questo implica che il suo grafico è simmetrico rispetto all’asse y. Viceversa, una funzione è dispari se f(−x) = −f(x), e il suo grafico è simmetrico rispetto all’origine del sistema cartesiano; in sostanza, ruotando di 180° intorno all’origine si ottiene lo stesso disegno.
Per rendere l’idea: cos(x) è pari (cos(−x) = cos x), mentre sin(x) è dispari (sin(−x) = −sin x). Una funzione come f(x) = x2 è chiaramente pari, mentre g(x) = x3 è un prototipo di funzione dispari; queste simmetrie risultano immediatamente visibili nei grafici.
Costanti e funzione nulla: ogni funzione costante f(x) = c è pari (la simmetria rispetto all’asse y è ovvia); l’unica funzione contemporaneamente pari e dispari è la funzione nulla f(x) = 0, poiché soddisfa entrambe le definizioni.
Per visualizzare numericamente, ecco un piccolo schema per una funzione dispari come f(x) = x:
| x | f(x) |
|---|---|
| −1 | −1 |
| 0 | 0 |
| 1 | 1 |
Si nota che f(−1) = −f(1), confermando la parità dispari; la stessa idea vale per funzioni pari (ad esempio f(x) = x2 produce valori uguali in ±x).
Proprietà operative della parità: somme, prodotti e scalari
Le regole algebriche della parità sono preziose per semplificare calcoli. Se f e g sono entrambe pari, allora f+g è pari; se sono entrambe dispari, anche f+g è dispari. Invece, la somma tra una funzione pari e una dispari non ha parità in generale. Queste proprietà aiutano ad aggregare modelli senza perdere simmetrie utili.
Per i prodotti: pari×pari → pari; dispari×dispari → pari; pari×dispari → dispari. Un esempio classico è cos(x)·sin(x): il prodotto tra una funzione pari e una dispari è dispari, e infatti h(x) = cos(x)·sin(x) rispetta h(−x) = −h(x).
Scalari: moltiplicare o dividere una funzione pari o dispari per un numero reale λ ≠ 0 preserva la parità. Al contrario, aggiungere o sottrarre uno scalare mantiene pari una funzione già pari (ad esempio x8 ± 5 resta pari), ma in genere rompe la parità dispari (poiché f(0) smette di essere zero).
Monomi: f(x) = xn è pari se n è pari (x2, x4, …) e dispari se n è dispari (x, x3, x5, …). Queste osservazioni costruiscono rapidamente famiglie di esempi con parità nota.
Perché la parità è utile in fisica e nell’ondulatoria
In analisi e fisica, la parità consente scorciatoie eleganti: integrando su un intervallo simmetrico , l’integrale di una funzione dispari vale 0, mentre quello di una funzione pari vale il doppio dell’integrale su . Questo è cruciale nello studio di onde e vibrazioni, nelle serie di Fourier (dove si separano componenti pari e dispari), e in problemi con condizioni al contorno simmetriche.
Nel dominio delle onde, sinusoidi come sin e cos presentano parità complementare e sono i mattoni delle oscillazioni; la distinzione tra componenti pari e dispari permette di semplificare analisi, scomposizioni e calcoli di fenomeni periodici e stazionari.
Classificazione delle onde: natura, dimensioni e vibrazione
Le onde sono perturbazioni che si propagano trasportando energia senza trasportare materia. Dal punto di vista della natura: le onde meccaniche richiedono un mezzo (percezione del suono, onde su corde o molle), le elettromagnetiche no (si propagano anche nel vuoto: luce, microonde, radio), e le gravitazionali sono increspature dello spazio-tempo generate da masse imponenti in dinamica (ad esempio buchi neri in collisione).
Per il numero di direzioni di propagazione: unidimensionali (una sola direzione, come un’onda su una corda), bidimensionali (propagazione su superfici, come increspature in uno specchio d’acqua), tridimensionali (si diffondono nello spazio, come suono e luce). Questa tassonomia aiuta a prevedere geometrie d’onda e attenuazioni.
Quanto alla direzione di vibrazione: onde longitudinali (oscillano nella stessa direzione di propagazione, come il suono) e trasversali (oscillano perpendicolarmente alla direzione di avanzamento, come le onde su una corda o la luce). La distinzione è fondamentale per fenomeni come polarizzazione, che riguarda solo onde trasversali.
Elementi e grandezze d’onda: λ, f, T, v e relazioni utili
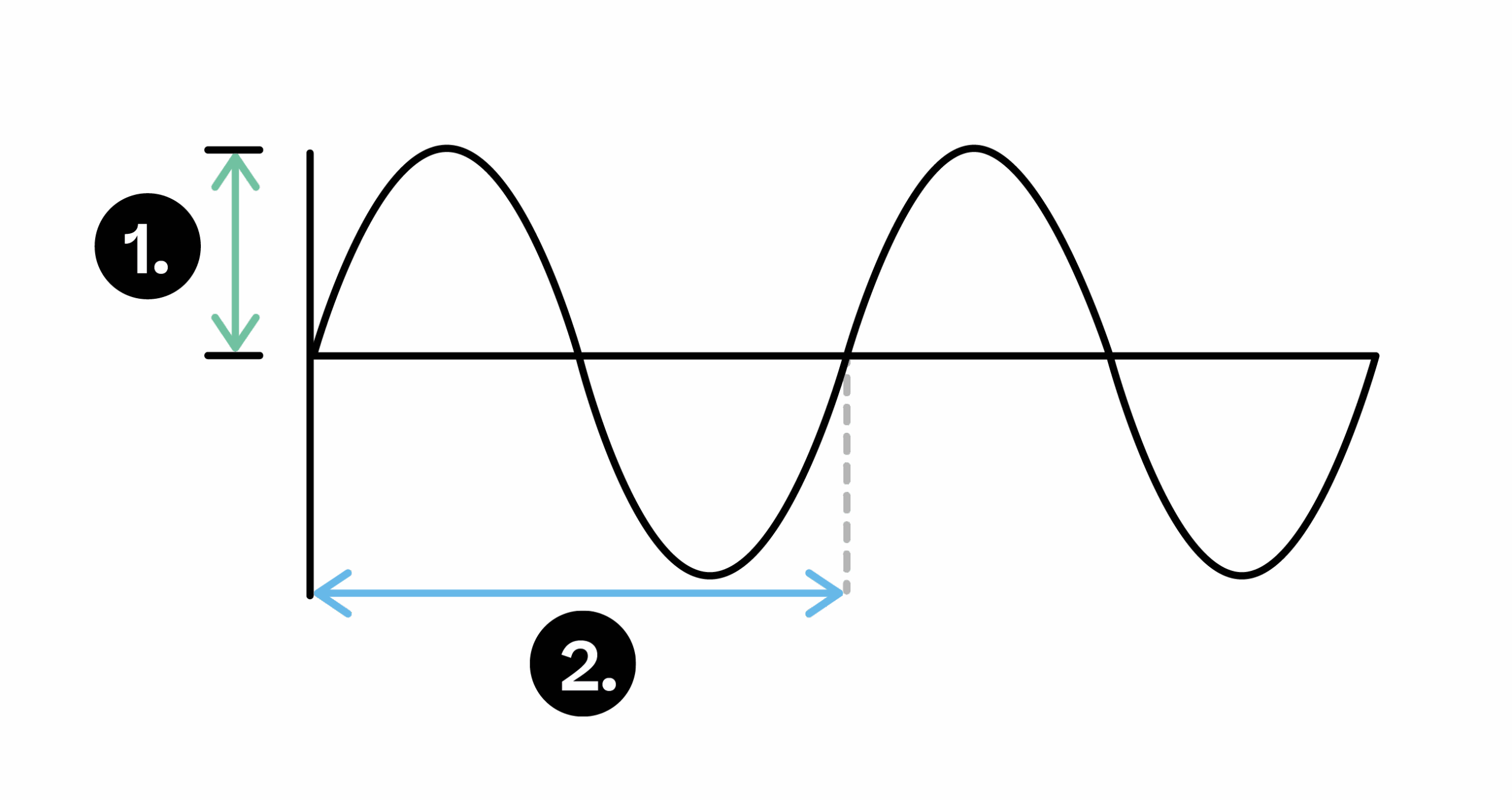
Ogni onda periodica presenta elementi ricorrenti: cresta (massimo), valle (minimo), ampiezza (scostamento massimo dal livello di equilibrio), lunghezza d’onda λ (distanza tra due punti equivalenti, ad es. cresta–cresta), periodo T (tempo di un’oscillazione) e frequenza f (oscillazioni per secondo). Le grandezze sono legate da v = λ·f e T = 1/f, dove v è la velocità di propagazione.
Un esempio pratico: se una onda ha λ = 2 m e f = 100 Hz, allora v = λ·f = 2·100 = 200 m/s. Se la frequenza vale 200 Hz, il periodo è T = 1/f = 0,005 s. Queste relazioni sono cardini di esercizi e applicazioni.
Sulle corde tese, la velocità dipende da tensione e densità lineare μ: v = √(F/μ). Questa formula (nota anche come equazione di Taylor per le onde su corda ideale) mostra che aumentando la tensione la velocità cresce, mentre corde più “pesanti” (μ maggiore) la rallentano.
Onde stazionarie, corde vibranti e tubi sonori
Un’onda stazionaria nasce dalla sovrapposizione di due onde di pari frequenza che si muovono in versi opposti; compaiono nodi (ampiezza nulla) e ventri (ampiezza massima). In una corda fissata alle estremità, i modi di vibrazione sono discreti e ben definiti.
Per una corda di lunghezza L con estremità fisse, i modi normali hanno lunghezze d’onda λ = 2L/N e frequenze fN = N·v/(2L), con N = 1, 2, 3, …; il primo modo (fondamentale) ha λ = 2L e f = v/(2L). L’aggiunta di nodi/ventri genera modi superiori (armoniche) con frequenze multiple della fondamentale.
Nei tubi sonori, cambia la condizione al contorno: nel tubo aperto alle due estremità valgono formule analoghe alla corda (λ = 2L/N e fN = N·v/(2L)); in un tubo chiuso a un’estremità esistono solo armoniche di ordine dispari: λ = 4L/i e fi = i·v/(4L) con i = 1, 3, 5, … (ad esempio la fondamentale ha λ = 4L e f = v/(4L)). Questi schemi spiegano la diversa “tavolozza” di frequenze di strumenti a corda e a fiato.
Fenomeni ondulatori: riflessione, rifrazione, assorbimento, polarizzazione, dispersione, diffrazione, interferenza e risonanza
La riflessione si verifica quando un’onda incontra un ostacolo e “rimbalza” rimanendo nello stesso mezzo; è l’effetto che ci consente di vedere il riflesso in uno specchio o nell’acqua. Gli angoli rispetto alla normale rispettano la legge di uguaglianza incidenza = riflessione.
La rifrazione avviene quando l’onda entra in un altro mezzo, cambiando velocità e direzione (ma non la frequenza); per la luce, la legge di Snell è n1·sinθ1 = n2·sinθ2. È la ragione per cui oggetti immersi in acqua ci appaiono spostati rispetto alla posizione reale.
L’assorbimento descrive come un materiale trattiene parte dell’energia dell’onda (nel caso della luce, determina il colore percepito: un oggetto rosso assorbe le altre componenti e riflette il rosso). Questa interazione dipende sia dallo spettro della sorgente sia dalle proprietà del materiale.
La polarizzazione filtra le componenti di vibrazione delle onde trasversali; con i filtri polarizzatori possiamo attenuare riflessi indesiderati nelle fotografie selezionando una direzione di vibrazione preferita. La luce naturale è in genere non polarizzata, ma può essere parzialmente polarizzata per riflessione o diffusione.
La dispersione è la scomposizione della luce in componenti monocromatiche con velocità (e dunque indici) differenti: un prisma separa il bianco nei colori dello spettro. È un caso specifico di rifrazione in cui l’indice dipende dalla frequenza.
La diffrazione (principio di Huygens) è la capacità di un’onda di aggirare ostacoli o “allargarsi” dopo una fenditura: è grazie a questo effetto che il segnale Wi‑Fi può raggiungerci anche dietro muri e anfratti, specie se la lunghezza d’onda è comparabile con le dimensioni dell’apertura.
L’interferenza è la somma (sovrapposizione) di onde: può essere costruttiva (ampiezza maggiore) o distruttiva (si attenuano o annullano). L’esperimento delle doppie fenditure di Young illustra magnificamente queste figure a frange chiare e scure.
La risonanza si verifica quando una struttura è sollecitata a una frequenza vicina a una delle sue frequenze naturali: l’ampiezza cresce e può diventare pericolosa. Il caso storico del ponte di Tacoma Narrows mostra quanto l’accoppiamento tra vento e struttura possa innescare oscillazioni catastrofiche.
Formule essenziali di fisica: prontuario ragionato
Di seguito un riepilogo, con simboli standard e significati, delle formule più utilizzate nei corsi introduttivi. Ogni relazione è un mattoncino pratico per problemi d’esame o di laboratorio.
Cinematica
MRU: s = s0 + v·Δt. Qui s è la posizione finale, s0 l’iniziale, v la velocità costante, Δt l’intervallo di tempo; capire questi termini aiuta a modellare traslazioni uniformi.
MRUV: s = s0 + v0·t + (1/2)·a·t2; v = v0 + a·t; v2 = v02 + 2·a·Δs. Queste tre espressioni descrivono il moto uniformemente accelerato in tutte le sue varianti.
Moto circolare uniforme: v = ω·R, ac = v2/R e ω = 2π·f. Collegano velocità lineare, velocità angolare, raggio e frequenza.
Lancio obliquo: vx = v0·cosθ, v0y = v0·sinθ, vy = v0y + a·t. Proiettare il moto in componenti orizzontale e verticale rende i calcoli molto più semplici.
Dinamica
Seconda legge di Newton: FR = m·a. È la base del legame tra forza risultante e variazione di moto.
Peso: P = m·g; attrito: fat = μ·N; elasticità (molla): Fel = k·x. Queste relazioni modellano interazioni comuni tra corpo e ambiente.
Lavoro, energia e potenza
Lavoro: W = F·d·cosθ, energia cinetica Ec = (1/2)·m·v2, potenziale gravitazionale Ep = m·g·h, potenziale elastica Eel = (1/2)·k·x2. Questi mattoni energetici sono il cuore del principio di conservazione.
Potenza: P = W/Δt. Conoscere quanta energia per unità di tempo si scambia è cruciale per valutare prestazioni di macchine e dispositivi.
Quantità di moto e impulso
Quantità di moto: Q = m·v; impulso: I = F·Δt. Gli urti e le interazioni brevi si analizzano bene con queste grandezze, sfruttando conservazioni e bilanci.
Idrostatica
Pressione: p = F/A; densità: ρ = m/V; legge di Stevino: ptot = patm + ρ·g·h; spinta (Archimede): E = ρ·g·V. Sono essenziali per fluidi in equilibrio e galleggiamento.
Gravitazione
Keplero: T2 = K·r3; Newton: FG = G·M1·M2/d2. Queste formule descrivono orbite e interazioni a grande scala.
Termologia e termodinamica
Conversione Kelvin: TK = TC + 273; dilatazioni: ΔL = L0·α·ΔT, ΔA = A0·β·ΔT, ΔV = V0·γ·ΔT. Le dilatazioni modellano effetti di temperatura su solidi.
Calorimetria: C = m·c, Q = m·c·ΔT e Q = m·L (cambio di fase). Questi bilanci sono la chiave per scambi termici e transizioni.
Primo principio: ΔU = Q − W (segno di W come lavoro fatto dal sistema); per cicli termici, il lavoro netto W = Qcalda − Qfredda; l’entropia per trasformazioni reversibili si scrive ΔS = ΔQrev/T.
Onde e ottica
Velocità d’onda: v = λ·f (equivalentemente v = λ/T). È la relazione più usata in ondulatoria.
Specchi sferici: 1/f = 1/p + 1/p′, ingrandimento A = i/o = −p′/p. Conoscere segni e convenzioni consente di tracciare immagini reali o virtuali.
Rifrazione (Snell): n1·sinθ1 = n2·sinθ2. Al variare dell’indice cambia la direzione e la velocità dell’onda.
Elettricità
Coulomb: Fe = k·|Q1Q2|/d2, forza su carica di prova: F = q·E, potenziale V = k·Q/d. Sono i pilastri dei campi elettrici.
Ohm: U = R·i, potenza elettrica P = U·i = R·i2, energia elettrica E = P·Δt. Queste relazioni governano circuiti semplici.
Resistenze: in serie Req = R1 + R2 + …; in parallelo 1/Req = 1/R1 + 1/R2 + … . Capacità: C = Q/U. Questo trittico supporta analisi di reti elettriche.
Elettromagnetismo
Lorentz: Fm = B·|q|·v·sinθ (su carica in moto), e su un tratto percorso da corrente Fm = B·i·l·sinθ. Il flusso magnetico è φ = B·A·cosθ, mentre l’induzione elettromotrice segue Faraday‑Lenz: ε = −Δφ/Δt. Questi principi unificano elettricità e magnetismo nelle applicazioni moderne come la bobina di Tesla.
Esempi mirati: applicazioni rapide di parità e onde
Somma e prodotto: se f(x) = x2 (pari) e g(x) = 2x4 (pari), allora (f+g)(x) = x2 + 2x4 resta pari. Se invece f(x) = x3 e g(x) = 3x5 (entrambe dispari), la somma è dispari, mentre il prodotto è pari (dispari×dispari).
Prodotti misti: con f(x) = x2 (pari) e g(x) = x3 (dispari), otteniamo h(x) = x5 (dispari). Con funzioni trigonometriche, cos(x) è pari e sin(x) è dispari: h(x) = cos(x)·sin(x) è dispari. L’uso costante di queste regole riduce sforzi nel riconoscere simmetrie.
Interferenza: in un punto di sovrapposizione, l’effetto risultante è la somma algebrica dei contributi che le onde avrebbero prodotto individualmente. Dopo l’incontro, le onde riprendono il loro cammino con caratteristiche inalterate, un principio cruciale per comprendere frange e nodi.
Cordofoni e armoniche: per L dato, la fondamentale di una corda ha frequenza f = v/(2L); il secondo armonico raddoppia la frequenza (v/L), il terzo la triplica (3v/2L), e così via. Nei tubi chiusi, come visto, emergono solo armoniche dispari (v/4L, 3v/4L, 5v/4L…), decisivo per il timbro degli strumenti a fiato.
Esercizio tipico: un’onda sonora nel’aria viaggia a v = 340 m/s con λ = 5 m. Allora f = v/λ = 340/5 = 68 Hz. Questo calcolo si ripete in molti contesti (acustica, telecomunicazioni, vibrazioni meccaniche) con lo stesso schema.
Risonanza strutturale: eccitazioni periodiche (vento, macchine, onde) possono allinearsi con frequenze proprie e amplificare l’oscillazione. Il caso del ponte di Tacoma mostra che trascurare la risonanza può condurre a conseguenze gravi; il controllo delle frequenze naturali è quindi strategico in progettazione.
Suggerimenti pratici: parità, integrali e simmetria nei problemi
Quando un problema offre un dominio simmetrico e una funzione nota per essere pari o dispari, conviene “sfruttare” la parità prima di integrare o sommare: integrali di dispari su danno 0, mentre per le pari basta calcolare su e raddoppiare. In onde e segnali, decomporre una funzione in parte pari e dispari semplifica Fourier e molte condizioni al contorno.
Nella pratica numerica e nella modellazione, riconoscere immediatamente cos’è pari o dispari evita di “combattere” contro i termini che per simmetria si annullano. È un’abitudine che fa risparmiare tempo e riduce gli errori nei calcoli.
Sezione formule: controlli rapidi di coerenza dimensionale (ad esempio che un’energia sia in joule, una pressione in pascal) aiutano a individuare refusi e a mantenere affidabile il processo di soluzione. Anche ricordare che certi coefficienti (come 1/2 in energie) sono indispensabili è una buona pratica.
Per un ripasso “smart”, conviene tenere a portata di mano le relazioni v = λ·f, v = v0 + a·t, F = m·a, W = F·d·cosθ, Ec = (1/2)·m·v2, U = R·i, ε = −Δφ/Δt: coprono una fetta enorme di esercizi classici.
Con questa prospettiva, la parità non è un mero “dettaglio” teorico: diventa un grimaldello per sfruttare simmetrie, potare termini inutili e mettere a fuoco la “struttura nascosta” dei problemi di fisica, specie nei contesti ondulatori e nelle equazioni con condizioni simmetriche.
Dalla definizione di funzione pari e dispari alle regole algebriche, dalla classificazione delle onde alle formule cardine della fisica, fino ai fenomeni come interferenza o risonanza, si vede come simmetria e parità offrano una bussola potente: riconoscerle consente di leggere grafici e grandezze con più rapidità, prevedere esiti sperimentali e, soprattutto, semplificare i conti senza perdere rigore o completezza.