A função de injeção é um conceito matemático que descreve uma função que associa cada elemento de um conjunto de origem a um único elemento em um conjunto de destino. Em outras palavras, a função de injeção não permite que dois elementos distintos do conjunto de origem sejam associados ao mesmo elemento do conjunto de destino.
Essa propriedade é importante em diversas áreas da matemática e da computação, pois garante a unicidade das relações entre os elementos dos conjuntos. Uma função de injeção também é chamada de função injetora.
Um exemplo comum de função de injeção é a função f(x) = x^2, onde cada elemento do conjunto de origem é associado ao seu quadrado no conjunto de destino. Outro exemplo seria a função f(x) = 2x, onde cada elemento do conjunto de origem é associado ao dobro de seu valor no conjunto de destino.
As funções de injeção são fundamentais em diversos contextos, como na análise de dados, na criptografia e em algoritmos de compressão de informações. Elas garantem a integridade e a unicidade das relações entre os elementos dos conjuntos envolvidos.
Qual a finalidade do sistema de injeção de combustível nos veículos automotivos?
O sistema de injeção de combustível nos veículos automotivos tem a principal finalidade de fornecer a quantidade correta de combustível para a mistura ar-combustível no motor. Esse sistema é responsável por garantir que o motor funcione de forma eficiente, com bom desempenho e baixas emissões de poluentes.
A injeção de combustível substituiu os antigos carburadores nos veículos modernos, proporcionando uma melhor precisão na entrega de combustível. Existem diferentes tipos de sistemas de injeção, como a injeção direta e a injeção indireta, cada um com suas particularidades e benefícios.
Além de fornecer a quantidade correta de combustível, o sistema de injeção de combustível também é responsável por ajustar a mistura ar-combustível de acordo com as condições de operação do motor, como a aceleração, a temperatura ambiente e a carga no veículo. Isso garante um funcionamento mais eficiente e econômico do motor.
Em resumo, a função do sistema de injeção de combustível nos veículos automotivos é garantir um funcionamento eficiente do motor, com bom desempenho, baixas emissões de poluentes e economia de combustível. É um componente essencial para o bom funcionamento do veículo e para a redução do impacto ambiental causado pela queima de combustíveis fósseis.
Exemplos de funções injetoras: o que são e como identificar.
As funções injetoras são aquelas em que cada elemento do domínio é associado a um único elemento do contradomínio. Em outras palavras, não há dois elementos diferentes no domínio que são mapeados para o mesmo elemento no contradomínio. Isso significa que não ocorre “colisão” de elementos, garantindo que a função seja unívoca.
Para identificar se uma função é injetora, é necessário verificar se elementos distintos do domínio são sempre mapeados para elementos distintos no contradomínio. Uma maneira de fazer isso é utilizando o teste da reta horizontal. Se ao desenhar retas horizontais e estas cortarem o gráfico da função em apenas um ponto, então a função é injetora.
Um exemplo de função injetora é a função f(x) = 2x. Se tomarmos dois valores diferentes para x, por exemplo x=1 e x=2, teremos f(1) = 2 e f(2) = 4, ou seja, cada valor de x é associado a um único valor de f(x).
Outro exemplo é a função g(x) = x². Neste caso, a função não é injetora, pois ao tomarmos x=1 e x=-1, teremos g(1) = 1 e g(-1) = 1, ou seja, dois valores diferentes de x são mapeados para o mesmo valor de g(x).
Qual a finalidade da injeção eletrônica nos motores automotivos?
A injeção eletrônica nos motores automotivos tem como principal finalidade controlar a quantidade de combustível injetada no motor, garantindo assim uma queima mais eficiente e reduzindo as emissões de poluentes. Além disso, a injeção eletrônica também é responsável por controlar a mistura ar/combustível, a ignição e outros parâmetros que influenciam no desempenho e na eficiência do motor.
Com a utilização da injeção eletrônica, é possível obter uma melhor performance do veículo, com uma resposta mais rápida do motor e uma economia de combustível mais eficiente. Isso ocorre porque o sistema é capaz de ajustar automaticamente a quantidade de combustível injetada de acordo com a demanda do motor, garantindo um funcionamento mais preciso e otimizado.
Em resumo, a injeção eletrônica nos motores automotivos é essencial para garantir um funcionamento adequado do veículo, proporcionando maior eficiência, redução de emissões e melhor desempenho. Por isso, é fundamental manter o sistema de injeção eletrônica sempre em bom estado de funcionamento, realizando as manutenções preventivas necessárias.
Entenda o funcionamento do serviço de injeção e sua importância para veículos automotivos.
A função de injeção em veículos automotivos é essencial para o seu bom funcionamento. A injeção consiste na introdução controlada de combustível no motor, garantindo a mistura correta de ar e combustível para a combustão interna.
Esse sistema trabalha em conjunto com outros componentes do veículo, como a bomba de combustível e o sensor de oxigênio, para garantir um desempenho eficiente e econômico. A injeção eletrônica, por exemplo, é responsável por monitorar constantemente as condições do motor e ajustar a quantidade de combustível injetada conforme necessário.
Alguns exemplos de sistemas de injeção utilizados em veículos automotivos são a injeção direta e a injeção multiponto. A injeção direta injeta o combustível diretamente na câmara de combustão, enquanto a injeção multiponto injeta o combustível nos dutos de admissão.
Em resumo, a injeção é uma peça fundamental no funcionamento dos veículos automotivos, garantindo um desempenho otimizado, uma maior economia de combustível e uma redução nas emissões de poluentes.
Função de injeção: o que é, para que serve e exemplos
Uma função injetiva é qualquer relação de elementos do domínio com um único elemento do codomain. Também conhecida como função de 1-1 ( 1-1 ), que são parte das funções de classificação no que diz respeito à forma como os seus elementos são relacionados.
Um elemento do codomain pode ser apenas uma imagem de um único elemento do domínio; dessa forma, os valores da variável dependente não podem ser repetidos.
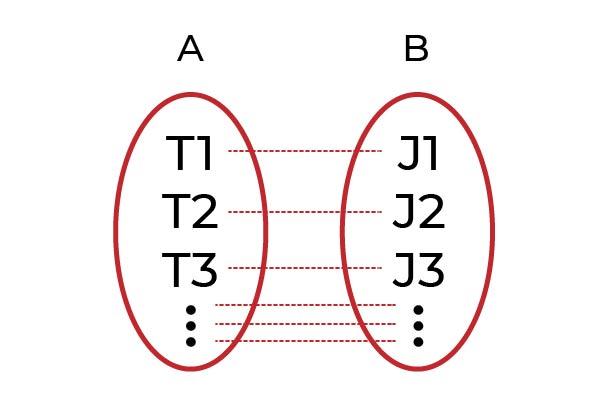
Um exemplo claro seria agrupar os homens com trabalho no grupo A e no grupo B todos os chefes. A função F será a que associa cada trabalhador ao seu chefe. Se cada trabalhador estiver associado a um chefe diferente por meio de F , F será uma função injetiva .
Para considerar uma função injetiva , o seguinte deve ser cumprido:
∀ x 1 ≠ x 2 ⇒ F (x 1 ) ≠ F (x 2 )
Esta é a maneira algébrica de dizer: Para cada x 1 diferente de x 2, você tem um F (x 1 ) diferente de F (x 2 ).
Para que servem as funções injetáveis?
A injetividade é uma propriedade das funções contínuas, pois elas garantem a atribuição de imagens para cada elemento do domínio, um aspecto essencial na continuidade de uma função.
Ao desenhar uma linha paralela ao eixo X no gráfico de uma função injetiva, o gráfico deve ser tocado apenas em um único ponto, independentemente da altura ou magnitude de Y em que a linha é desenhada. Esta é a maneira gráfica de testar a injetividade de uma função.
Outra maneira de testar se uma função é injetiva é limpar a variável independente X em termos da variável dependente Y. Em seguida, deve-se verificar se o domínio dessa nova expressão contém os números reais, ao mesmo tempo que para cada valor de Y existe apenas um valor de X.
As funções ou relações de ordem obedecem, entre outras formas, à notação F: D f → C f
O que é lido F que vai de D f a C f
Onde a função F relaciona os conjuntos Domínio e Codomain. Também conhecido como partida e chegada.
O domínio D f contém os valores permitidos para a variável independente. O codomain C f é composto por todos os valores disponíveis para a variável dependente. Os elementos de C f relacionados a D f são conhecidos como Intervalo de funções (R f ).
Função Condicionamento
Às vezes, uma função que não é injetável pode sofrer certas condições. Essas novas condições podem transformá-lo em uma função injetiva. Todos os tipos de modificações no domínio e co-domínio da função são válidos, onde o objetivo é cumprir as propriedades da injetividade no relacionamento correspondente.
Exemplos de funções injetáveis com exercícios resolvidos
Exemplo 1
Seja a função F: R → R definida pela linha F (x) = 2x – 3
A: [todos os números reais]
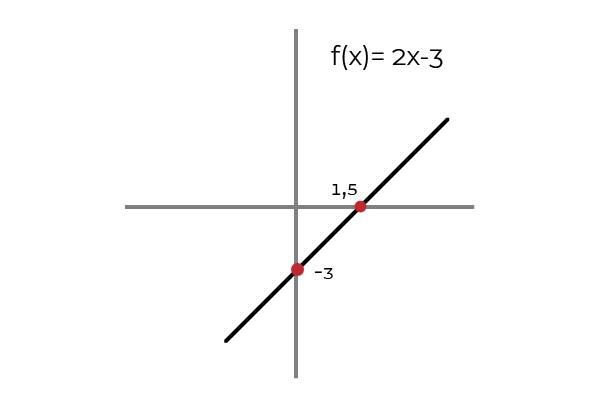
Observa-se que para cada valor de domínio há uma imagem no codomain. Essa imagem é única, o que faz de F uma função injetiva. Isso se aplica a todas as funções lineares (funções cujo maior grau de variável é um).
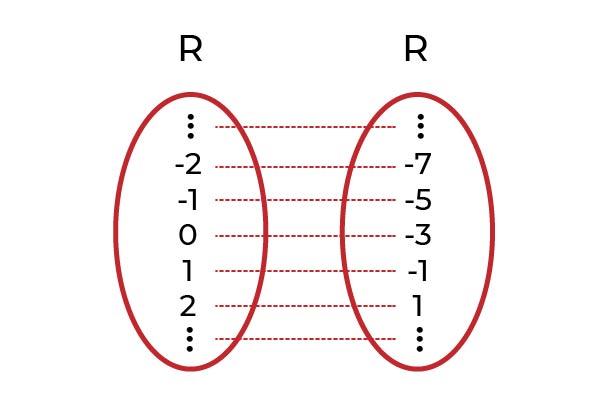
Exemplo 2
Seja a função F: R → R definida por F (x) = x 2 +1
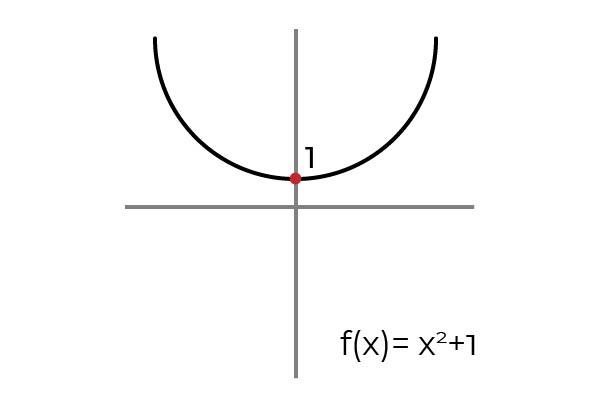
Ao desenhar uma linha horizontal, observa-se que o gráfico é encontrado em mais de uma ocasião. Por esse motivo, a função F não é injetiva enquanto R → R é definido
O domínio da função é condicionado:
F: R + U {0} → R

Agora a variável independente não assume valores negativos, evitando assim a repetição dos resultados e a função F: R + U {0} → R definida por F (x) = x 2 + 1 é injetiva .
Outra solução homóloga seria restringir o domínio à esquerda, ou seja, restringir a função a assumir apenas valores negativos e zero.
O domínio da função é condicionado
F: R – U {0} → R
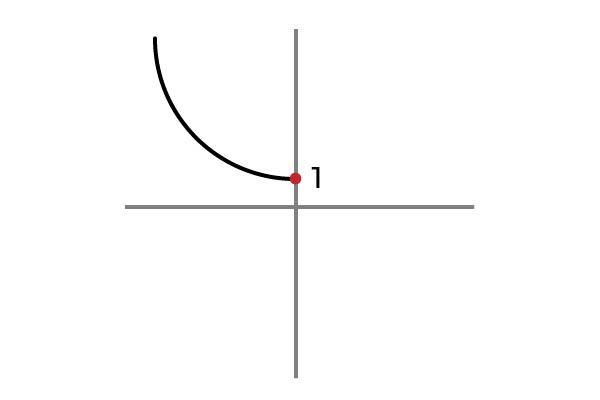
Agora a variável independente não assume valores negativos, evitando assim a repetição dos resultados e a função F: R – U {0} → R definida por F (x) = x 2 + 1 é injetiva .
Funções trigonométricas têm comportamentos parecidos com ondas, onde é muito comum encontrar repetições de valores na variável dependente. Através de condições específicas, baseadas no conhecimento prévio dessas funções, podemos restringir o domínio para atender às condições de injetividade.
Exemplo 3
Seja a função F: [- π / 2, π / 2 ] → R definido por F (x) = Cos (x)
No intervalo [- π / 2 → π / 2 ], a função cosseno varia seus resultados entre zero e um.
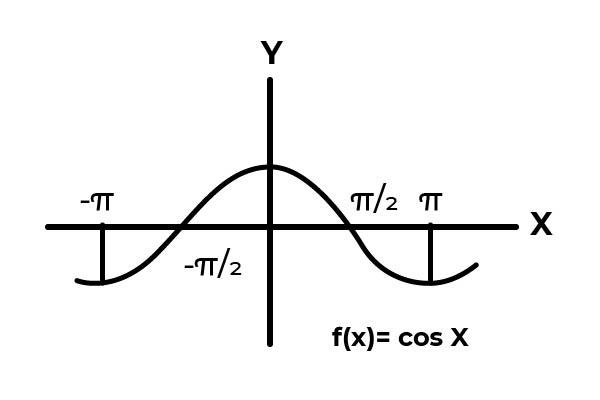
Como visto no gráfico. Comece do zero em x = – π / 2 e alcance o máximo em zero. É após x = 0 que os valores começam a se repetir, até que retornem a zero em x = π / 2. Dessa maneira, sabe-se que F (x) = Cos (x) não é injetivo para o intervalo [- π / 2, π / 2 ] .
Ao estudar o gráfico da função F (x) = Cos (x) , são observados intervalos em que o comportamento da curva é adaptado aos critérios de injetividade. Como por exemplo o intervalo
[0 , π ]
Onde a função varia os resultados de 1 a -1, sem repetir nenhum valor na variável dependente.
Desta forma, a função de função F: [0 , π ] → R definida por F (x) = Cos (x). É injetável
Existem funções não lineares onde ocorrem casos semelhantes. Para expressões de tipo racional, onde o denominador abriga pelo menos uma variável, existem restrições que impedem a injetividade do relacionamento.
Exemplo 4
Seja a função F: R → R definida por F (x) = 10 / x
A função é definida para todos os números reais, exceto {0} que tem uma indeterminação (não pode ser dividida por zero) .
Ao se aproximar de zero à esquerda, a variável dependente recebe valores negativos muito grandes e, imediatamente após zero, os valores da variável dependente recebem números positivos grandes.
Essa interrupção causa a expressão F: R → R definida por F (x) = 10 / x
Não seja injetável.
Como visto nos exemplos anteriores, a exclusão de valores no domínio serve para “reparar” essas indeterminações. Continuamos excluindo zero do domínio, deixando os conjuntos de partidas e chegadas definidos da seguinte maneira:
R – {0} → R
Onde R – {0} simboliza os reais, exceto um conjunto cujo único elemento é zero.
Dessa maneira, a expressão F: R – {0} → R definida por F (x) = 10 / x é injetiva.
Exemplo 5
Seja a função F: [0 , π ] → R definida por F (x) = Sen (x)
No intervalo [0 , π ] a função seno varia seus resultados entre zero e um.
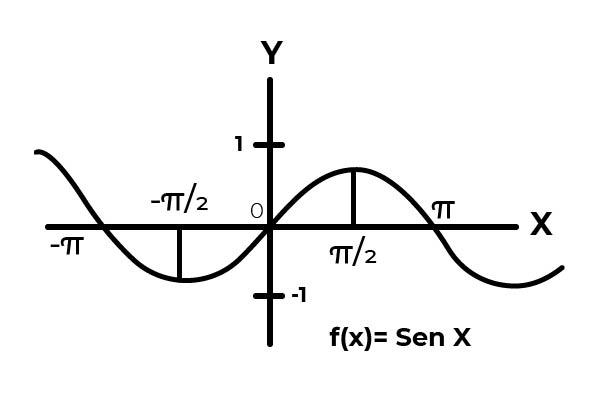
Como visto no gráfico. Comece do zero em x = 0 atingindo o máximo em x = π / 2. É após x = π / 2 que os valores começam a se repetir, até que retornem a zero em x = π. Dessa maneira, sabe-se que F (x) = Sen (x) não é injetivo para o intervalo [0 , π ] .
Ao estudar o gráfico da função , são observados intervalos F (x) = Sen (x) onde o comportamento da curva é adaptado aos critérios de injetividade. Como o intervalo [ π / 2 , 3π / 2 ]
Onde a função varia os resultados de 1 a -1, sem repetir nenhum valor na variável dependente.
Desta forma, a função F: [ π / 2 , 3π / 2 ] → R definida por F (x) = Sen (x). É injetável
Exemplo 6
Verifique se a função F: [0, ∞) → R definida por F (x) = 3x 2 é injetiva.
Nesta ocasião, o domínio da expressão já é limitado. Observa-se também que os valores da variável dependente não são repetidos neste intervalo.
Portanto, pode-se concluir que F: [0, ∞) → R definido por F (x) = 3x 2 é injetivo
Exemplo 7
Identifique qual das seguintes funções é
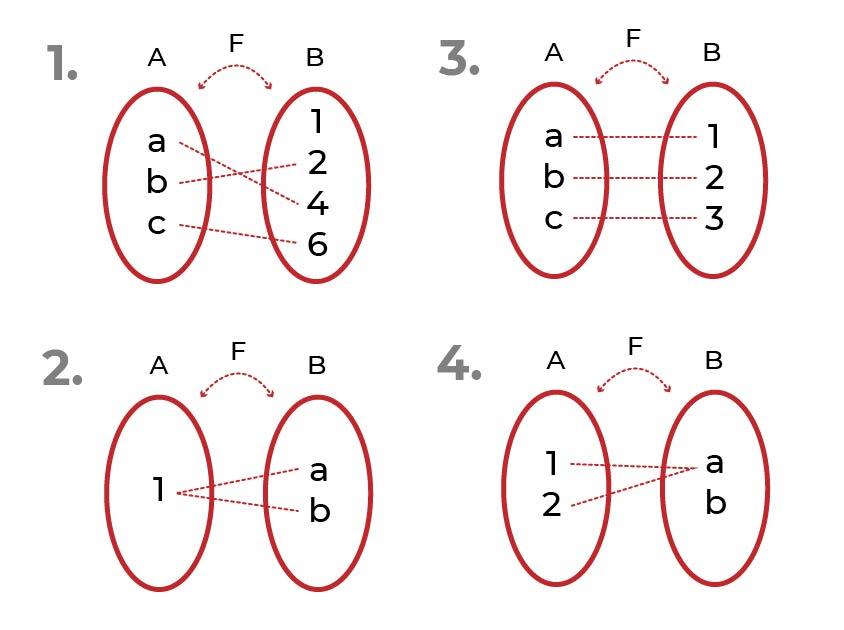
- É injetivo. Os elementos associados do codomain são exclusivos para cada valor da variável independente.
- Não é injetável. Existem elementos do codomain associados a mais de um elemento do conjunto inicial.
- É injetável
- Não é injetável
Exercícios propostos para a aula / casa
Verifique se as seguintes funções são injetivas:
F: [0, ∞) → R definido por F (x) = (x + 3) 2
F: [ π / 2 , 3π / 2 ] → R definido por F (x) = Tan (x)
F: [- π , π ] → R definido por F (x) = Cos (x + 1)
F: R → R definido pela linha F (x) = 7x + 2
Referências
- Introdução ao pensamento lógico e crítico. Merrilee H. Salmon. Universidade de Pittsburgh
- Problemas em Análise Matemática. Piotr Biler, Alfred Witkowski. Universidade de Wroclaw. Polônia
- Elementos de análise abstrata. Médico O’Searcoid PhD. Departamento de Matemática. Faculdade universitária de Dublin, Beldfield, Dublind 4.
- Introdução à Lógica e à Metodologia das Ciências Dedutivas. Alfred Tarski, Nova Iorque, Oxford. Imprensa da Universidade de Oxford.
- Princípios de análise matemática. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelona Espanha.