O gradiente potencial é uma grandeza vetorial que descreve a variação de um campo escalar em relação às direções do espaço. Ele é utilizado em diversas áreas da Física e da Matemática para representar a taxa de variação de um potencial em diferentes direções. O cálculo do gradiente potencial é feito através da derivada parcial do potencial em relação às coordenadas espaciais. Um exemplo comum de aplicação do gradiente potencial é na análise de campos de força, onde ele descreve a direção e intensidade da força resultante atuando sobre um objeto.
Como calcular o gradiente de forma simples e eficiente em poucos passos.
Para calcular o gradiente de forma simples e eficiente em poucos passos, é importante compreender que o gradiente representa a taxa de variação mais rápida de uma função escalar em um determinado ponto. Para isso, é necessário seguir os seguintes passos:
Passo 1: Identificar a função escalar pela qual deseja-se calcular o gradiente. Por exemplo, se temos a função f(x, y) = x^2 + y^2, essa será nossa função escalar.
Passo 2: Determinar as derivadas parciais da função em relação a cada uma de suas variáveis. No caso da função f(x, y) = x^2 + y^2, as derivadas parciais serão ∂f/∂x = 2x e ∂f/∂y = 2y.
Passo 3: Organizar as derivadas parciais em um vetor, resultando no gradiente da função. Para a função do exemplo, o gradiente será dado por ∇f = (2x, 2y).
Com esses passos simples, é possível calcular o gradiente de uma função de forma eficiente. Lembre-se de que o gradiente potencial é um conceito fundamental na análise matemática e pode ser aplicado em diversas áreas, como física e engenharia.
Significado e importância do gradiente de potencial total em sistemas físicos e geofísicos.
O gradiente de potencial total é uma grandeza importante em sistemas físicos e geofísicos, pois representa a variação do potencial em relação à distância. Ele indica a direção e intensidade com que o potencial varia em um determinado ponto, sendo crucial para entender o comportamento de campos de força em diferentes contextos.
No caso de sistemas físicos, o gradiente de potencial total é fundamental para determinar a direção em que uma partícula irá se mover sob a ação de uma força. Ele fornece informações essenciais para a análise de fenômenos como a condução de eletricidade em circuitos e o movimento de corpos em campos gravitacionais.
Já em sistemas geofísicos, o gradiente de potencial total é utilizado para estudar a distribuição de massas e densidades na Terra. Através da análise do gradiente, os geofísicos podem mapear as variações do campo gravitacional terrestre e obter informações sobre a estrutura interna do planeta.
Em resumo, o gradiente de potencial total desempenha um papel fundamental na compreensão e modelagem de sistemas físicos e geofísicos, permitindo a análise detalhada dos campos de força presentes nesses ambientes. Sua correta interpretação e cálculo são essenciais para o avanço do conhecimento em diversas áreas da ciência e tecnologia.
Entendendo o conceito de gradiente: o que é e como funciona na prática.
O gradiente potencial é um conceito matemático que descreve a variação de uma grandeza em relação a uma determinada direção. Ele é muito utilizado em diversas áreas, como física, engenharia e geografia, para analisar campos de força, potencial elétrico, entre outros fenômenos.
Para entender como o gradiente potencial funciona na prática, é importante compreender que ele representa a taxa de variação de uma função escalar em relação às suas coordenadas. Em outras palavras, ele indica a direção e a intensidade com que uma grandeza varia em um determinado ponto do espaço.
Para calcular o gradiente potencial de uma função, é necessário determinar as derivadas parciais em relação às coordenadas espaciais. Essas derivadas representam as taxas de variação da função em cada direção, o que permite determinar a direção de maior crescimento da função e a sua intensidade nessa direção.
Um exemplo prático de aplicação do gradiente potencial é na determinação do campo elétrico em um ponto específico. Ao calcular o gradiente do potencial elétrico em relação às coordenadas espaciais, é possível encontrar a direção e a intensidade do campo elétrico nesse ponto, o que é essencial para compreender o comportamento das cargas elétricas no espaço.
Entendendo o conceito de campo gradiente e sua importância na física e matemática.
O campo gradiente é uma importante ferramenta em física e matemática que descreve a variação de uma grandeza escalar em relação à posição no espaço. Em outras palavras, ele representa a direção e a taxa de variação de uma função escalar em um determinado ponto. O gradiente é frequentemente utilizado para descrever o comportamento de campos de força, como o campo gravitacional ou elétrico.
Uma das principais características do gradiente é que ele aponta na direção de maior crescimento da função escalar, ou seja, na direção em que a função aumenta mais rapidamente. Isso é representado matematicamente pelo vetor gradiente, que é calculado a partir das derivadas parciais da função em relação às coordenadas espaciais.
Na prática, o campo gradiente é utilizado para determinar a direção em que uma partícula se moverá sob a influência de um campo de forças. Além disso, ele também é essencial para a resolução de problemas de otimização em matemática, como encontrar o máximo ou mínimo de uma função.
Um exemplo simples de aplicação do gradiente é o cálculo do potencial elétrico em um ponto no espaço. Neste caso, o gradiente do potencial elétrico fornece a direção e a intensidade do campo elétrico naquele ponto, permitindo assim a análise do comportamento das cargas elétricas.
Em resumo, o campo gradiente desempenha um papel fundamental na descrição e análise de fenômenos físicos e matemáticos, fornecendo informações valiosas sobre a variação de grandezas escalares em relação ao espaço. Sua compreensão é essencial para o avanço em diversas áreas do conhecimento, tornando-se uma ferramenta poderosa e versátil para cientistas e matemáticos.
Gradiente potencial: características, cálculo e exemplo
O gradiente de potencial é um vetor que representa a razão da mudança no potencial elétrico em relação à distância em cada eixo de um sistema de coordenadas cartesianas. Assim, o vetor gradiente de potencial indica a direção na qual a taxa de variação do potencial elétrico é maior, dependendo da distância.
Por sua vez, o módulo de gradiente de potencial reflete a taxa de variação da variação do potencial elétrico em uma direção específica. Se o valor disso for conhecido em cada ponto de uma região espacial, o campo elétrico poderá ser obtido a partir do gradiente de potencial.
O campo elétrico é definido como um vetor, que possui uma direção e magnitude específicas. Ao determinar a direção na qual o potencial elétrico diminui mais rapidamente – afastando-se do ponto de referência – e dividindo esse valor pela distância percorrida, é obtida a magnitude do campo elétrico.
Caracteristicas
O gradiente de potencial é um vetor delimitado por coordenadas espaciais específicas, que medem a razão de mudança entre o potencial elétrico e a distância percorrida por esse potencial.
As características mais destacadas do gradiente de potencial elétrico estão detalhadas abaixo:
1- O gradiente potencial é um vetor. Portanto, possui uma magnitude e direção específicas.
2- Como o gradiente de potencial é um vetor no espaço, possui magnitudes endereçadas nos eixos X (largura), Y (alto) e Z (profundidade), se o sistema de coordenadas cartesianas for tomado como referência.
3- Esse vetor é perpendicular à superfície equipotencial no ponto em que o potencial elétrico é avaliado.
4 – O vetor gradiente de potencial é direcionado para a direção da variação máxima da função de potencial elétrico em qualquer ponto.
5- O módulo de gradiente de potencial é igual ao derivado da função de potencial elétrico em relação à distância percorrida na direção de cada um dos eixos do sistema de coordenadas cartesianas.
6- O gradiente de potencial tem valor zero em pontos estacionários (máximo, mínimo e pontos de cadeira).
7- No sistema internacional de unidades (SI), as unidades de medida do gradiente de potencial são volts / metros.
8- A direção do campo elétrico é a mesma em que o potencial elétrico diminui sua magnitude mais rapidamente. Por sua vez, o gradiente de potencial aponta na direção em que o potencial aumenta seu valor em relação a uma mudança de posição. Então, o campo elétrico tem o mesmo valor do gradiente de potencial, mas com o sinal oposto.
Como calcular?
A diferença no potencial elétrico entre dois pontos (ponto 1 e ponto 2) é dada pela seguinte expressão:
Onde:
V1: potencial elétrico no ponto 1.
V2: potencial elétrico no ponto 2.
E: magnitude do campo elétrico.
Angle: angular a inclinação do vetor do campo elétrico medido em relação ao sistema de coordenadas.
Expressando diferencialmente a referida fórmula, deduz-se o seguinte:
O fator E * cos (Ѳ) refere-se ao módulo do componente do campo elétrico na direção de dl. Seja L o eixo horizontal do plano de referência, então cos (Ѳ) = 1, assim:
A seguir, a razão entre a variação do potencial elétrico (dV) e a variação na distância percorrida (ds) é o módulo do gradiente de potencial para o referido componente.
Conclui-se que a magnitude do gradiente de potencial elétrico é igual ao componente do campo elétrico na direção do estudo, mas com o sinal oposto.
No entanto, como o ambiente real é tridimensional, o gradiente de potencial em um determinado ponto deve ser expresso como a soma de três componentes espaciais nos eixos X, Y e Z do sistema cartesiano.
Ao dividir o vetor do campo elétrico em seus três componentes retangulares, você tem o seguinte:
Se houver uma região no plano em que o potencial elétrico tenha o mesmo valor, a derivada parcial desse parâmetro em relação a cada uma das coordenadas cartesianas será nula.
Assim, em pontos que estão em superfícies equipotenciais, a intensidade do campo elétrico terá magnitude zero.
Finalmente, o vetor gradiente de potencial pode ser definido exatamente como o mesmo vetor de campo elétrico (em magnitude), com o sinal oposto. Assim, você tem o seguinte:
Exemplo
A partir dos cálculos anteriores, você deve:
No entanto, antes de determinar o campo elétrico com base no gradiente de potencial, ou vice-versa, primeiro determine a direção na qual a diferença de potencial elétrico aumenta.
Depois disso, é determinada a razão entre a variação do potencial elétrico e a variação da distância líquida percorrida.
Dessa maneira, é obtida a magnitude do campo elétrico associado, que é igual à magnitude do gradiente de potencial nessa coordenada.
Exercício
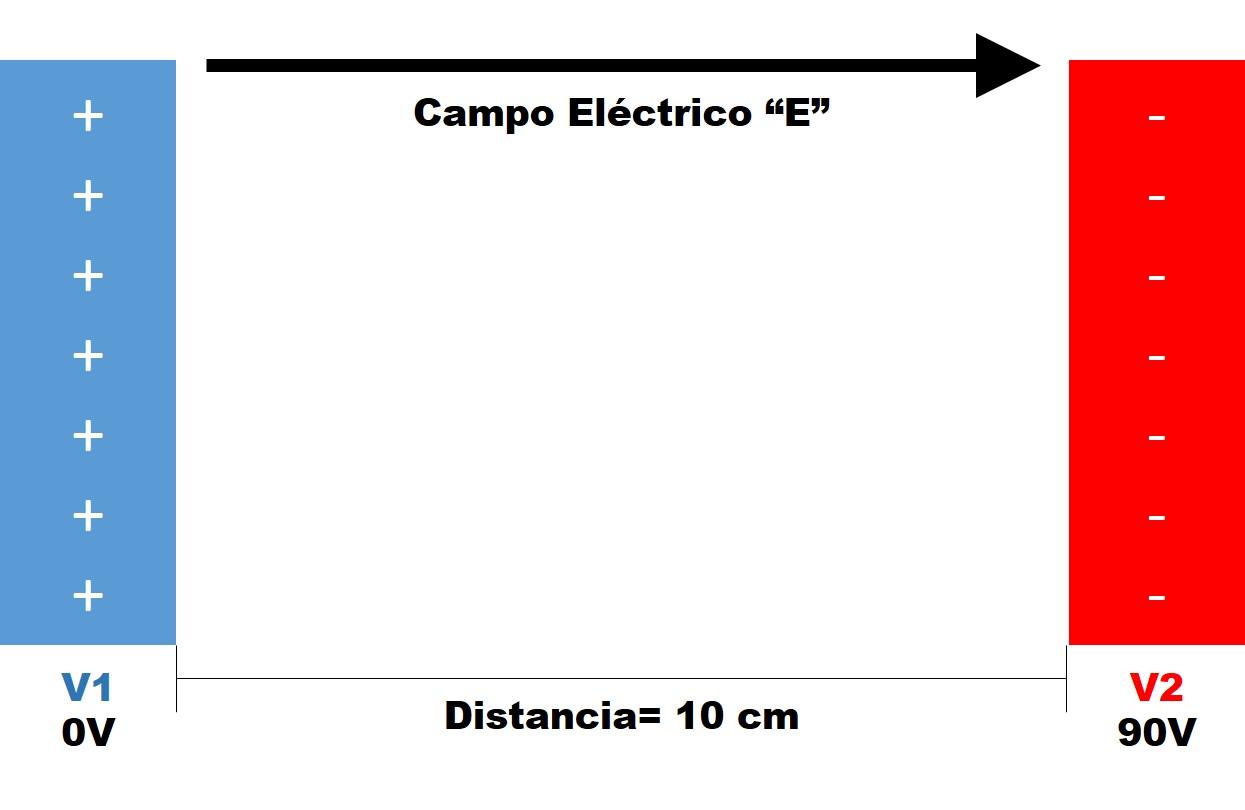
Existem duas placas paralelas, conforme refletido na figura a seguir.
Passo 1
A direção do crescimento do campo elétrico no sistema de coordenadas cartesianas é determinada.
O campo elétrico cresce apenas na direção horizontal, dada a disposição das placas paralelas. Consequentemente, é possível deduzir que os componentes do gradiente de potencial no eixo Y e no eixo Z são nulos.
Etapa 2
Os dados de interesse são discriminados.
– Diferença de potencial: dV = V2 – V1 = 90 V – 0 V => dV = 90 V.
– Diferença na distância: dx = 10 centímetros.
Para garantir a congruência das unidades de medida usadas de acordo com o Sistema Internacional de Unidades, as quantidades que não são expressas em SI devem ser convertidas em conformidade. Assim, 10 centímetros é igual a 0,1 metro e, finalmente: dx = 0,1 m.
Etapa 3
A magnitude do vetor gradiente potencial é calculada conforme apropriado.
Referências
- Eletricidade (1998). Encyclopædia Britannica, Inc. Londres, Reino Unido. Recuperado de: britannica.com
- Gradiente potencial (sf). Universidade Nacional Autônoma do México. Cidade do México, México. Recuperado de: professors.dcb.unam.mx
- Interação elétrica. Recuperado de: matematicasypoesia.com.es
- Gradiente potencial (sf). Recuperado de: circuitglobe.com
- Relação entre o potencial e o campo elétrico (sf). Instituto Tecnológico da Costa Rica. Cartago, Costa Rica. Recuperado de: repositoriotec.tec.ac.cr
- Wikipedia, A Enciclopédia Livre (2018). Gradiente Recuperado de: en.wikipedia.org