A indução magnética é um fenômeno físico que descreve a capacidade de um campo magnético em gerar uma força sobre uma partícula carregada em movimento. Essa grandezza é representada pela letra B e é medida em teslas (T). As fórmulas para calcular a indução magnética variam de acordo com a situação, podendo ser calculada a partir da força magnética, da corrente elétrica e do comprimento do fio condutor, por exemplo.
Neste contexto, a indução magnética pode ser calculada utilizando a fórmula B = F / (q * v * senθ), onde F representa a força magnética, q a carga da partícula, v sua velocidade e θ o ângulo entre a direção da velocidade e a direção do campo magnético.
Para exemplificar, podemos citar o caso de um fio condutor retilíneo percorrido por uma corrente elétrica. Nesse caso, a indução magnética pode ser calculada utilizando a fórmula B = (μ * I) / (2π * r), onde μ é a permeabilidade magnética do meio, I a corrente elétrica que percorre o fio e r a distância do ponto ao fio.
Assim, a indução magnética é uma grandeza fundamental para compreender o comportamento dos campos magnéticos e sua interação com partículas carregadas, sendo essencial para diversas aplicações práticas em áreas como a eletrônica, a física e a engenharia.
Cálculo da indução magnética: passo a passo para encontrar o valor correto.
Indução magnética é um conceito importante na física que descreve a força magnética em um determinado ponto do espaço. Para calcular a indução magnética, é necessário seguir alguns passos simples.
Primeiramente, é importante lembrar que a indução magnética é representada pela letra B e é medida em teslas (T). Para calcular a indução magnética em um determinado ponto, é necessário conhecer a força magnética e a área do campo magnético nesse ponto.
A fórmula para calcular a indução magnética é dada por:
B = F / A
Onde B é a indução magnética, F é a força magnética e A é a área do campo magnético. Para encontrar o valor correto da indução magnética, basta substituir os valores na fórmula e realizar o cálculo.
Por exemplo, se a força magnética em um determinado ponto é de 10 N e a área do campo magnético é de 5 m², podemos calcular a indução magnética da seguinte forma:
B = 10 / 5 = 2 T
Portanto, a indução magnética nesse ponto é de 2 teslas. Seguindo esses passos simples, é possível calcular a indução magnética corretamente em diferentes situações.
Conheça as diferentes maneiras de realizar a indução em processos e experimentos científicos.
A indução magnética é um fenômeno importante na física que descreve a geração de correntes elétricas em um condutor devido à variação de um campo magnético. Existem várias maneiras de realizar a indução em processos e experimentos científicos, cada uma com suas próprias características e aplicações.
Uma das formas mais comuns de realizar a indução magnética é por meio da lei de Faraday, que afirma que a força eletromotriz induzida em um circuito é igual à taxa de variação do fluxo magnético que atravessa a área do circuito. Essa relação é descrita pela fórmula:
EMF = -dΦ/dt
Onde EMF é a força eletromotriz induzida, dΦ é a variação do fluxo magnético e dt é o intervalo de tempo considerado. Essa fórmula é fundamental para calcular a indução magnética em diversos experimentos e aplicações.
Um exemplo prático de indução magnética é o funcionamento de um gerador elétrico, onde a rotação de um ímã próximo a um enrolamento de fios gera uma corrente elétrica. Esse processo é amplamente utilizado na geração de energia elétrica em usinas eólicas, por exemplo.
Outra maneira de realizar a indução magnética é por meio da lei de Lenz, que estabelece que a corrente induzida em um circuito sempre terá sentido oposto à variação do campo magnético que a gerou. Essa lei é essencial para compreender o comportamento dos sistemas sujeitos à indução magnética.
Em resumo, a indução magnética é um fenômeno complexo e fundamental na física, que pode ser estudado e aplicado de diversas maneiras em processos e experimentos científicos. Compreender as fórmulas e princípios envolvidos nesse fenômeno é essencial para explorar todo o seu potencial em diferentes áreas da ciência e da tecnologia.
Explicação da indução magnética: entenda como funciona esse fenômeno e suas aplicações práticas.
A indução magnética é um fenômeno que ocorre quando um campo magnético é gerado por meio do movimento de cargas elétricas. Esse campo magnético é capaz de gerar forças magnéticas que podem influenciar materiais magnéticos e elétricos, sendo de extrema importância em diversas aplicações práticas.
Para calcular a indução magnética em um determinado ponto, utilizamos a fórmula:
B = μ * H
Onde B representa a indução magnética, μ é a permeabilidade magnética do meio e H é a intensidade do campo magnético. Essa fórmula nos permite determinar a força do campo magnético em uma determinada região.
Um exemplo de aplicação prática da indução magnética é a utilização de transformadores, onde a variação do campo magnético é essencial para a transferência de energia entre bobinas. Além disso, a indução magnética é fundamental em equipamentos eletrônicos, motores elétricos e até mesmo em exames de ressonância magnética.
Portanto, compreender como a indução magnética funciona e saber como calcular sua intensidade é essencial para o desenvolvimento de tecnologias e aprimoramento de processos industriais.
Como calcular o campo magnético de um ímã ou solenoide?
Para calcular o campo magnético de um ímã ou solenoide, é necessário utilizar as fórmulas da indução magnética. A indução magnética é a propriedade que descreve a forma como um campo magnético é gerado por um ímã ou solenoide. Para calcular essa grandeza, é preciso levar em consideração a intensidade do campo magnético e a distância entre o ímã ou solenoide e o ponto de interesse.
Uma das fórmulas mais utilizadas para calcular o campo magnético é a lei de Ampère, que relaciona a intensidade do campo magnético (B) com a corrente elétrica que percorre o solenoide. A fórmula é representada por: B = μ0 * n * I, onde μ0 é a permeabilidade magnética do vácuo, n é o número de espiras por unidade de comprimento e I é a corrente elétrica que percorre o solenoide.
Outra fórmula importante é a lei de Biot-Savart, que descreve o campo magnético gerado por uma corrente elétrica em um ponto específico. A fórmula é dada por: B = (μ0 * I) / (2π * r), onde μ0 é a permeabilidade magnética do vácuo, I é a corrente elétrica e r é a distância entre o ponto e o condutor que gera o campo magnético.
Para exemplificar o cálculo do campo magnético de um solenoide, suponhamos que um solenoide de 100 espiras por metro e com uma corrente elétrica de 2 A gere um campo magnético a uma distância de 0,05 metros. Utilizando a fórmula B = μ0 * n * I, podemos calcular o campo magnético:
B = μ0 * 100 * 2 = 4π x 10^-7 * 100 * 2 = 8π x 10^-6 T
Portanto, o campo magnético gerado pelo solenoide a uma distância de 0,05 metros é de 8π x 10^-6 Tesla.
Indução magnética: fórmulas, como é calculada e exemplos
A indução magnética ou densidade de fluxo magnético é uma alteração do meio ambiente causados pela presença de correntes eléctricas. Eles modificam a natureza do espaço circundante, criando um campo vetorial.
O vetor de indução magnética, densidade de fluxo magnético ou simplesmente campo magnético B, tem três características distintivas: uma intensidade expressa por um valor numérico, uma direção e também uma direção dada em cada ponto do espaço. É destacado em negrito para diferenciá-lo de quantidades puramente numéricas ou escalares.

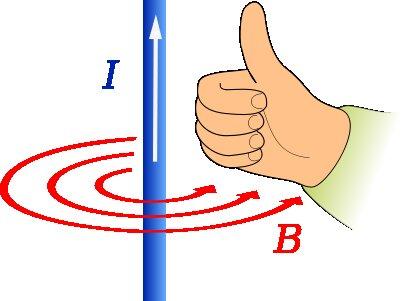
A régua de polegar direita é usada para encontrar a direção e a direção do campo magnético causada por um fio transportador de corrente, conforme mostrado na figura acima.
O polegar da mão direita deve apontar na direção da corrente. Então a rotação dos quatro dedos restantes indica a forma de B , que na figura é representada por círculos concêntricos de cor vermelha.
Nesse caso, a direção de B é tangencial à circunferência concêntrica com o fio e a direção é no sentido anti-horário.
A indução magnética B no Sistema Internacional é medida Tesla (T), porém é mais frequente medi-la em outra unidade chamada Gauss (G). Ambas as unidades foram nomeadas, respectivamente, em homenagem a Nikola Tesla (1856-1943) e Carl Friedrich Gauss (1777-1855) por suas extraordinárias contribuições à ciência da eletricidade e do magnetismo.
Quais são as propriedades da indução magnética ou densidade do fluxo magnético?
Um compasso é colocado perto da corrente de arame está sempre alinhada com B . O físico dinamarquês Hans Christian Oersted (1777-1851) foi o primeiro a perceber esse fenômeno no início do século XIX.
E quando a corrente cessa, a bússola aponta novamente para o norte geográfico, como sempre. Alterando cuidadosamente a posição da bússola, é obtido um mapa da forma do campo magnético.
Esse mapa sempre tem a forma de círculos concêntricos em relação ao fio, como descrito no início. Dessa forma, você pode exibir B.
Mesmo que o fio não seja reto, o vetor B formará círculos concêntricos ao redor dele. Para determinar qual a forma do campo, basta imaginar segmentos muito pequenos de arame, tão pequenos que parecem retilíneos e cercados por circunferências concêntricas.
Isso indica uma propriedade importante das linhas de campo magnético B : elas não têm começo nem fim, são sempre curvas acentuadas.
Lei de Biot-Savart
O século XIX determinou o início da era da eletricidade e do magnetismo na ciência. Circa 1820 físicos franceses Jean Marie Biot (1774-1862) e Felix Savart (1791-1841) descobriu a lei que leva seu nome e que calcula o vector B .
Eles fizeram as seguintes observações sobre a contribuição para o campo magnético produzido por um segmento de fio de comprimento diferencial dl que transporta uma corrente elétrica I :
- A magnitude de B diminui com o quadrado inverso da distância do fio (isso faz sentido: longe do fio, a intensidade de B deve ser menor do que em pontos próximos).
- A magnitude de B é proporcional à intensidade da corrente que passa através do fio.
- A direção de B é tangencial à circunferência do raio r centralizada no fio e a direção de B é dada, como dissemos, pela regra do polegar direito.
O produto vetorial ou produto cruzado é a ferramenta matemática apropriada para expressar o último ponto. São necessários dois vetores para estabelecer um produto vetorial, definido da seguinte forma:
- d l é o vetor cuja magnitude é o comprimento do segmento diferencial dl
- r é o vetor que vai do fio até o ponto em que você deseja encontrar o campo
Fórmulas
Tudo isso pode ser combinado em uma expressão matemática:
A constante de proporcionalidade necessária para estabelecer a igualdade é a permeabilidade magnética do espaço livre μ o = 4π.10 -7 Tm / A
Essa expressão é a lei de Biot e Savart, que permite calcular o campo magnético de um segmento atual.
Esse segmento, por sua vez, deve fazer parte de um circuito maior e mais fechado: uma distribuição de corrente.
A condição de fechamento do circuito é necessária para que a corrente elétrica flua. A corrente elétrica não pode fluir em circuitos abertos.
Finalmente, para encontrar o campo magnético total da referida distribuição de corrente, todas as contribuições de cada segmento diferencial dl são adicionadas . Isso equivale a integrar toda a distribuição:
Para aplicar a lei de Biot-Savart e calcular o vetor de indução magnética, é necessário considerar alguns pontos importantes muito importantes:
- O produto vetorial entre dois vetores sempre resulta em outro vetor.
- É conveniente encontrar o produto vetorial antes de passar para a resolução da integral, então a integral de cada um dos componentes obtidos separadamente é resolvida.
- É necessário desenhar uma imagem da situação e estabelecer um sistema de coordenadas apropriado.
- Sempre que a existência de qualquer simetria for observada, ela deve ser usada para economizar tempo de cálculo.
- Quando existem triângulos, o teorema de Pitágoras e o cosseno são de grande ajuda para estabelecer a relação geométrica entre as variáveis.
Como é calculado?
Com um exemplo prático do cálculo de B para um fio retilíneo, essas recomendações se aplicam.
Exemplo
Calcule o vetor do campo magnético que um fio retilíneo muito longo produz em um ponto P no espaço, de acordo com a figura mostrada.
A partir da figura, você deve:
- O fio é direcionado na direção vertical, com a corrente I fluindo para cima. Este endereço é + e no sistema de coordenadas, cuja origem está no ponto O.
- Nesse caso, de acordo com a regra do polegar direito , B no ponto P é direcionado para o papel, de modo que é indicado com um pequeno círculo e um “x” na figura. Este endereço será tomado como -z.
- O triângulo cujas pernas são e e R , ambas as variáveis relacionadas de acordo com o teorema de Pitágoras: r 2 = R 2 + y 2
Tudo isso é substituído na integral. O vetor ou produto cruzado é indicado por sua magnitude mais sua direção e seu significado:
A integral proposta é procurada em uma tabela de integrais ou é resolvida por uma substituição trigonométrica apropriada (o leitor pode verificar o resultado usando y = Rtg θ) :
O resultado é consistente com o esperado: a magnitude do campo diminui com a distância R e aumenta proporcionalmente com a intensidade da corrente I.
Embora um fio infinitamente longo seja uma idealização, a expressão obtida é uma aproximação muito boa para o campo de um fio longo.
Com a lei de Biot e Savart, é possível encontrar o campo magnético de outras distribuições de alta simetria, como um loop circular que transporta corrente ou fios dobrados combinando segmentos retilíneos e curvilíneos.
Obviamente, para resolver analiticamente a integral proposta, o problema deve ter um alto grau de simetria. Caso contrário, a alternativa é resolver numericamente a integral.
Referências
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 2 . México Cengage Learning Publishers. 367-372.



