As lentes convergentes são um tipo de lente que possui a capacidade de convergir os raios de luz em um único ponto, chamado de foco. Essas lentes são utilizadas em diversos dispositivos ópticos, como câmeras, microscópios e telescópios, devido às suas propriedades de focalização da luz.
Existem diferentes tipos de lentes convergentes, como as lentes biconvexas, plano-convexas e convexo-côncavas, cada uma com características específicas que influenciam a forma como os raios de luz são refratados ao atravessá-las.
Neste artigo, abordaremos as principais características das lentes convergentes, os diferentes tipos existentes e um exercício resolvido que ilustra como calcular a distância focal de uma lente convergente. Ao final, esperamos que o leitor tenha uma compreensão mais clara sobre esse importante componente óptico e suas aplicações.
Principais características de uma lente convergente: o que você precisa saber.
Uma lente convergente é um tipo de lente que possui a capacidade de direcionar os raios de luz que passam por ela para um ponto focal. Essas lentes são utilizadas em diversos dispositivos ópticos, como câmeras, microscópios e óculos de grau. Para entender melhor as características de uma lente convergente, é importante saber que elas possuem algumas propriedades específicas.
Uma das principais características de uma lente convergente é a sua capacidade de formar imagens reais ou virtuais, dependendo da posição do objeto em relação à lente. Quando o objeto está localizado além do ponto focal da lente, a imagem formada é real, invertida e menor do que o objeto. Por outro lado, quando o objeto está posicionado entre o ponto focal e a lente, a imagem formada é virtual, direita e maior do que o objeto.
Além disso, as lentes convergentes apresentam uma distância focal, que é a distância entre o ponto focal e o centro óptico da lente. Quanto menor for a distância focal, maior será a convergência dos raios de luz. Outra característica importante é o poder dióptrico da lente, que é a medida da capacidade da lente de convergir ou divergir os raios de luz. Lentes com poder dióptrico positivo são convergentes, enquanto lentes com poder dióptrico negativo são divergentes.
Existem diferentes tipos de lentes convergentes, como as lentes biconvexas, plano-convexas e convexo-côncavas, cada uma com suas próprias características e aplicações específicas. As lentes biconvexas são as mais comuns e são utilizadas em diversos equipamentos ópticos, como lupas e projetores. Já as lentes plano-convexas são utilizadas em sistemas de projeção e em microscópios. Por fim, as lentes convexo-côncavas são utilizadas em óculos corretivos para corrigir problemas de visão.
Para fixar o conhecimento sobre as características das lentes convergentes, vamos resolver um exercício simples: uma lente convergente possui uma distância focal de 10 cm. Se um objeto é colocado a 15 cm da lente, qual será a distância da imagem formada?
Exemplos de lentes convergentes: saiba mais sobre suas características e aplicações na óptica.
As lentes convergentes são um tipo de lente que possui a capacidade de direcionar os raios de luz para um ponto focal, onde ocorre a convergência. Essas lentes são utilizadas em diversos dispositivos ópticos, como câmeras, microscópios, telescópios e óculos de grau. Elas têm a capacidade de formar imagens reais e ampliadas, tornando-as muito úteis em diversas aplicações.
Existem diferentes tipos de lentes convergentes, sendo as mais comuns as lentes biconvexas, plano-convexas e côncavo-convexas. Cada tipo de lente convergente possui características específicas que determinam a forma como os raios de luz são refratados e focalizados. As lentes biconvexas, por exemplo, são espessas no centro e finas nas bordas, o que as torna ideais para a formação de imagens nítidas e ampliadas.
Um exemplo de aplicação das lentes convergentes é em microscópios, onde são utilizadas para ampliar a imagem de objetos pequenos. Outro exemplo é em câmeras fotográficas, onde as lentes convergentes são responsáveis por focalizar a luz que entra na câmera e formar a imagem capturada no sensor.
Para entender melhor como as lentes convergentes funcionam, vamos resolver um exercício simples. Suponha que tenhamos uma lente convergente com distância focal de 10 cm. Se um objeto está localizado a uma distância de 20 cm da lente, qual será a distância da imagem formada? Utilizando a equação de Gauss, podemos calcular que a imagem será formada a uma distância de 20 cm da lente, do lado oposto ao objeto.
Qual é o papel desempenhado pela lente convergente em um sistema óptico?
A lente convergente é um componente fundamental em um sistema óptico, desempenhando um papel crucial na formação de imagens. Ao contrário da lente divergente, que dispersa os raios de luz, a lente convergente é capaz de reunir os raios de luz em um único ponto, conhecido como ponto focal. Este processo é essencial para a formação de imagens nítidas e claras em diversos dispositivos ópticos, como câmeras, microscópios e telescópios.
As características principais de uma lente convergente incluem sua capacidade de convergir os raios de luz, sua espessura central maior que as extremidades e sua capacidade de formar imagens reais ou virtuais, dependendo da posição do objeto em relação à lente. Existem diferentes tipos de lentes convergentes, como as lentes biconvexas, plano-convexas e côncavo-convexas, cada uma com suas próprias propriedades e aplicações específicas.
Um exemplo de exercício envolvendo uma lente convergente seria o cálculo da distância focal da lente com base em sua curvatura e índice de refração do material. Para resolver esse exercício, é necessário aplicar as fórmulas adequadas e utilizar os conceitos de óptica geométrica para determinar a distância focal da lente.
Em resumo, a lente convergente desempenha um papel fundamental na formação de imagens em sistemas ópticos, reunindo os raios de luz em um ponto focal para produzir imagens nítidas e claras. Seu uso é essencial em uma variedade de dispositivos ópticos e seu estudo é de grande importância para compreender os princípios básicos da óptica.
Entenda o funcionamento das lentes convergentes e suas aplicações no dia a dia.
As lentes convergentes são um tipo de lente que possui a capacidade de convergir os raios de luz que passam por ela. Isso significa que essas lentes conseguem focalizar os raios de luz em um único ponto, conhecido como ponto focal. Esse fenômeno óptico é o que permite que as lentes convergentes sejam utilizadas em diversas aplicações no dia a dia.
Existem diversos tipos de lentes convergentes, sendo as mais comuns as lentes biconvexas e as lentes plano-convexas. As lentes biconvexas possuem as duas superfícies curvas, enquanto as lentes plano-convexas têm uma superfície plana e outra convexa. Independentemente do tipo, todas as lentes convergentes são capazes de formar imagens reais e invertidas.
No dia a dia, as lentes convergentes são amplamente utilizadas em diversos dispositivos ópticos, como câmeras fotográficas, óculos de grau e lupas. Nas câmeras fotográficas, por exemplo, as lentes convergentes são responsáveis por focalizar a luz que entra na câmera e formar a imagem no sensor ou filme fotográfico. Já nos óculos de grau, as lentes convergentes corrigem problemas de miopia e hipermetropia, permitindo que as pessoas enxerguem com mais nitidez.
Para entender melhor como as lentes convergentes funcionam, vamos resolver um exercício simples. Suponha que uma lente convergente tenha uma distância focal de 10 cm. Se um objeto está localizado a 20 cm da lente, qual será a posição da imagem formada pela lente? Utilizando a fórmula da lente fina, podemos calcular que a imagem será formada a 20 cm da lente, do lado oposto ao objeto, e será real e invertida.
Lente convergente: características, tipos e exercício resolvido
As lentes convergentes são aqueles que são mais espessas na sua parte central e mais fino nas extremidades. Como resultado, eles concentram (fazem convergir) em um único ponto os raios de luz que os atingem paralelamente ao eixo principal.Esse ponto é chamado de foco, ou foco de imagem, e é representado pela letra F. Lentes convergentes ou positivas formam o que é chamado de imagens reais de objetos.
Um exemplo típico de lente convergente é uma lupa. No entanto, é comum encontrar esse tipo de lente em dispositivos muito mais complexos, como microscópios ou telescópios. De fato, um microscópio composto básico consiste em duas lentes convergentes que possuem uma pequena distância focal. Essas lentes são chamadas objetivas e oculares.

As lentes convergentes são usadas em óptica para diferentes aplicações, embora talvez o mais conhecido seja o de corrigir defeitos de visão. Assim, eles são indicados para tratar hipermetropia, presbiopia e também alguns tipos de astigmatismo, como o astigmatismo hipermetrópico.
Caracteristicas
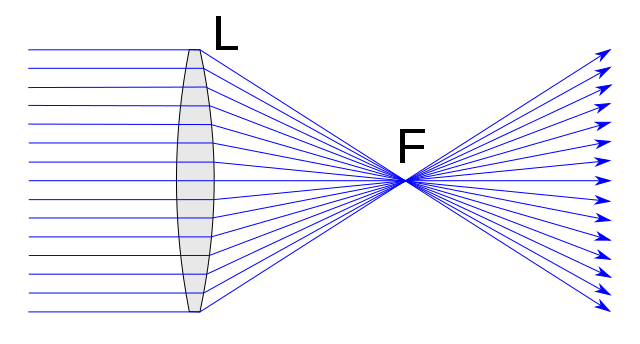
As lentes convergentes têm várias características definidoras. De qualquer forma, talvez o mais importante seja o que já avançamos em sua definição. Assim, as lentes convergentes são caracterizadas por desviar através do foco qualquer raio que as atinja em uma direção paralela ao eixo principal.
Além disso, reciprocamente, qualquer feixe incidente que passa pelo foco é refratado paralelamente ao eixo óptico da lente.
Elementos das lentes convergentes
Para o seu estudo, é importante saber quais elementos constituem as lentes em geral e as lentes convergentes em particular.
Em geral, é chamado o centro óptico de uma lente ao ponto em que todos os raios que passam por ela não sofrem nenhum desvio.
O eixo principal é a linha que une o centro óptico e o foco principal, que já mencionamos que é representado pela letra F.
O foco principal é chamado de ponto em que todos os raios que atingem a lente paralela ao eixo principal se encontram.
A distância entre o centro óptico e o foco é chamada de distância focal.
Os centros de curvatura são definidos como os centros das esferas que criam a lente; sendo, por outro lado, os raios de curvatura dos raios das esferas que dão origem à lente.
E, finalmente, o plano central da lente é chamado de plano óptico.
Formação de imagens em lentes convergentes
Para a formação de imagens em lentes convergentes, uma série de regras básicas explicadas abaixo deve ser levada em consideração.
Se o feixe atingir a lente paralelamente ao eixo, o feixe emergente convergirá para o foco da imagem. Por outro lado, se um feixe incidente cruza o foco do alvo, o feixe emerge em uma direção paralela ao eixo. Finalmente, os raios que cruzam o centro óptico são refratados sem sofrer nenhum tipo de desvio.
Como conseqüência, as seguintes situações podem ocorrer em uma lente convergente:
– Que o objeto esteja localizado em relação ao plano óptico a uma distância maior que o dobro da distância focal. Nesse caso, a imagem produzida é real, invertida e menor que o objeto.
– Que o objeto esteja localizado a uma distância do plano óptico igual ao dobro da distância focal. Quando isso acontece, a imagem obtida é uma imagem real, invertida e do mesmo tamanho que o objeto.
– Que o objeto esteja a uma distância do plano óptico entre uma e duas vezes a distância focal. Em seguida, uma imagem produzida é real, invertida e maior que o objeto original.
– Que o objeto esteja localizado a uma distância do plano óptico menor que a distância focal. Nesse caso, a imagem será virtual, direta e maior que o objeto.
Tipos de lentes convergentes
Existem três tipos diferentes de lentes convergentes: lentes biconvexas, lentes convexas planas e lentes convexas côncavas.
As lentes biconvexas, como o nome indica, consistem em duas superfícies convexas. Enquanto isso, os planos convexos têm uma superfície plana e convexa. E finalmente, as lentes côncavas-convexas são constituídas por uma superfície levemente côncava e convexa.
Diferença com lentes divergentes

As lentes divergentes, por outro lado, diferem das lentes convergentes, pois a espessura diminui das bordas em direção ao centro. Assim, ao contrário do que aconteceu com os convergentes, neste tipo de lente os raios de luz que atingem paralelamente ao eixo principal são separados. Dessa forma, eles formam o que é chamado de imagens virtuais de objetos.
Na óptica, as lentes divergentes ou negativas, como também são conhecidas, são usadas principalmente para corrigir a miopia.
Equações gaussianas de lentes finas e ampliação de uma lente
Em geral, o tipo de lente estudado é o tipo de lente fina. São definidos como aqueles que possuem uma espessura pequena em comparação com os raios de curvatura das superfícies que os limitam.
Este tipo de lente pode ser estudado com a equação gaussiana e com a equação que permite determinar a ampliação de uma lente.
Equação gaussiana
A equação gaussiana de lentes finas serve para resolver muitos problemas ópticos básicos. Daí a sua grande importância. Sua expressão é a seguinte:
1 / f = 1 / p + 1 / q
Onde 1 / f é o que é chamado de potência de uma lente ef é a distância focal ou distância do centro óptico ao foco F. A unidade de medida da potência de uma lente é a dioptria (D), onde 1 D = 1 m -1 . Por outro lado, pyq são respectivamente a distância em que um objeto está localizado e a distância em que sua imagem é observada.
Ampliando uma lente
A ampliação lateral de uma lente fina é obtida com a seguinte expressão:
M = – q / p
Onde M é o aumento. Do valor do aumento, uma série de consequências pode ser deduzida:
Sim | M | > 1, o tamanho da imagem é maior que o objeto
Sim | M | <1, o tamanho da imagem é menor que o do objeto
Se M> 0, a imagem está correta e no mesmo lado da lente que o objeto (imagem virtual)
Se M <0, a imagem é invertida e no lado oposto ao objeto (imagem real)
Exercício resolvido
Um corpo está localizado a um metro de distância de uma lente convergente, que tem uma distância focal de 0,5 metros. Como será a imagem corporal? Quão longe será?
Temos os seguintes dados: p = 1 m; f = 0,5 m.
Substituímos esses valores na equação gaussiana de lentes finas:
1 / f = 1 / p + 1 / q
E o seguinte permanece:
1 / 0,5 = 1 + 1 / q; 2 = 1 + 1 / q
Limpamos 1 / q
1 / q = 1
Para limpar e obter:
q = 1
Portanto, substituímos na equação de ampliação de uma lente:
M = – q / p = -1 / 1 = -1
Portanto, a imagem é real desde q> 0, invertida porque M <0 e de tamanho igual, já que o valor absoluto de M é 1. Finalmente, a imagem está a um metro de distância do foco.
Referências
- Luz (sd) Na WikipediaRetirado em 18 de março de 2019, de es.wikipedia.org.
- Lekner, John (1987).Teoria da reflexão, das ondas eletromagnéticas e de partículas . Springer
- Luz (sd). Na WikipediaRetirado em 20 de março de 2019, de en.wikipedia.org.
- Lente (nd). Na WikipediaRecuperado em 17 de março de 2019, de es.wikipedia.org.
- Lente (óptica) . Na WikipediaRecuperado em 19 de março de 2019, de en.wikipedia.org.
- Hecht, Eugene (2002).Optics (4ª ed.). Addison Wesley
- Tipler, Paul Allen (1994).Física 3ª edição . Barcelona: Eu inverti.