O modelo atômico de Sommerfeld foi proposto pelo físico alemão Arnold Sommerfeld em 1916 como uma extensão do modelo de Bohr. Este modelo apresenta algumas características importantes, como a consideração de órbitas elípticas para os elétrons em torno do núcleo, a introdução de números quânticos adicionais e a inclusão do spin dos elétrons.
Os postulados do modelo de Sommerfeld incluem a ideia de que os elétrons se movem em órbitas elípticas ao redor do núcleo, em vez de órbitas circulares, e que cada órbita pode conter um máximo de dois elétrons com spins opostos. Além disso, o modelo introduz os números quânticos azimutal e magnético, que descrevem as características das órbitas elípticas.
Uma das vantagens do modelo de Sommerfeld é a sua capacidade de explicar de forma mais precisa as energias dos elétrons em átomos com mais de um elétron, além de fornecer uma descrição mais completa do comportamento dos elétrons. No entanto, uma desvantagem do modelo é que ele ainda não consegue explicar completamente o comportamento dos átomos em situações mais complexas, como em átomos com muitos elétrons.
Postulados de Sommerfeld: Entenda os princípios fundamentais propostos pelo físico alemão.
O Modelo atômico de Sommerfeld foi proposto pelo físico alemão Arnold Sommerfeld no início do século XX. Este modelo apresentou algumas características inovadoras em relação aos modelos anteriores, como o Modelo de Bohr, e introduziu novos postulados que ajudaram a aprimorar a compreensão da estrutura dos átomos.
Um dos postulados principais de Sommerfeld foi a introdução das órbitas elípticas para descrever o movimento dos elétrons ao redor do núcleo. Além disso, ele propôs a ideia de que os elétrons podiam ocupar diferentes níveis de energia dentro dessas órbitas, chamados de subníveis.
Outro postulado importante foi a inclusão do spin dos elétrons, que é uma propriedade intrínseca das partículas subatômicas. Isso ajudou a explicar melhor a distribuição dos elétrons nos subníveis e a estabilidade dos átomos.
Uma das vantagens do Modelo atômico de Sommerfeld é a sua capacidade de descrever com mais precisão a estrutura dos átomos em comparação com os modelos anteriores. Além disso, ele permitiu prever com maior exatidão as propriedades químicas dos elementos.
No entanto, uma desvantagem do modelo de Sommerfeld é que ele ainda não era capaz de explicar completamente certos fenômenos observados experimentalmente, como a divisão de linhas espectrais em campos magnéticos.
Qual foi o principal legado deixado por Sommerfeld para a ciência da física?
O principal legado deixado por Sommerfeld para a ciência da física foi a sua contribuição significativa para o desenvolvimento do Modelo Atômico. Este modelo, proposto por ele em 1916, introduziu algumas características inovadoras que ajudaram a melhorar a compreensão da estrutura atômica.
Entre as características do Modelo Atômico de Sommerfeld, destacam-se a inclusão de órbitas elípticas para os elétrons ao redor do núcleo, em contraste com as órbitas circulares propostas por Bohr. Além disso, Sommerfeld introduziu os números quânticos adicionais, como o número azimutal, para descrever de forma mais precisa a distribuição dos elétrons.
Os postulados do Modelo Atômico de Sommerfeld proporcionaram uma melhor compreensão de fenômenos como a emissão e absorção de radiação eletromagnética pelos átomos. Isso contribuiu para avanços significativos na teoria quântica e na física atômica como um todo.
Apesar de suas vantagens, o Modelo Atômico de Sommerfeld também apresentava algumas desvantagens, como a complexidade matemática envolvida na descrição das órbitas elípticas dos elétrons. Além disso, o modelo não conseguia explicar completamente certos fenômenos observados em experimentos posteriores.
Apesar de suas limitações, o modelo de Sommerfeld foi fundamental para o progresso da física quântica e da física atômica.
Principais características do modelo atômico de Bohr: o que você precisa saber.
O modelo atômico de Bohr foi proposto por Niels Bohr em 1913 e introduziu várias características importantes para o entendimento da estrutura dos átomos. Uma das principais características é a ideia de que os elétrons orbitam o núcleo em órbitas circulares quantizadas, ou seja, apenas em determinados níveis de energia específicos. Além disso, Bohr postulou que os elétrons não emitem radiação enquanto estão em órbita estável, o que ajudou a explicar a estabilidade dos átomos.
Modelo atômico de Sommerfeld: características, postulados, vantagens e desvantagens
O modelo atômico de Sommerfeld, proposto por Arnold Sommerfeld em 1916, expandiu o modelo de Bohr ao introduzir órbitas elípticas e orbitais d e f para explicar melhor a complexidade dos átomos. Uma das principais vantagens desse modelo é a capacidade de descrever com mais precisão a estrutura dos átomos multieletrônicos, levando em consideração a forma das órbitas e a direção do momento angular dos elétrons.
No entanto, uma das desvantagens do modelo de Sommerfeld é que ele ainda não conseguia explicar completamente o espectro de emissão do hidrogênio, que era um dos principais desafios enfrentados pelos modelos atômicos da época. Apesar disso, o modelo de Sommerfeld foi um avanço significativo na compreensão da estrutura atômica e abriu caminho para desenvolvimentos futuros na área da física quântica.
Qual é o modelo atômico mais consagrado na atualidade?
O modelo atômico mais consagrado na atualidade é o Modelo Atômico de Sommerfeld. Esse modelo foi proposto pelo físico alemão Arnold Sommerfeld no início do século XX e trouxe importantes contribuições para a compreensão da estrutura do átomo.
Uma das principais características do Modelo Atômico de Sommerfeld é a consideração dos níveis de energia eletrônica em órbitas elípticas ao redor do núcleo atômico. Além disso, o modelo introduziu o conceito de números quânticos adicionais, como o número quântico azimutal, para descrever de forma mais precisa o comportamento dos elétrons dentro do átomo.
Os postulados do modelo de Sommerfeld incluem a ideia de que os elétrons se movem em órbitas elípticas ao redor do núcleo, com diferentes níveis de energia associados a cada órbita. Além disso, os elétrons podem ocupar órbitas com diferentes valores de momento angular, conforme descrito pelos números quânticos.
Uma das vantagens do Modelo Atômico de Sommerfeld é a sua capacidade de explicar de forma mais precisa as propriedades espectrais dos átomos, como as linhas de emissão e absorção. Além disso, o modelo permitiu um avanço significativo na compreensão da estrutura atômica e na predição de comportamentos observados experimentalmente.
No entanto, o Modelo Atômico de Sommerfeld também apresenta algumas desvantagens, como a complexidade matemática envolvida na descrição das órbitas elípticas e a dificuldade em visualizar essas órbitas de forma intuitiva. Além disso, o modelo não consegue explicar completamente fenômenos quânticos mais complexos, como a natureza dual partícula-onda dos elétrons.
Suas contribuições para a teoria quântica trouxeram avanços significativos no campo da física e da química, sendo amplamente estudado e utilizado até os dias de hoje.
Modelo atômico de Sommerfeld: características, postulados, vantagens e desvantagens
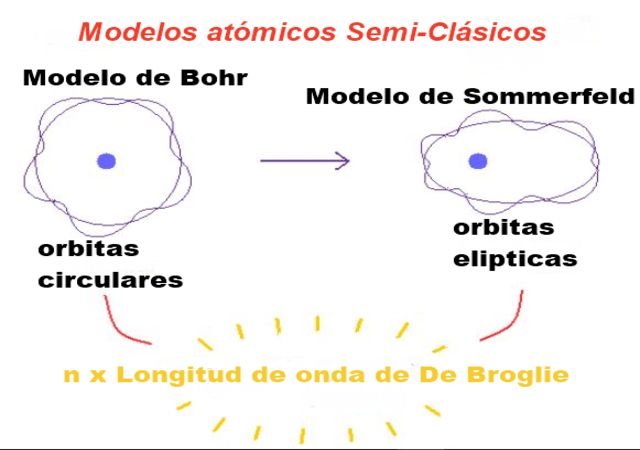
O modelo atômico Sommerfeld foi criado pelo físico alemão Arnold Sommerfeld entre 1915 e 1916, para explicar os fatos que o modelo Bohr, lançado no início de 1913, não conseguiu explicar satisfatoriamente. Sommerfeld apresentou seus resultados primeiro à Academia de Ciências da Baviera e depois os publicou na revista Annalen der Physik.
O modelo do átomo proposto pelo físico dinamarquês Niels Bohr descreve o átomo mais simples de todos, o do hidrogênio, mas não conseguiu explicar por que os elétrons no mesmo estado energético podem apresentar diferentes níveis de energia na presença de campos eletromagnéticos.
Na teoria de Bohr, o elétron que orbita o núcleo só pode ter certos valores de seu momento angular orbital L e, portanto, não pode estar em nenhuma órbita.
Bohr também considerou essas órbitas circulares e um único número quântico chamado número quântico principal n = 1, 2, 3 … serviu para identificar as órbitas permitidas.
A primeira modificação de Sommerfeld no modelo de Bohr foi assumir que a órbita eletrônica também pode ser elíptica.
Uma circunferência é descrita por seu raio, mas para uma elipse dois parâmetros devem ser dados: eixo semi-maior e eixo semi-menor, além de sua orientação espacial. Com isso, ele inseriu mais dois números quânticos.
A segunda grande modificação de Sommerfeld foi adicionar efeitos relativísticos ao modelo atômico. Nada é mais rápido que a luz; contudo, Sommerfeld havia encontrado elétrons com velocidades sensivelmente próximas; portanto, efeitos relativísticos tinham que ser incorporados a qualquer descrição do átomo.
O modelo atômico de Sommerfeld postula
Os elétrons seguem órbitas circulares e elípticas
Os elétrons no átomo seguem órbitas elípticas (órbitas circulares são um caso particular) e seu estado de energia pode ser caracterizado por três números quânticos: o número quântico principal n , o número quântico secundário ou número azimutal l e o número quântico magnético m L .
Diferentemente da circunferência, uma elipse tem um eixo semiorior e um semieixo menor.
Mas elipses com o mesmo eixo semi-maior podem ter diferentes semi-eixos menores, dependendo do grau de excentricidade. Uma excentricidade igual a 0 corresponde a uma circunferência, portanto, não descarta caminhos circulares. Além disso, no espaço as elipses podem ter inclinações diferentes.
Portanto Sommerfeld acrescentou a sua l secundário modelo número quântico para indicar o eixo menor e o quantum magnético número m L . Assim, ele apontou quais são as orientações espaciais permitidas da órbita elíptica.
Observe que ele não adiciona novos números quânticos principais; portanto, a energia total do elétron na órbita elíptica é a mesma que no modelo de Bohr. Portanto, não há novos níveis de energia, mas uma divisão dos níveis dados pelo número n.
Efeito Zeeman e efeito Stark
Dessa maneira, é possível especificar completamente uma determinada órbita, graças aos 3 números quânticos mencionados, e assim explicar a existência de dois efeitos: o efeito Zeeman e o efeito Stark.
E isso explica a divisão da energia que aparece no efeito Zeeman normal (também existe um efeito Zeeman anômalo), no qual uma linha espectral é dividida em vários componentes quando está na presença de um campo magnético.
Essa divisão das linhas também ocorre na presença de um campo elétrico, conhecido como efeito Stark, que levou Sommerfeld a pensar em modificar o modelo de Bohr para explicar esses efeitos.
O núcleo atômico e os elétrons se movem em torno de seu centro de massa
Depois que Ernest Rutherford descobriu o núcleo atômico, e também ficou claro que quase toda a massa do átomo está concentrada ali, os cientistas acreditavam que o núcleo era mais ou menos estacionário.
No entanto, Sommerfeld postulou que tanto o núcleo quanto os elétrons em órbita se movem ao redor do centro de massa do sistema, o que obviamente está muito próximo do núcleo. Seu modelo usa a massa reduzida do sistema elétron-núcleo, em vez da massa do elétron.
Nas órbitas elípticas, como nos planetas ao redor do Sol , há momentos em que o elétron está mais próximo e, às vezes, mais distante do núcleo. Portanto, sua velocidade é diferente em cada ponto de sua órbita.
Os elétrons podem atingir velocidades relativísticas
Sommerfeld introduziu a constante de estrutura fina, uma constante adimensional relacionada à força eletromagnética, em seu modelo:
α = 1 / 137.0359895
É definido como o quociente entre a carga do elétron e ao quadrado e o produto entre a constante de Planck he a velocidade da luz c no vácuo, todos multiplicados por 2π:
a = 2π (e 2 / hc) = 1 / 137,0359895
A constante de estrutura fina está relacionada a três das constantes mais importantes da física atômica. A outra é a massa do elétron, que não está listada aqui.
Dessa maneira, os elétrons estão ligados aos fótons (que se movem na velocidade c no vácuo) e, assim, explicam os desvios de algumas linhas espectrais do átomo de hidrogênio em relação àquelas previstas pelo modelo de Bohr.
Graças às correções relativísticas, os níveis de energia com n igual, mas diferente l são separados, dando origem à estrutura fina do espectro, daí o nome da constante α.
E todos os comprimentos característicos do átomo podem ser expressos em termos dessa constante.
Vantagens e desvantagens
Vantagem
-Sommerfeld mostrou que um único número quântico era insuficiente para explicar as linhas espectrais do átomo de hidrogênio.
Foi o primeiro modelo a propor uma quantização espacial, uma vez que as projeções das órbitas na direção do campo eletromagnético são, na verdade, quantizadas.
-O modelo Sommerfeld explicou com sucesso que os elétrons com o mesmo número quântico principal n diferem em seu estado de energia, porque eles podem ter diferentes números quânticos l e m L .
-Introduziu a constante α para desenvolver a estrutura fina do espectro atômico e explicar o efeito Zeeman.
Efeitos relativísticos incluídos, já que os elétrons podem se mover com velocidades bem próximas da velocidade da luz.
Desvantagens
-Seu modelo era aplicável apenas a átomos com um elétron e, de várias maneiras, a átomos de metais alcalinos como Li 2+ , mas não é útil no átomo de hélio, que possui dois elétrons.
-Não explicou a distribuição eletrônica no átomo.
-O modelo permitiu calcular as energias dos estados permitidos e as frequências da radiação emitida ou absorvida nas transições entre estados, sem fornecer informações sobre os tempos dessas transições.
Agora, sabe-se que os elétrons não seguem caminhos com formas predeterminadas, como órbitas, mas ocupam orbitais , regiões do espaço que correspondem a soluções da equação de Schrodinger.
-O modelo combinou arbitrariamente aspectos clássicos com aspectos quânticos.
-Falha ao explicar o efeito anômalo de Zeeman, para isso é necessário o modelo Dirac, que mais tarde acrescentou outro número quântico.
Artigos de interesse
Modelo atômico de Schrödinger
Modelo atômico de Broglie.
Modelo atômico de Chadwick
Modelo atômico de Heisenberg.
Modelo atômico de Perrin.
Modelo atômico de Thomson
Modelo atômico de Dalton
Modelo atômico de Dirac Jordan.
Modelo atômico de Demócrito.
Modelo atômico de Bohr.
Referências
- Brainkart. Modelo de átomo de Sommerfeld e suas desvantagens. Recuperado de: brainkart.com.
- Como conhecemos o cosmos: luz e matéria. Átomo de Sommerfeld. Recuperado de: thestargarden.co.uk
- Parker, P. O átomo de Bohr-Sommerfeld. Recuperado de: physnet.org
- Canto Educacional. Modelo Sommerfeld. Recuperado de: rinconeducativo.com.
- Wikipedia. Modelo atômico de Sommerfeld Recuperado de: es.wikipedia, org.