O módulo de Young é uma propriedade mecânica importante que descreve a rigidez de um material, ou seja, a sua capacidade de resistir à deformação sob tensão. Neste contexto, o módulo de Young é uma medida da relação entre a tensão aplicada e a deformação resultante em um material. Neste artigo, vamos explorar como calcular o módulo de Young, suas aplicações práticas em engenharia e ciência dos materiais, exemplos de materiais com diferentes módulos de Young e exercícios para ajudar na compreensão e prática deste conceito fundamental.
Descubra a fórmula para calcular o módulo de Young de um material.
O módulo de Young é uma propriedade fundamental dos materiais que descreve sua rigidez e resistência à deformação. Para calcular o módulo de Young de um material, é necessário conhecer a tensão aplicada e a deformação resultante.
A fórmula para o cálculo do módulo de Young é dada por:
E = σ / ε
Onde:
E é o módulo de Young,
σ é a tensão aplicada ao material, e
ε é a deformação resultante.
Para aplicar a fórmula, basta dividir a tensão pela deformação para obter o módulo de Young. Este valor é expresso em unidades de pressão, como pascal (Pa) ou megapascal (MPa).
O módulo de Young é amplamente utilizado em engenharia para determinar a resistência de um material à deformação sob tensão. Quanto maior o módulo de Young, mais rígido e resistente é o material.
Um exemplo prático de aplicação do módulo de Young é na fabricação de estruturas de pontes e edifícios, onde é essencial garantir a segurança e estabilidade das construções sob carga.
Para fixar o conceito, vamos resolver um exercício simples de cálculo do módulo de Young:
Suponha que um material sofra uma deformação de 0,002 m quando submetido a uma tensão de 200 MPa. Qual é o módulo de Young do material?
Usando a fórmula E = σ / ε, temos:
E = 200 MPa / 0,002 m = 100.000 MPa
Portanto, o módulo de Young do material é de 100.000 MPa.
Qual a utilidade do módulo de elasticidade na engenharia e materiais?
O módulo de elasticidade, também conhecido como módulo de Young, é uma propriedade fundamental dos materiais que descreve a capacidade de um material de sofrer deformação elástica sob a ação de uma força externa. Este conceito é de extrema importância na engenharia e materiais, pois permite prever o comportamento mecânico de um material sob diferentes condições de carga.
Em termos simples, o módulo de elasticidade indica a rigidez de um material, ou seja, a resistência que ele oferece à deformação. Materiais com alto módulo de elasticidade são mais rígidos e menos propensos a deformações permanentes, enquanto materiais com baixo módulo de elasticidade são mais flexíveis e deformam-se facilmente.
Na prática, o módulo de elasticidade é utilizado para calcular a deformação de um material sob determinada carga, para projetar estruturas que suportem cargas específicas, para determinar a capacidade de um material de suportar tensões sem falhar, entre outras aplicações.
Por exemplo, ao projetar uma ponte, é necessário calcular o módulo de elasticidade do concreto utilizado nas colunas para garantir que a estrutura seja capaz de suportar o peso dos veículos que irão atravessá-la. Da mesma forma, na indústria aeroespacial, o módulo de elasticidade dos materiais utilizados na construção de aeronaves é fundamental para garantir a resistência e durabilidade das mesmas.
Unidade de medida do módulo de Young: o que é e como calcular.
O módulo de Young é uma grandeza física que mede a rigidez de um material, ou seja, a sua capacidade de resistir à deformação quando submetido a uma força externa. Essa propriedade é muito importante na engenharia, pois permite prever como um material irá se comportar quando submetido a diferentes tipos de carga.
A unidade de medida do módulo de Young é o Newton por metro quadrado (N/m²) ou o Pascal (Pa). Para calcular o módulo de Young de um material, basta dividir a tensão aplicada pelo material pela deformação resultante. A fórmula para o cálculo do módulo de Young é:
Módulo de Young = Tensão / Deformação
Por exemplo, se um material é submetido a uma tensão de 100 N/m² e a deformação resultante é de 0,01 m, o módulo de Young desse material será de 10000 N/m² ou 10000 Pa.
O módulo de Young é utilizado em uma variedade de aplicações, como no cálculo de estruturas de construção, na fabricação de materiais e na engenharia de materiais. Ele também é utilizado em testes de tração para determinar a resistência de um material.
Sua unidade de medida é o Newton por metro quadrado (N/m²) ou o Pascal (Pa).
A relação entre o módulo de elasticidade e a deformação crescente.
O módulo de elasticidade, também conhecido como módulo de Young, é uma propriedade importante dos materiais que descreve a sua capacidade de resistir à deformação. Quanto maior o módulo de elasticidade de um material, maior será a sua rigidez e resistência à deformação.
Quando um material é submetido a uma força externa, ele sofre uma deformação. A relação entre o módulo de elasticidade e a deformação crescente é direta e proporcional. Isso significa que, à medida que a deformação aumenta, a tensão aplicada também aumenta de acordo com o módulo de elasticidade do material.
Por exemplo, se um material tem um módulo de elasticidade alto, ele suportará uma maior deformação antes de atingir o limite de sua capacidade. Por outro lado, se o módulo de elasticidade for baixo, o material se deformará mais facilmente sob a mesma carga.
Portanto, a relação entre o módulo de elasticidade e a deformação crescente é fundamental para entender o comportamento dos materiais sob tensão. O cálculo e a aplicação do módulo de Young são essenciais para projetar estruturas que sejam capazes de suportar cargas e deformações específicas.
Módulo de Young: cálculo, aplicações, exemplos, exercícios
O módulo de Young ou módulo de elasticidade é a constante que relaciona a tracção ou de compressão, com o respectivo aumento ou diminuição em comprimento, possuindo o objeto sob essas forças.
As forças externas aplicadas aos objetos podem não apenas mudar seu estado de movimento, mas também são capazes de mudar de forma ou até mesmo quebrá-las ou fraturá-las.

O módulo de Young é usado para estudar as alterações produzidas em um material quando uma força de tração ou compressão é aplicada externamente. É muito útil em assuntos como engenharia ou arquitetura.
Qual é o modelo de Young?
Quanto um objeto pode ser deformado? Isso é algo que os engenheiros geralmente querem saber. A resposta dependerá das propriedades do material e de suas dimensões.
Por exemplo, duas barras de alumínio com diferentes dimensões podem ser comparadas. Cada um tem uma área de seção transversal e comprimento diferentes, e ambos são submetidos à mesma força de tração.
O comportamento esperado será o seguinte:
– Quanto mais espessa (seção transversal) da barra, menos esticada.
– Quanto maior o comprimento inicial, maior o alongamento final.
Isso faz sentido, porque, afinal, a experiência indica que não é o mesmo tentar deformar um elástico do que tentar fazê-lo com uma barra de aço.
Um parâmetro chamado módulo de elasticidade do material é uma indicação de sua resposta elástica. O módulo de elasticidade é nomeado em homenagem a Thomas Young (1773-1829), um cientista britânico versátil que fez grandes contribuições para a ciência em muitas áreas.
Como físico, Young não apenas estudou a natureza ondulatória da luz, revelada com o famoso experimento de dupla fenda, mas também foi médico, linguista e até contribuiu para decifrar parte dos hieróglifos egípcios da famosa pedra de Roseta.
Como é calculado?
Sendo médico, Young queria conhecer o papel da elasticidade das artérias no bom desempenho da circulação sanguínea. A partir de suas experiências, ele concluiu a seguinte relação empírica:
A tensão é proporcional à deformação, desde que o limite elástico do material não seja excedido.
É possível representar graficamente o comportamento de um material antes da aplicação de um esforço, conforme mostrado na figura a seguir.

Da origem ao ponto A
Na primeira seção, que vai da origem ao ponto A, o gráfico é uma linha reta. Existe a lei de Hooke válida:
F = kx
Onde F é a magnitude da força que retorna o material ao seu estado original, x é a deformação experimentada por ele e k é uma constante que depende do objeto sujeito à tensão.
As deformações consideradas aqui são pequenas e o comportamento é perfeitamente elástico.
De A a B
De A a B, o material também se comporta de maneira elástica, mas a relação entre tensão e deformação não é mais linear.
De B para C
Entre os pontos B e C, o material sofre deformação permanente, não podendo retornar ao seu estado original.
De C
Se o material continuar a esticar do ponto C, ele eventualmente sofrerá uma pausa.
Matematicamente, as observações de Young podem ser resumidas da seguinte forma:
Esforço ∝ Deformação
Onde a constante de proporcionalidade é precisamente o módulo de elasticidade do material:
Esforço = Módulo de elasticidade x Deformação
Existem muitas maneiras de deformar os materiais. Os três tipos mais comuns de esforço para enviar um objeto são:
– tensão ou alongamento.
Compressão.
– Corte ou cisalhamento.
Um esforço ao qual os materiais são comumente submetidos, por exemplo na construção civil ou em peças automotivas, é a tração.
Fórmulas
Quando um objeto de comprimento L é esticado ou esticado, ele está sendo sujeito a tração que causa uma variação em seu comprimento. Um esboço dessa situação é representado na Figura 3.
Isso requer que uma força de magnitude F por unidade de área seja aplicada em suas extremidades, para causar alongamento, de modo que seu novo comprimento se torne L + DL.
O esforço feito para deformar o objeto será precisamente essa força por unidade de área, enquanto a deformação unitária experimentada é ΔL / L.
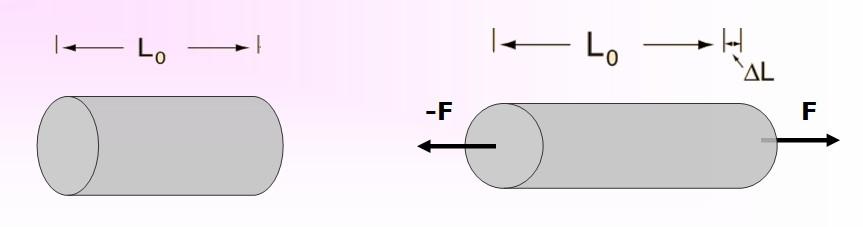
Denotando o módulo de Young como Y e como mencionado acima:

A resposta está no fato de que a deformação unitária indica a deformação relativa em relação ao comprimento original. Não é o mesmo que uma barra de 1 m que se estende ou encolhe 1 cm, de modo que uma estrutura de 100 metros de comprimento também deforma 1 cm.
Para o bom funcionamento de peças e estruturas, há uma tolerância em relação às deformações relativas permitidas.
Equação para calcular a deformação
Se a equação anterior for analisada da seguinte forma:

– Quanto maior a área da seção transversal, menor a deformação.
– Maior comprimento, maior deformação.
– Quanto maior o módulo de Young, menor a deformação.
As unidades de esforço correspondem a newton / metro quadrado (N / m 2 ). Eles também são as unidades de pressão, que no Sistema Internacional são nomeadas Pascal. A deformação unitária ΔL / L, por outro lado, é adimensional porque é a razão entre dois comprimentos.
As unidades do sistema em inglês são lb / in 2 e também são usadas com muita frequência. O fator de conversão para alternar entre eles é: 14,7 lb / in 2 = 1,01325 x 10 5 Pa
Isso leva ao módulo de Young também tendo unidades de pressão. Finalmente, a equação anterior pode ser expressa para limpar Y :

Na ciência dos materiais, a resposta elástica destes a vários esforços é importante para selecionar o mais apropriado em cada aplicação, seja fabricando a asa de uma aeronave ou um rolamento automotivo. As características do material a ser usado são decisivas na resposta esperada dele.
Para escolher o melhor material, é necessário conhecer os esforços aos quais uma determinada peça será submetida; e, consequentemente, selecione o material que possui as propriedades mais consistentes com o design.
Por exemplo, a asa de um avião deve ser forte, leve e capaz de flexionar. Os materiais utilizados na construção dos edifícios devem suportar movimentos sísmicos em grande medida, mas também devem ter alguma flexibilidade.
Os engenheiros que projetam as asas da aeronave e também os que escolhem os materiais de construção devem usar gráficos de tensão-deformação, como mostra a Figura 2.
É possível realizar as medições para determinar as propriedades elásticas mais relevantes de um material em laboratórios especializados. Assim, existem testes padronizados aos quais as amostras são submetidas, às quais vários esforços são aplicados, medindo as deformações resultantes.
Exemplos
Como mencionado anteriormente, Y não depende do tamanho ou da forma do objeto, mas das características do material.
Outra observação muito importante: para que a equação acima seja aplicável, o material deve ser isotrópico , ou seja, suas propriedades devem permanecer inalteradas por toda a sua totalidade.
Nem todos os materiais são isotrópicos: existem aqueles cuja resposta elástica depende de certos parâmetros direcionais.
A deformação analisada nos segmentos anteriores é apenas uma das muitas às quais um material pode ser submetido. Por exemplo, em termos de esforço de compressão, é o oposto do estresse por tensão.
As equações dadas se aplicam a ambos os casos, e quase sempre os valores de Y são os mesmos (materiais isotrópicos).
Uma exceção notável é o concreto ou cimento, que resiste melhor à compressão do que à tração. Portanto, deve ser reforçado quando for necessária resistência ao alongamento. O aço é o material indicado para isso, porque resiste a esticar ou puxar muito bem.
Como exemplos de estruturas sob estresse estão as colunas de edifícios e arcos, elementos clássicos de construção em muitas civilizações antigas e modernas.

Exercícios resolvidos
Exercício 1
Um fio de aço de 2,0 m de comprimento em um instrumento musical tem um raio de 0,03 mm. Quando o cabo está sob uma tensão de 90 N: quanto muda seu comprimento? Fato : O módulo de aço de Young é de 200 x 10 9 N / m 2
Solução
É necessário calcular a área de seção transversal A = πR 2 = π. (0,03 x 10 -3 m) 2 = 2,83 x 10 -9 m 2
O esforço é a tensão por unidade de área:

Como a corda está sob tensão, isso significa que ela se alonga.
O novo comprimento é L = L ou + DL, onde L o é o comprimento inicial:
L = 2,32 m
Exercício 2
Uma coluna de mármore, cuja área de seção transversal é de 2,0 m 2, suporta uma massa de 25.000 kg. Localizar:
a) O esforço na coluna.
b) Deformação unitária.
c) Quanto a coluna é encurtada se a sua altura for de 12 m?
Fato : O módulo de mármore de Young é de 50 x 10 9 N / m 2
Solução
a) O esforço na coluna é devido ao peso de 25000 kg:
P = mg = 25000 kg x 9,8 m / s 2 = 245.000 N
Portanto, o esforço é:


ΔL = 2,45 x 10 -6 x 12 m = 2,94 x 10 -5 m = 0,0294 mm.
Não se espera que a coluna de mármore encolha significativamente. Observe que, embora o módulo de Young seja menor em mármore do que em aço, e que a coluna também tenha uma força muito maior, seu comprimento dificilmente varia.
Por outro lado, na sequência do exemplo anterior, a variação é muito mais perceptível, embora o aço tenha um módulo de Young muito maior.
Sua grande área de seção transversal intervém na coluna e, portanto, é muito menos deformável.
Referências
- Bauer, W. 2011. Física para Engenharia e Ciência. Volume 1. Mac Graw Hill. 422-527.
- Giancoli, D. 2006. Física: Princípios com Aplicações. Sexta Edição Prentice Hall. 238-249.