O Número de Reynolds é um parâmetro utilizado na mecânica dos fluidos para determinar o regime de escoamento de um fluido em um determinado sistema. Ele é calculado a partir da relação entre as forças inerciais e as forças viscosas presentes no fluido, sendo uma ferramenta importante para prever se o escoamento será laminar ou turbulento.
Para calcular o Número de Reynolds, utiliza-se a seguinte fórmula: Re = (ρ * V * D) / μ, onde ρ é a densidade do fluido, V é a velocidade do fluido, D é o diâmetro característico do sistema e μ é a viscosidade dinâmica do fluido.
Exercícios práticos de cálculo do Número de Reynolds são importantes para a compreensão e aplicação desse conceito na prática. Eles podem envolver situações como o escoamento de líquidos em tubulações, aeroportos de aviões, entre outros exemplos do cotidiano em que o conhecimento do Número de Reynolds é essencial para o correto dimensionamento e operação dos sistemas.
Descubra a fórmula para encontrar o número de Reynolds em sistemas fluidos.
O Número de Reynolds é um conceito fundamental em mecânica dos fluidos, que ajuda a determinar o regime de escoamento de um fluido em um determinado sistema. Ele é calculado a partir de três variáveis principais: a densidade do fluido (ρ), a velocidade do fluido (v) e o diâmetro característico do sistema (D).
A fórmula para encontrar o Número de Reynolds é dada por Re = ρ * v * D / μ, onde μ é a viscosidade dinâmica do fluido. Este número adimensional é utilizado para determinar se o escoamento é laminar, transicional ou turbulento.
Para calcular o Número de Reynolds, é importante conhecer as propriedades do fluido e as características do sistema em questão. Em sistemas como tubos, dutos e canais, o Número de Reynolds é essencial para prever o comportamento do fluido e dimensionar os equipamentos necessários.
Para exemplificar, vamos resolver um exercício utilizando a fórmula do Número de Reynolds. Suponha que um fluido com densidade de 1000 kg/m³, velocidade de 2 m/s e diâmetro de 0.1 m esteja fluindo em um tubo. Calcule o Número de Reynolds sabendo que a viscosidade dinâmica do fluido é de 0.01 kg/m.s.
Substituindo os valores na fórmula, temos: Re = 1000 * 2 * 0.1 / 0.01 = 20000. Portanto, o Número de Reynolds para esse sistema é de 20000, indicando um escoamento turbulento.
Em resumo, o Número de Reynolds é uma ferramenta importante na análise de sistemas fluidos, permitindo a previsão do comportamento do escoamento. Com a fórmula correta e o conhecimento das variáveis envolvidas, é possível calcular o Número de Reynolds e interpretar seu significado no contexto da mecânica dos fluidos.
Qual a utilidade do experimento de Reynolds na física e engenharia?
O experimento de Reynolds é de extrema importância na física e engenharia, pois permite estudar e compreender o comportamento de fluidos em diferentes situações. O Número de Reynolds, introduzido por Osborne Reynolds em 1883, é uma grandeza adimensional que desempenha um papel fundamental nesse experimento.
O Número de Reynolds é calculado pela fórmula: Re = (ρ * v * L) / μ, onde ρ é a densidade do fluido, v é a velocidade do fluido, L é o comprimento característico e μ é a viscosidade dinâmica do fluido. Ele representa a relação entre as forças inerciais e viscosas em um escoamento, indicando se o fluxo é laminar ou turbulento.
Para calcular o Número de Reynolds, é necessário conhecer as propriedades do fluido e as condições de escoamento. Com base nesse valor, é possível prever o comportamento do fluido e dimensionar equipamentos, como tubulações e bombas, de forma mais eficiente.
Além disso, o experimento de Reynolds permite visualizar de forma prática e didática a transição entre o escoamento laminar e turbulento, demonstrando as diferenças de padrões de fluxo e perdas de energia associadas a cada regime.
Em resumo, o Número de Reynolds e o experimento de Reynolds são ferramentas essenciais para o estudo e análise de escoamentos de fluidos na física e engenharia, proporcionando insights valiosos para o projeto e otimização de sistemas e processos que envolvem o transporte de fluidos.
Determinando o número de Reynolds da água a 20°C em tubo de 4 mm.
O número de Reynolds é um importante parâmetro utilizado na mecânica dos fluidos para determinar o regime de escoamento de um fluido em um determinado meio. Ele é calculado pela relação entre as forças inerciais e viscosas que atuam em um fluido em movimento, e é fundamental para prever se o escoamento será laminar ou turbulento.
Para calcular o número de Reynolds, é necessário conhecer a densidade e viscosidade do fluido, a velocidade do escoamento e as dimensões do meio em que o fluido está se movendo. No caso da água a 20°C em um tubo de 4 mm de diâmetro, podemos utilizar a seguinte fórmula:
Re = (Densidade x Velocidade x Diâmetro) / Viscosidade
Onde Re é o número de Reynolds, a densidade da água a 20°C é de aproximadamente 998 kg/m³, a viscosidade cinemática é de 1,002 x 10^-6 m²/s, a velocidade do escoamento é conhecida e o diâmetro do tubo é de 4 mm, ou seja, 0,004 m.
Substituindo os valores na fórmula, podemos determinar o número de Reynolds da água a 20°C em um tubo de 4 mm. Este valor nos indicará se o escoamento é laminar ou turbulento, auxiliando no dimensionamento de equipamentos e na previsão de perdas de carga.
Cálculo de escoamento turbulento: métodos e fórmulas para determinar a velocidade e fluxo.
O cálculo de escoamento turbulento é essencial para determinar a velocidade e o fluxo de um fluido em um determinado sistema. A turbulência ocorre quando o fluido se move de forma caótica, resultando em vórtices e instabilidades no fluxo. Para calcular o escoamento turbulento, é necessário utilizar métodos e fórmulas específicas que levam em consideração as propriedades do fluido e as condições de contorno do sistema.
Uma das formas mais comuns de determinar o comportamento de um escoamento turbulento é através do Número de Reynolds, que é uma grandeza adimensional utilizada para caracterizar o regime de escoamento de um fluido. O Número de Reynolds é calculado pela relação entre as forças inerciais e viscosas presentes no fluido, e é dado pela fórmula:
Re = (ρ * V * L) / μ
Onde Re é o Número de Reynolds, ρ é a densidade do fluido, V é a velocidade do fluido, L é o comprimento característico do sistema e μ é a viscosidade dinâmica do fluido.
Para determinar se o escoamento é turbulento, laminar ou de transição, é necessário comparar o valor do Número de Reynolds com valores de referência específicos para cada regime. Geralmente, valores de Reynolds maiores que 4000 indicam escoamento turbulento, enquanto valores menores que 2000 indicam escoamento laminar.
Para exemplificar o cálculo do Número de Reynolds, podemos considerar um tubo de diâmetro 0,1 m por onde flui água a uma velocidade de 2 m/s. Considerando a viscosidade dinâmica da água como 1 * 10^-3 Ns/m^2, podemos calcular o Número de Reynolds:
Re = (1000 * 2 * 0,1) / (1 * 10^-3) = 200000
Portanto, nesse caso, o escoamento da água no tubo seria considerado turbulento, de acordo com o valor do Número de Reynolds calculado.
Número de Reynolds: para que serve, como é calculado, exercícios
O número de Reynolds ( R e ) é uma grandeza numérica adimensional que estabelece a relação entre as forças de inércia e forças de viscosidade de um fluido em movimento. As forças inerciais são determinadas pela segunda lei de Newton e são responsáveis pela aceleração máxima do fluido. Forças viscosas são as forças que se opõem ao movimento do fluido.
O número de Reynolds se aplica a qualquer tipo de fluxo de fluido, como o fluxo em dutos circulares ou não circulares, em canais abertos, e o fluxo ao redor de corpos submersos.
O valor do número de Reynolds depende da densidade, viscosidade, velocidade do fluido e as dimensões do caminho atual. O comportamento de um fluido, dependendo da quantidade de energia que se dissipa, devido ao atrito, dependerá do fluxo ser laminar, turbulento ou intermediário. Por esse motivo, é necessário encontrar uma maneira de determinar o tipo de fluxo.
Uma maneira de determinar isso é por métodos experimentais, mas eles exigem muita precisão nas medições. Outra maneira de determinar o tipo de fluxo é através da obtenção do número de Reynolds.
Em 1883, Osborne Reynolds descobriu que, se o valor desse número adimensional for conhecido, pode ser previsto o tipo de fluxo que caracteriza qualquer situação de condução de fluidos.
Para que serve o número de Reynolds?
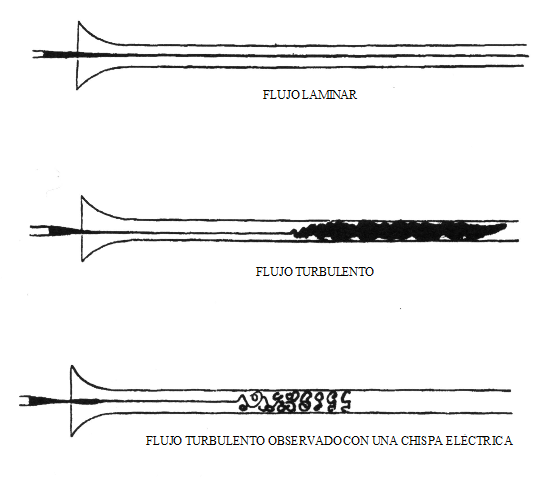
O número de Reynolds serve para determinar o comportamento de um fluido, isto é, para determinar se o fluxo de um fluido é laminar ou turbulento. O fluxo é laminar quando as forças viscosas, que são opostas ao movimento do fluido, são as que dominam e o fluido se move com uma velocidade suficientemente pequena e em uma trajetória retilínea.
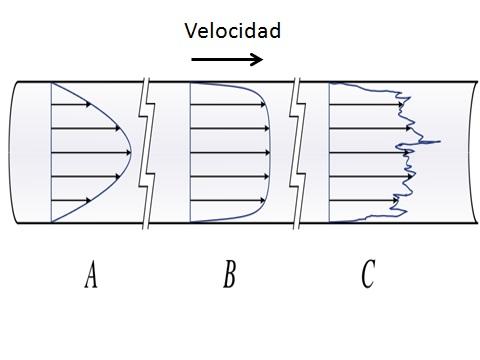
O fluido com fluxo laminar se comporta como se fossem camadas infinitas que deslizam umas sobre as outras, de maneira ordenada, sem se misturar. Nos dutos circulares, o fluxo laminar possui um perfil de velocidade parabólica, com valores máximos no centro do duto e valores mínimos nas camadas próximas à superfície do duto. O valor do número de Reynolds no fluxo laminar é R e <2000 .
O fluxo é turbulento quando as forças inerciais são dominantes e o fluido viaja com mudanças flutuantes na velocidade e trajetórias irregulares. O fluxo turbulento é muito instável e apresenta transferências de quantidade de movimento entre as partículas do fluido.
Quando o fluido circula em um duto circular, com fluxo turbulento, as camadas de fluido se cruzam entre si em redemoinhos e seu movimento tende a ser caótico. O valor do número de Reynolds para um fluxo turbulento em um duto circular é R e > 4000.
A transição entre fluxo laminar e fluxo turbulento ocorre para os valores numéricos de Reynolds entre 2000 e 4000.
Como é calculado?
A equação usada para calcular o número de Reynolds em um conduíte de seção transversal circular é:
R e = ρVD / η
ρ = densidade do fluido ( kg / m 3 )
V = Caudal ( m 3 / s )
D = Dimensão linear característica do percurso do fluido que, no caso do duto circular, representa o diâmetro.
η = viscosidade dinâmica do fluido ( Pa.s )
A relação entre viscosidade e densidade é definida como viscosidade cinemática v = η / ρ, e sua unidade é m 2 / s .
A equação do número de Reynolds em função da viscosidade cinemática é:
R e = VD / v
Em condutas e canais com secções transversais não circulares a dimensão característica é conhecido como diâmetro hidráulico D H e representa uma dimensão geral do curso do fluido.
A equação generalizada para calcular o número de Reynolds em dutos com seções transversais não circulares é:
R e = ρV´D H / η
V´ = vazão média = V / A
O diâmetro hidráulico D H estabelece a relação entre a área A da secção transversal da corrente de fluxo e o perímetro molhado P M .
D H = 4A / P M
O perímetro úmido P M é a soma dos comprimentos das paredes do duto, ou do canal, que estão em contato com o fluido.
Você também pode calcular o número de Reynolds de um fluido ao redor de um objeto. Por exemplo, uma esfera imerso num fluido que se move com velocidade V . A esfera experimenta uma força de arrasto F R definida pela equação de Stokes.
F R = 6πRVη
R = raio da esfera

O número de Reynolds de uma esfera com velocidade V submersa em um fluido é:
R e = ρV R / η
R e <1 quando o fluxo é laminar e R e > 1 quando o fluxo é turbulento.
Exercícios resolvidos
Abaixo estão três exercícios para aplicar o número de Reynolds: duto circular, duto retangular e esfera submersa em um fluido.
Número de Reynolds em um duto circular
Calcule o número de propileno glicol de Reynolds a 20 ° C em um ducto circular com um diâmetro de 0,5 cm . A magnitude da vazão é de 0,15 m 3 / s . Qual é o tipo de fluxo?
D = 0,5 centímetros = 5,10 -3 m (dimensão característica)
A densidade do fluido é ρ = 1.036 g / cm 3 = 1036 kg / m 3
A viscosidade do fluido é η = 0,042 Pa · s = 0,042 kg / ms
A vazão é V = 0,15 m 3 / s
A equação do número de Reynolds é usada em um duto circular.
R e = ρ VD / η
R e = ( 1036 kg / m 3 x0,15m 3 / sx 5,10 -3 m ) / (0,042 kg / ms) = 18,5
O fluxo é laminar porque o valor do número de Reynolds é baixo em relação à razão R e <2000
Número de Reynolds em um duto retangular
Determine o tipo de fluxo de etanol que flui com uma velocidade de 25 ml / min em um tubo retangular. As dimensões da seção retangular são de 0,5 cm e 0,8 cm.
Densidade ρ = 789 kg / m 3
Viscosidade dinâmica η = 1.074 mPa · s = 1.074,10 -3 kg / ms
Primeiro, a vazão média é determinada.
V´ = V / A
V = 25 ml / min = 4.16.10 -7 m 3 / s
A seção transversal é retangular cujos lados são 0,005m e 0,008m. A cruz – área da secção é A = 0,005 M x0,008m = 4.10 -5 m 2
V´ = (4.16.10 -7 m 3 / s) / ( 4.10 -5 m 2 ) = 1.04 × 10 -2 m / s
O perímetro úmido é a soma dos lados do retângulo.
P M = 0,013m
O diâmetro hidráulico é D H = 4A / P M
D H = 4 × 4,10 -5 m 2 / 0,013 m
D H = 1,23-10 -2 m
O número de Reynolds é obtido a partir da equação R e = ρV´ D H / η
R e = (789 kg / m 3 x1,04 × 10 -2 m / sx 1,23.10 -2 m) / 1.074,10 -3 kg / ms
R e = 93974
O fluxo é turbulento porque o número de Reynolds é muito grande ( R e > 2000)
Reynolds o número de esferas submersas em um fluido
Uma partícula esférica, látex de poliestireno, cujo raio é R = 2000nm é lançada na vertical na água com uma velocidade de magnitude inicial V 0 = 10 m / s. Determinar o número de Reynolds da partícula submersa em água
Densidade da partícula ρ = 1,04 g / cm 3 = 1040 kg / m 3
R = 2000nm = 0,000002m
Densidade da água ρ ag = 1000 kg / m 3
Viscosidade η = 0,001 kg / (m · s)
O número de Reynolds é obtido pela equação R e = ρV R / η
R e = (1000 kg / m 3 x 10 m / s x 0,000002m) / 0,001 kg / (m · s)
R e = 20
O número de Reynolds é 20. O fluxo é turbulento.
Aplicações
O número de Reynolds desempenha um papel importante na mecânica dos fluidos e na transferência térmica, pois é um dos principais parâmetros que caracterizam um fluido. Aqui estão algumas de suas aplicações.
1-É usado para simular o movimento de organismos que se movem em superfícies líquidas, tais como: bactérias suspensas na água que nadam através do fluido e produzem agitação aleatória.
2-Possui aplicações práticas no fluxo de tubos e canais de circulação de líquidos, fluxos confinados, principalmente em meios porosos.
3-Nas suspensões de partículas sólidas imersas em fluido e emulsões.
4 – O número de Reynolds é aplicado em ensaios em túneis de vento para estudar as propriedades aerodinâmicas de várias superfícies, especialmente no caso de voos de avião.
5-É usado para modelar o movimento de insetos no ar.
6-O projeto de reatores químicos requer o uso do número de Reynolds para escolher o modelo de fluxo, levando em consideração as perdas de carga, consumo de energia e área de transmissão de calor.
7-Na previsão de transferência de calor de componentes eletrônicos (1).
8-No processo de regar os jardins e pomares em que você precisa conhecer o fluxo de água que sai dos canos. Para obter essas informações, é determinada a perda de carga hidráulica, a qual está relacionada ao atrito entre a água e as paredes dos tubos. A perda de carga é calculada assim que o número de Reynolds é obtido.

Aplicações em Biologia
Em Biologia, o estudo do movimento de organismos vivos através da água ou em fluidos com propriedades semelhantes à água exige a obtenção do número de Reynolds, que dependerá do tamanho dos organismos e da velocidade com que eles deslocar.
Bactérias e organismos unicelulares têm um número de Reynolds muito baixo ( R e << 1 ), consequentemente, o fluxo possui um perfil de velocidade laminar com predominância de forças viscosas.
Organismos com um tamanho próximo a formigas (até 1 cm) têm um número de Reynolds da ordem de 1, o que corresponde ao regime de transição em que as forças inerciais que atuam no organismo são igualmente importantes como as forças viscosas do fluido.
Em organismos maiores, como as pessoas, o número de Reynolds é muito grande ( R e >> 1 ).
Referências
- Aplicação de modelos de fluxo turbulento com baixo número de Reynolds na previsão de transferência de calor de componentes eletrônicos. Rodgers, P e Eveloy, V. NV: sn, 2004, IEEE, Vol. 1, p. 495-503.
- Mott, R L. Applied Fluid Mechanics. Berkeley, CA: Pearson Prentice Hall, 2006, Vol. I.
- Collieu, AM e Powney, D. J. As propriedades mecânicas e térmicas dos materiais. Nova York: Crane Russak, 1973.
- Kay, JM e Nedderman, R M. Uma Introdução à Mecânica dos Fluidos e Transferência de Calor. Nova York: Cambridge Universitty Press, 1974.
- Happel, J e Brenner, H. Mecânica dos fluidos e processos de transporte. Hingham, MA: Martinus Nijhoff Publishers, 1983.