Uma pirâmide hexagonal é um sólido geométrico formado por uma base hexagonal e faces triangulares que se encontram em um vértice comum. Essa pirâmide tem seis faces laterais, que são triângulos, e uma base com seis lados. Suas características incluem ter 12 arestas, sendo seis delas nas faces laterais e seis na base, e sete vértices, incluindo um vértice na base e seis vértices nas faces laterais.
Um exemplo de pirâmide hexagonal pode ser encontrada na forma da pirâmide de Gizé, no Egito, uma das Sete Maravilhas do Mundo Antigo. Outro exemplo é a pirâmide do Louvre, em Paris, que tem uma estrutura semelhante à pirâmide hexagonal. Essas estruturas são exemplos impressionantes da aplicação da geometria na arquitetura e na engenharia.
Características da pirâmide hexagonal: formas, arestas, vértices e faces em destaque.
As pirâmides hexagonais são sólidos geométricos que possuem uma base hexagonal e seis faces triangulares que convergem para um vértice comum. Essa forma única confere a pirâmide hexagonal características distintas que a diferenciam de outros tipos de pirâmides.
Uma das principais características da pirâmide hexagonal é a sua base, que é formada por um hexágono regular. Isso significa que todos os lados do hexágono são iguais em comprimento e todos os ângulos internos são iguais a 120 graus. Essa base confere estabilidade e simetria à pirâmide.
Além disso, a pirâmide hexagonal possui 12 arestas, sendo que seis delas são arestas da base hexagonal e as outras seis são as arestas que conectam os vértices da base ao vértice superior. Essas arestas proporcionam uma estrutura sólida e definem a forma da pirâmide.
Em relação aos vértices, a pirâmide hexagonal possui sete no total: um vértice na parte superior da pirâmide e seis vértices na base hexagonal. Os vértices são pontos de encontro das arestas e das faces da pirâmide, conferindo-lhe definição e precisão nas formas.
Por fim, as faces da pirâmide hexagonal são seis triângulos equiláteros que se encontram no vértice superior da pirâmide. Cada face é formada por três arestas e três vértices, criando uma superfície plana que delimita o espaço interno da pirâmide.
Em resumo, a pirâmide hexagonal se destaca por sua base hexagonal, suas arestas bem definidas, seus vértices precisos e suas faces triangulares. Essas características combinadas conferem à pirâmide hexagonal uma aparência única e uma estrutura sólida, tornando-a uma forma geométrica fascinante e versátil.
Principais características de uma pirâmide: entenda seus elementos e estrutura básica.
Uma pirâmide é um sólido geométrico formado por uma base, que pode ser de qualquer forma, e faces triangulares que se encontram em um ponto chamado vértice. As pirâmides são caracterizadas pela sua estrutura tridimensional e pela presença de uma base e vértice.
As principais características de uma pirâmide incluem:
Base: é a face da pirâmide que fica embaixo e pode ter qualquer forma geométrica, como quadrado, retângulo, triângulo, etc.
Vértice: é o ponto onde todas as arestas da pirâmide convergem.
Arestas: são as linhas que formam os lados das faces triangulares da pirâmide.
Altura: é a distância entre a base e o vértice da pirâmide.
Volume: é a medida do espaço ocupado pela pirâmide. O cálculo do volume de uma pirâmide depende da sua base e altura.
Exemplos de pirâmides: a Pirâmide de Quéops no Egito, as pirâmides de Gizé, as pirâmides de Teotihuacan no México e as pirâmides de Chichén Itzá na Guatemala são alguns dos exemplos mais conhecidos de pirâmides em todo o mundo.
Descubra o número de faces e vértices de uma pirâmide com base hexagonal.
Uma pirâmide hexagonal é um sólido geométrico com uma base em forma de hexágono e faces triangulares que convergem em um vértice. Para descobrir o número de faces e vértices de uma pirâmide com base hexagonal, é importante entender suas características.
Uma pirâmide hexagonal tem seis faces triangulares que se encontram em um vértice comum. Além disso, a base da pirâmide é um hexágono com seis lados. Isso significa que a pirâmide terá um total de sete faces: a base hexagonal e as seis faces triangulares.
Quanto aos vértices, uma pirâmide hexagonal terá um vértice na ponta da pirâmide, onde todas as faces se encontram. Além disso, cada uma das seis faces laterais terá um vértice onde se encontram com a base hexagonal. Portanto, uma pirâmide hexagonal terá um total de sete vértices.
Em resumo, uma pirâmide hexagonal possui sete faces e sete vértices. É importante lembrar que essas são as características básicas de uma pirâmide com base hexagonal, e esses números podem variar dependendo do tamanho e proporções do sólido.
Qual a posição na hierarquia da pirâmide social?
Na pirâmide hexagonal, a posição na hierarquia social varia de acordo com a distribuição dos elementos. Na base da pirâmide estão os elementos com menor importância, enquanto no topo estão os elementos mais importantes. Esta estrutura hierárquica é essencial para a organização da sociedade e define as relações de poder e influência entre os diferentes indivíduos e grupos.
Na pirâmide hexagonal, os elementos do meio possuem uma posição intermediária, com um nível de importância maior do que os da base, mas inferior aos do topo. Eles desempenham um papel crucial na manutenção da ordem social e no equilíbrio entre os diferentes estratos da sociedade.
Os exemplos de hierarquia na pirâmide hexagonal podem ser encontrados em diferentes contextos, como em organizações empresariais, instituições políticas e até mesmo em comunidades religiosas. Em cada um desses casos, a posição na hierarquia social determina o acesso a recursos, privilégios e oportunidades, influenciando diretamente a vida e as perspectivas dos indivíduos.
Portanto, compreender a posição na hierarquia da pirâmide social é fundamental para entender as dinâmicas de poder e prestígio em uma sociedade. Aqueles que ocupam os níveis mais altos da pirâmide têm mais poder e influência, enquanto aqueles na base enfrentam mais desafios e restrições em suas vidas.
Pirâmide hexagonal: definição, características e exemplos
Uma pirâmide hexagonal é um poliedro formado por um hexágono, que é a base, e seis triângulos que começam nos vértices do hexágono e coincidem em um ponto fora do plano que contém a base. Esse ponto de concorrência é conhecido como o ápice ou ápice da pirâmide.
Um poliedro é um corpo geométrico tridimensional fechado cujas faces são figuras planas. Um hexágono é uma figura plana fechada (polígono) formada por seis lados. Se todos os seis lados têm o mesmo comprimento e formam ângulos iguais, diz-se regular; caso contrário, é irregular.

Definição de
Uma pirâmide hexagonal contém sete faces, a base e os seis triângulos laterais, dos quais a base é a única que não toca o vértice.
Diz-se que a pirâmide é reta se todos os triângulos laterais são isósceles. Nesse caso, a altura da pirâmide é o segmento que vai do vértice ao centro do hexágono.
Em geral, a altura de uma pirâmide é a distância entre o vértice e o plano da base. Diz-se que a pirâmide é oblíqua se nem todos os triângulos laterais são isósceles.
Se o hexágono é regular e a pirâmide também é reta, diz-se que é uma pirâmide hexagonal regular. Da mesma forma, se o hexágono é irregular ou a pirâmide é oblíqua, diz-se que é uma pirâmide hexagonal irregular.
Caracteristicas
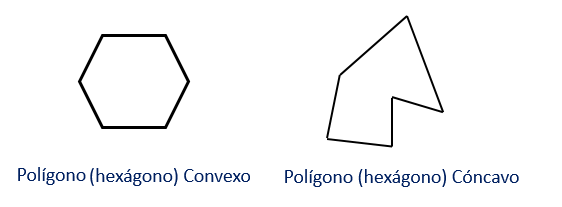
Côncavo ou convexo
Um polígono é convexo se a medida de todos os ângulos internos for menor que 180 graus. Geometricamente, isso equivale a dizer que, dados alguns pontos dentro do polígono, o segmento de linha que os une está contido no polígono. Caso contrário, diz-se que o polígono é côncavo.
Se o hexágono é convexo, diz-se que a pirâmide é uma pirâmide hexagonal convexa. Caso contrário, será dito que é uma pirâmide hexagonal côncava.
Bordas
As arestas de uma pirâmide são os lados dos seis triângulos que a compõem.
Apothem
O apótema da pirâmide é a distância entre o vértice e os lados da base da pirâmide. Essa definição só faz sentido quando a pirâmide é regular, porque, se for irregular, essa distância varia dependendo do triângulo considerado.
Em contraste, nas pirâmides regulares, o apótema corresponderá à altura de cada triângulo (já que cada um é isósceles) e será o mesmo em todos os triângulos.
O apótema da base é a distância entre um dos lados da base e o centro da mesma. Pela maneira como é definido, o apótema da base também faz sentido apenas nas pirâmides regulares.
Denotações
A altura de uma pirâmide hexagonal será indicada por h , o apótema da base (no caso regular) por APb e o apótema da pirâmide (também no caso regular) por AP .
Uma característica das pirâmides hexagonais regulares é que h , APB e AP formar um direito triângulo hipotenusa AP e pernas h e APB . Pelo teorema de Pitágoras, você tem que AP = √ (h ^ 2 + APb ^ 2).
A imagem acima representa uma pirâmide regular.
Como calcular a área? Fórmulas
Considere uma pirâmide hexagonal regular. Seja adaptado para cada lado do hexágono. Então A corresponde à medida da base de cada triângulo da pirâmide e, portanto, às arestas da base.
A área de um polígono é o produto do perímetro (a soma dos lados) pelo apótema da base, dividido entre dois. No caso de um hexágono, seria 3 * A * APb.
Pode-se observar que a área de uma pirâmide hexagonal regular é igual a seis vezes a área de cada triângulo da pirâmide mais a área da base. Como mencionado anteriormente, a altura de cada triângulo corresponde ao apótema da pirâmide, AP.
Portanto, a área de cada triângulo na pirâmide é dada por A * AP / 2. Assim, a área de uma pirâmide hexagonal regular é 3 * A * (APb + AP), onde A é uma aresta da base, APb é o apótema da base e AP o apótema da pirâmide.
Cálculo em pirâmides hexagonais irregulares
No caso de uma pirâmide hexagonal irregular, não existe uma fórmula direta para calcular a área, como no caso anterior. Isso ocorre porque cada triângulo da pirâmide terá uma área diferente.
Nesse caso, a área de cada triângulo deve ser calculada separadamente e a área da base. Então, a área da pirâmide será a soma de todas as áreas calculadas anteriormente.
Como calcular o volume? Fórmulas
O volume de uma pirâmide hexagonal regular é o produto da altura da pirâmide pela área da base entre três. Assim, o volume de uma pirâmide hexagonal regular é dado por A * APb * h, onde A é uma aresta da base, APb é o apótema da base e h é a altura da pirâmide.
Cálculo em pirâmides hexagonais irregulares
Da mesma forma que a área, no caso de uma pirâmide hexagonal irregular, não existe uma fórmula direta para calcular o volume, já que as bordas da base não têm a mesma medida porque é um polígono irregular.
Nesse caso, a área base deve ser calculada separadamente e o volume será (h * área base) / 3.
Exemplo
Calcule a área e o volume de uma pirâmide hexagonal regular com uma altura de 3 cm, cuja base é um hexágono regular de 2 cm de cada lado e o apótema da base é de 4 cm.
Solução
Primeiro, o apótema da pirâmide (AP) deve ser calculado, que é o único dado ausente. Observando a imagem acima, você pode ver que a altura da pirâmide (3 cm) e o apótema da base (4 cm) formam um triângulo retângulo; Portanto, o teorema de Pitágoras é usado para calcular o apótema da pirâmide:
Matemática5 pontos
Assim, usando a fórmula escrita acima, segue-se que a área é igual a 3 * 2 * (4 + 5) = 54cm ^ 2.
Por outro lado, usando a fórmula do volume, obtém-se que o volume da pirâmide especificada é 2 * 4 * 3 = 24cm ^ 3.
Referências
- Billstein, R., Libeskind, S., & Lott, JW (2013).Matemática: uma abordagem de resolução de problemas para professores do ensino fundamental. Editores López Mateos.
- Fregoso, RS, & Carrera, SA (2005).Matemática 3. Progreso Editorial.
- Gallardo, G. e Pilar, PM (2005).Matemática 6. Progreso Editorial.
- Gutiérrez, CT, & Cisneros, MP (2005).Curso de Matemática 3º. Editorial Progreso.
- Kinsey, L. & Moore, TE (2006).Simetria, forma e espaço: uma introdução à matemática através da geometria (ilustrado, reimpresso ed.). Springer Science & Business Media.
- Mitchell, C. (1999).Projetos deslumbrantes da linha matemática (ed. Ilustrado). Scholastic Inc.
- R., MP (2005).Eu desenho em sexto. Editorial Progreso.