“Quantos centésimos cabem em um décimo?” é uma pergunta comum quando se trata de frações decimais. Neste contexto, um décimo é equivalente a 10 centésimos, pois a palavra “décimo” indica que algo foi dividido em 10 partes iguais. Portanto, a resposta para essa pergunta é que cabem 10 centésimos em um décimo. Este conceito é fundamental para entender a relação entre diferentes frações decimais e sua representação numérica.
Qual a conversão de décimos para centésimos?
Para converter décimos em centésimos, basta multiplicar o número de décimos por 10. Isso ocorre porque cada décimo representa uma dezena de centésimos. Por exemplo, se tivermos 2 décimos, podemos convertê-los em centésimos multiplicando por 10, o que resulta em 20 centésimos.
Quantos centésimos cabem em um décimo?
Um décimo equivale a 10 centésimos. Isso significa que em um décimo há 10 partes iguais, cada uma delas correspondendo a um centésimo. Portanto, quando falamos em quantos centésimos cabem em um décimo, a resposta é 10 centésimos.
Qual o valor de 1 décimo em fração decimal?
Para determinar o valor de 1 décimo em fração decimal, basta dividir o número 1 pelo número 10. Dessa forma, temos que 1 décimo é equivalente a 0,1 em forma decimal.
Quantos centésimos cabem em um décimo?
Para descobrir quantos centésimos cabem em 1 décimo, basta lembrar que um décimo é equivalente a 10 centésimos. Portanto, em um décimo cabem exatamente 10 centésimos.
Quantas vezes o número 1 cabe no número 10?
Para entender quantas vezes o número 1 cabe no número 10, precisamos pensar em termos de frações. Um décimo é representado por 0,1, o que significa que um décimo é composto por 10 centésimos. Portanto, podemos dizer que um décimo equivale a 10 centésimos.
Agora, se quisermos descobrir quantos centésimos cabem em um décimo, basta dividir 1 por 0,1. Isso nos dá o resultado de 10. Ou seja, um décimo contém 10 centésimos.
Da mesma forma, quando pensamos em quantas vezes o número 1 cabe no número 10, podemos aplicar a mesma lógica. Dividindo 10 por 1, obtemos o resultado de 10. Portanto, o número 1 cabe 10 vezes no número 10.
Em resumo, um décimo contém 10 centésimos e o número 1 cabe 10 vezes no número 10.
Quantos centésimos correspondem a uma unidade inteira?
Quando falamos em centésimos, estamos nos referindo a uma divisão da unidade em cem partes iguais. Ou seja, um centésimo corresponde a 1/100 da unidade inteira. Portanto, cem centésimos correspondem a uma unidade inteira. Em outras palavras, um inteiro é igual a cem centésimos.
Quantos centésimos cabem em um décimo?
Um décimo, como o próprio nome sugere, representa uma divisão da unidade em dez partes iguais. Portanto, um décimo corresponde a dez centésimos. Para calcular quantos centésimos cabem em um décimo, basta multiplicar o número de décimos (10) pela quantidade de centésimos em cada décimo (10), o que resulta em cem centésimos. Em resumo, um décimo equivale a cem centésimos.
Quantos centésimos cabem em um décimo?
Antes de saber quantos centésimos cabem em um décimo, os conceitos de décimos e centésimos devem ser esclarecidos. O conceito a partir do qual essas palavras surgem é o de uma fração decimal.
O uso de frações decimais é mais cotidiano do que você pode imaginar. Eles podem ser aplicados desde os preços de um produto em uma loja até o peso de uma cesta de frutas no supermercado.
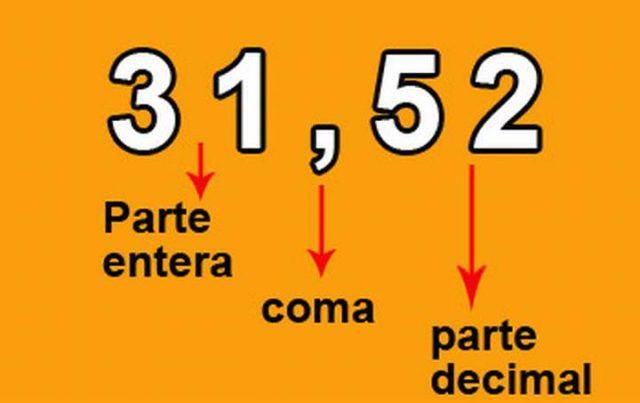
A vírgula na imagem é chamada de “ponto decimal”, mas na literatura inglesa e norte-americana é utilizado um “ponto” em vez da vírgula.
Fração decimal
Uma fração decimal é uma fração cujo denominador é 10, 100, 1.000, 10.000 ou qualquer outra potência de 10, daí a palavra decimal. Por exemplo 2 / 10.000, 53/10, 2.781 / 100, 321 / 1.000 são frações decimais.
Ao escrever uma fração decimal, o denominador é omitido e para indicar o valor do número em que um sinal (um ponto decimal) é colocado.
No número do numerador e à direita da vírgula, deve haver tantos números quanto zeros com o denominador correspondente.
Exemplos
– 2 / 10.000 seria escrito como 0,0002.
– 53/10 seria escrito como 5.3.
– 2.781 / 100 é escrito como 27,81.
– 321 / 1.000 é escrito como 0,321.
Por outro lado, a fração que representa o número da imagem anterior é 3.152 / 100, pois o número tem dois dígitos à direita do ponto decimal.
O número que está à esquerda da vírgula é chamado “número inteiro”, enquanto o número que está à direita é chamado de “parte decimal”.
Décimos, centésimos e milésimos
Assim como a parte inteira de um número é composta de unidades, dezenas e centenas nomeadas da direita para a esquerda, a parte decimal também é composta da esquerda para a direita em décimos, centésimos e milésimos.
Os décimos correspondem ao primeiro dígito à direita do ponto decimal e o denominador de sua fração decimal é 10. Por exemplo, 3 décimos (0,3) são iguais a 3/10.
Por outro lado, 46/10 é equivalente a 46 décimos e sua escrita decimal é 4.6, que também pode ser lida como 4 unidades com 6 décimos.
Da mesma forma, com os centésimos (segundo dígito à direita da vírgula decimal) e os milésimos (terceiro dígito à direita da vírgula decimal), cujos denominadores na fração decimal são 100 e 1.000, respectivamente.
Quantos centésimos cabem em um décimo?
Com o que está escrito acima, sabe-se que um décimo é igual a 1/10 e que um centésimo é 1/100. Em notação decimal, teremos que um décimo é 0,1 e um centésimo é 0,01.
A chave para responder a essa pergunta é saber quantas vezes você precisa adicionar um centésimo de si mesmo, para que o resultado seja apenas um décimo.
Se realizarmos os cálculos, veremos que temos que somar 1 centésimo 10 vezes consigo mesmo para obter um décimo.
Portanto, em um décimo ajuste 10 centavos.
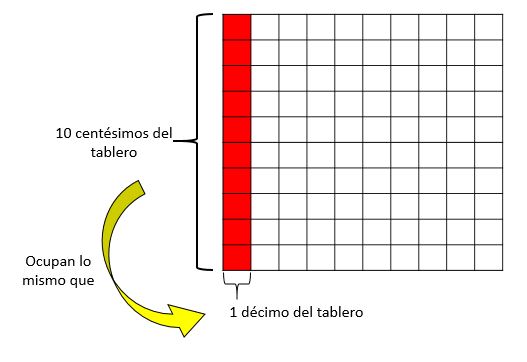
Outro processo que podemos usar para saber quantos centésimos cabem em um décimo é o seguinte: um quadro com 100 quadrados é ocupado; portanto, 1 quadrado do quadro representa um centésimo, enquanto qualquer coluna (ou linha) de 10 quadrados representa 1 décimo do quadro.
Portanto, para preencher uma linha (1 décimo), você precisa de 10 caixas (10 centésimos).
Referências
- Bourdon, PL (1860). Elementos aritméticos. Madri: Livraria de Don Ángel Calleja.
- Instituto Superior de Formação de Professores (Espanha); Jesus López Ruiz. (2004). Números, formas e volumes no ambiente da criança. Ministério da Educação.
- Mandri, F. (1837). Exercícios teóricos da aritmética. Campamar e Filhos.
- Martínez, JC (2014). Competição Matemática N2. Ideaspropias Editorial SL
- Mateos, ML (2013). O Royal Straight. Editores López Mateos.
- Palmer, CI, & Bibb, SF (1979). Matemática Prática: Aritmética, Álgebra, Geometria, Trigonometria e Regra de Cálculo (Reimpressão ed.). Reverte