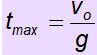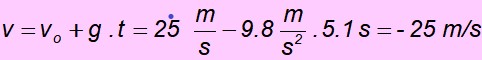Queda livre: conceito, equações, exercícios resolvidos

A queda livre é um fenômeno físico que ocorre quando um objeto é lançado de uma certa altura em direção à superfície da Terra, sem sofrer nenhuma influência externa, exceto a gravidade. Durante a queda livre, o objeto se move apenas na vertical, sem nenhuma aceleração horizontal.

Neste contexto, as equações da queda livre são fundamentais para calcular a velocidade, a altura e o tempo de queda de um objeto. Além disso, a resolução de exercícios práticos ajuda a compreender melhor os conceitos envolvidos e a aplicar as equações de forma eficiente.

Neste artigo, abordaremos o conceito de queda livre, apresentaremos as principais equações utilizadas para resolver problemas relacionados a esse fenômeno e resolveremos alguns exercícios práticos para exemplificar a aplicação dessas equações.

Equações empregadas na queda livre: quais são e como são aplicadas?

A queda livre é um fenômeno físico no qual um objeto é deixado cair de uma certa altura e só é influenciado pela força da gravidade. Para descrever matematicamente esse processo, utilizamos equações específicas que nos permitem calcular a posição, velocidade e tempo de queda de um objeto.

As equações mais comuns empregadas na queda livre são a equação da posição, a equação da velocidade e a equação do tempo. A equação da posição nos permite determinar a altura do objeto em relação ao ponto de partida, a equação da velocidade nos fornece a velocidade do objeto em queda e a equação do tempo nos diz quanto tempo o objeto leva para cair.

Para aplicar essas equações, é necessário conhecer a altura inicial do objeto, a aceleração da gravidade (que é aproximadamente 9,8 m/s²) e o tempo de queda. Com essas informações, podemos substituir os valores na equação correspondente e resolver para a incógnita desejada.

Por exemplo, se quisermos calcular a velocidade de um objeto em queda livre após 3 segundos, podemos utilizar a equação da velocidade, que é v = gt, onde v é a velocidade, g é a aceleração da gravidade e t é o tempo. Substituindo os valores conhecidos, temos v = 9,8 m/s² * 3 s = 29,4 m/s.

Portanto, as equações empregadas na queda livre são ferramentas essenciais para a compreensão e resolução de problemas relacionados a esse fenômeno físico. Com o conhecimento adequado dessas equações e sua aplicação correta, podemos fazer previsões precisas sobre o movimento de um objeto em queda livre.

Fórmula para calcular queda livre: qual é e como utilizá-la corretamente.

Queda livre é o movimento de um objeto que cai em direção à Terra sob a influência exclusiva da gravidade. Para calcular a queda livre de um objeto, podemos utilizar a fórmula matemática adequada.

A fórmula para calcular a queda livre é:

d = (1/2) * g * t^2

Onde:

d = distância percorrida durante a queda

g = aceleração da gravidade (aproximadamente 9,8 m/s^2 na superfície da Terra)

t = tempo de queda

Para utilizar corretamente essa fórmula, basta substituir os valores conhecidos de g e t e realizar os cálculos necessários. Assim, você poderá determinar a distância que um objeto caiu em queda livre em um determinado tempo.

É importante lembrar que a fórmula da queda livre é válida apenas em condições ideais, sem levar em consideração fatores como resistência do ar ou forças externas que possam influenciar o movimento do objeto em queda.

Para fixar o conceito e praticar o cálculo da queda livre, é possível resolver alguns exercícios que envolvam a aplicação da fórmula apresentada. Com a prática constante, você poderá aprimorar suas habilidades em física e compreender melhor os princípios por trás da queda livre.

Tempo de queda de fruta a 20m de altura sem resistência do ar.

A queda livre é um conceito da física que descreve o movimento de um objeto sob a influência exclusiva da força da gravidade. Quando um objeto é solto de uma certa altura, ele cai em direção ao solo devido à ação da gravidade, sem qualquer resistência do ar. Nesse caso, é possível determinar o tempo que o objeto leva para atingir o solo.

Para calcular o tempo de queda de uma fruta a 20m de altura sem resistência do ar, podemos utilizar a equação da queda livre: d = (1/2)gt^2, onde d é a altura inicial do objeto (20m), g é a aceleração da gravidade (aproximadamente 9,8 m/s²) e t é o tempo de queda que queremos determinar.

Substituindo os valores conhecidos na equação, temos: 20 = (1/2) * 9,8 * t^2. Simplificando a equação, obtemos: 20 = 4,9 * t^2. Dividindo ambos os lados por 4,9, encontramos que t^2 = 20/4,9. Portanto, o tempo de queda da fruta é aproximadamente t = √(20/4,9) ≈ 2,02 segundos.

Assim, podemos concluir que uma fruta solta de uma altura de 20m levará cerca de 2,02 segundos para atingir o solo em queda livre, sem considerar a resistência do ar.

Distância de queda em queda livre após 1 e 4 segundos de lançamento.

Queda livre é o movimento de um objeto em queda sob a influência exclusiva da gravidade, sem resistência do ar. Nesse tipo de movimento, a aceleração é constante e igual à aceleração da gravidade, aproximadamente 9,8 m/s². As equações que regem a queda livre são fundamentais para calcular a distância percorrida por um objeto em queda em determinado tempo.

Após 1 segundo de lançamento, a distância percorrida por um objeto em queda livre pode ser calculada pela equação d = (1/2)gt², onde d representa a distância percorrida, g é a aceleração da gravidade e t é o tempo decorrido. Substituindo os valores na equação, temos d = (1/2) * 9,8 * (1)² = 4,9 metros.

Já após 4 segundos de lançamento, a distância percorrida pode ser calculada pela mesma equação, considerando o tempo decorrido. Substituindo os valores, temos d = (1/2) * 9,8 * (4)² = 78,4 metros.

Portanto, após 1 segundo de lançamento, o objeto percorre uma distância de 4,9 metros, enquanto após 4 segundos, a distância percorrida é de 78,4 metros. Esses cálculos são essenciais para compreender o movimento de queda livre e sua relação com o tempo decorrido.

Queda livre: conceito, equações, exercícios resolvidos

A queda livre é o movimento vertical de um objeto sofre quando é deixado cair de uma certa perto da superfície da altura Terra. É um dos movimentos mais simples e imediatos conhecidos: em linha reta e com aceleração constante.

Todos os objetos que caem ou são jogados verticalmente para cima ou para baixo movem-se com a aceleração de 9,8 m / s ² fornecida pela gravidade da Terra, independentemente de sua massa.

Esse fato pode ser aceito hoje sem problemas. No entanto, a compreensão da verdadeira natureza da queda livre levou um tempo. Os gregos já o descreveram e interpretaram de maneira muito básica no século IV aC.

Conceito de queda livre de corpos

As idéias de Aristóteles

Aristóteles, o grande filósofo da antiguidade clássica, foi um dos primeiros a estudar a queda livre. Esse pensador observou que uma moeda estava caindo mais rápido que uma caneta. A caneta vibra quando cai, enquanto a moeda cai rapidamente no chão. Da mesma forma, uma folha de papel também leva tempo para chegar ao chão.

Portanto, Aristóteles não teve dúvidas em concluir que os objetos mais pesados ​​eram mais rápidos: um pedregulho de 20 quilos tinha que cair mais rápido que um pedregulho de 10 gramas. Os filósofos gregos não costumavam fazer experimentos, mas suas conclusões eram baseadas em observação e raciocínio lógico.

No entanto, essa idéia de Aristóteles, embora aparentemente lógica, estava realmente errada.

Vamos agora fazer o seguinte experimento: uma bola muito compacta é feita com a folha de papel e largada simultaneamente da mesma altura que a moeda. Observa-se que ambos os objetos atingem o solo ao mesmo tempo. O que poderia ter mudado?

Quando amassou o papel e compactou, sua forma mudou, mas não sua massa. O papel estendido tem mais superfície exposta ao ar do que quando compactado na forma de uma bola. É isso que faz a diferença. A resistência do ar afeta mais o objeto com maior superfície e reduz sua velocidade ao cair.

Quando a resistência do ar não é considerada, todos os objetos atingem o solo ao mesmo tempo, desde que caem da mesma altura. A Terra fornece uma aceleração constante de aproximadamente 9,8 m / s ² .

Galileu questionou Aristóteles

Centenas de anos se passaram depois que Aristóteles estabeleceu suas teorias sobre o movimento, até que alguém se atreveu a questionar suas idéias com experimentos reais.

As lendas dizem que Galileu Galilei (1564 – 1642) estudou a queda de diferentes corpos do topo da Torre de Pisa e reconheceu que todos caíram com a mesma aceleração, embora ele não tenha explicado o porquê. Isaac Newton cuidaria disso anos depois.

Não é certo que Galileu tenha realmente subido à Torre de Pisa para fazer suas experiências, mas é certo que ele se dedicou a fazê-las sistematicamente com a ajuda de um plano inclinado.

A idéia era rolar bolas ladeira abaixo e medir a distância percorrida até o fim. Posteriormente, a inclinação aumentou gradualmente, tornando o plano inclinado vertical. Isso é conhecido como “diluição da gravidade”.

Atualmente, é possível verificar se a caneta e a moeda caem simultaneamente quando são jogadas da mesma altura, se a resistência do ar não for considerada. Isso pode ser feito em uma câmara de vácuo.

Equações do movimento de queda livre

Uma vez convencido de que a aceleração é a mesma para todos os corpos liberados sob a ação da gravidade, é hora de estabelecer as equações necessárias para explicar esse movimento.

É importante enfatizar que a resistência do ar não é levada em consideração neste primeiro modelo de movimento. No entanto, os resultados deste modelo são muito precisos e próximos da realidade.

Em tudo o que se segue, o modelo de partículas será assumido, ou seja, as dimensões do objeto não serão levadas em consideração, assumindo que toda a massa esteja concentrada em um único ponto.

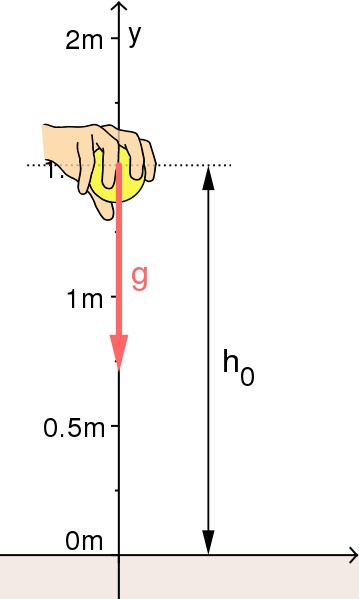
Para um movimento retilíneo uniformemente acelerado na direção vertical, ele é tomado como um eixo de referência para o eixo y. O sentido positivo é levado para cima e o negativo para baixo.

As magnitudes cinemáticas

Dessa forma, as equações de posição, velocidade e aceleração em função do tempo são:

Aceleração

a = g = -9,8 m / s ² (-32 pés / s ² )

Posição em função do tempo: y (t)

y = y _o + v _o . t + ½ gt ²

E onde _ou é a posição inicial de v móvel _ou a velocidade inicial. Lembre-se de que, na vertical, a velocidade inicial é necessariamente diferente de 0.

O que pode ser escrito como:

y – y _o = v _o . t + ½ gt ²

Δy = v _o . t + ½ gt ²

Com Δ e o deslocamento feito pela partícula em movimento. Nas unidades do Sistema Internacional, a posição e o deslocamento são dados em metros (m).

Velocidade em função do tempo: v (t)

v = v _ou + g. t

Velocidade dependendo do deslocamento

É possível deduzir uma equação que vincula deslocamento com velocidade, sem que o tempo intervenha nela. Para isso, o tempo da última equação é limpo:

Δy = v _o . t + ½ gt ²

A praça é desenvolvida com a ajuda do produto notável e os termos são reagrupados.

Essa equação é útil quando o tempo não está disponível, mas existem velocidades e deslocamentos, como será visto na seção de exemplos resolvidos.

Exemplos

O leitor atento deve ter notado a presença da velocidade inicial v _o . As equações acima são válidas para movimentos verticais sob a ação da gravidade, tanto quando o objeto cai de uma determinada altura, como se ele é jogado verticalmente para cima ou para baixo.

Quando o objeto é descartado, ele simplesmente se torna v _o = 0 e as equações são simplificadas da seguinte maneira.

Aceleração

a = g = -9,8 m / s ² (-32 pés / s ² )

Posição em função do tempo: y (t)

y = y _o + ½ gt ²

Velocidade em função do tempo: v (t)

v = g. t

Velocidade dependendo do deslocamento

v ² = 2g. Dy

Dy também será negativo, pois v ² deve ser uma quantidade positiva. Isso acontecerá se a origem ou o zero do sistema de coordenadas for obtido no ponto de lançamento ou no solo.

Se o leitor preferir, você pode tomar a direção descendente como positiva. A gravidade continuará a agir se for pensado em + 9,8 m / s ² . Mas você deve ser consistente com a convenção de sinal selecionada.

O lançamento vertical

Aqui, é claro, a velocidade inicial não pode ser zero. O objeto deve receber um impulso para subir. De acordo com a velocidade inicial fornecida, o objeto aumentará para uma altura maior ou menor.

Obviamente, haverá um momento em que o objeto pára momentaneamente. Em seguida, a altura máxima em relação ao ponto de lançamento será atingida. Além disso, a aceleração permanece baixa. Vamos ver o que acontece neste caso.

Cálculo da altura máxima atingida

Escolhendo-me = 0:

Como a gravidade sempre aponta para o chão na direção negativa, o sinal negativo é cancelado.

Cálculo do tempo máximo

Um procedimento semelhante é usado para encontrar o tempo que leva para o objeto atingir a altura máxima.

v = v _ou + g. t

Isso é feito v = 0

v _o = – g. t _max

Tempo de vôo é o tempo que o objeto dura no ar. Se o objeto retornar ao ponto inicial, o tempo de subida é igual ao tempo de descida. Portanto, o tempo de voo é 2. t máx.

É o dobro do tempo _{máximo que} o objeto dura no ar? Sim, desde que o objeto saia de um ponto e retorne a ele.

Se o lançamento for realizado a uma certa altura acima do solo e o objeto puder avançar em direção a ele, o tempo de voo não será mais o dobro do tempo máximo.

Exercícios resolvidos

O seguinte será considerado na resolução dos seguintes exercícios:

1-A altura de onde o objeto caiu é pequena em comparação com o raio da Terra.

2-A resistência do ar é insignificante.

3-O valor da aceleração da gravidade é 9,8 m / s ²

4-No caso de problemas com um único celular, preferencialmente é escolhido e _ou = 0 no ponto de partida. Isso geralmente facilita os cálculos.

5-Salvo indicação em contrário, a direção vertical para cima é considerada positiva.

6-Nos movimentos combinados para cima e para baixo, as equações aplicadas diretamente oferecem os resultados corretos, desde que seja mantida a consistência com os sinais: positivo para cima, negativo para baixo e gravidade -9,8 m / s ² ou -10 m / s ² se o arredondamento for preferido (por conveniência ao calcular).

Exercício 1

Uma bola é lançada verticalmente para cima com uma velocidade de 25,0 m / s. Responda às seguintes perguntas:

a) Quão alto ele aumenta?

b) Quanto tempo leva para chegar ao seu ponto mais alto?

c) Quanto tempo a bola leva para tocar a superfície da terra depois de atingir seu ponto mais alto?

d) Qual é a sua velocidade quando você retorna ao nível em que começou?

Solução

c) No caso de um lançamento nivelado: t _voo = 2. t _max = 2 x6 s = 5,1 s

d) Quando você retorna ao ponto inicial, a velocidade tem a mesma magnitude que a velocidade inicial, mas na direção oposta, portanto deve ser de – 25 m / s. É facilmente verificado substituindo valores na equação por velocidade:

Exercício 2

Uma pequena bolsa postal é liberada de um helicóptero que desce a uma velocidade constante de 1,50 m / s. Após 2,00 s, calcule:

a) Qual é a velocidade da bolsa?

b) Qual a distância da mala embaixo do helicóptero?

c) Quais são as suas respostas para as seções a) eb) se o helicóptero subir com uma velocidade constante de 1,50 m / s?

Solução

Seção para

Ao sair do helicóptero, a mala carrega sua velocidade inicial, portanto v _o = -1,50 m / s . Com o tempo indicado, a velocidade aumentou graças à aceleração da gravidade:

v = v _ou + g. t = -1,50 – (9,8 x 2) m / s = – 21,1 m / s

Seção b

Vamos ver quanto a mala caiu em comparação com o ponto de partida naquele momento:

Saco: Dy = v _o . t + ½ gt ² = -1,50 x 2 + ½ (-9,8) x 2 ² m = -22,6 m

Foi selecionado e _ou = 0 no ponto de partida, conforme indicado no início da seção. O sinal negativo indica que a bolsa caiu 22,6 m abaixo do ponto de partida.

Enquanto o helicóptero desceu rapidamente de -1,50 m / s, assumimos com rapidez constante, portanto, no tempo indicado de 2 segundos, o helicóptero viajou:

Helicóptero: Δy = v _ou .t = -1,50 x 2 m = -3 m.

Portanto, após 2 segundos, mala e helicóptero são separados por uma distância de:

d = | -22,6 – (-3) | m = 19. 6 m.

A distância é sempre positiva. Para destacar esse fato, o valor absoluto é usado.

Seção c

Quando o helicóptero sobe, ele tem uma velocidade de + 1,5 m / s. Com essa velocidade, a mala sai e, depois de 2 s, ela já carrega:

v = v _ou + g. t = +1,50 – (9,8 x 2) m / s = – 18,1 m / s

A velocidade acaba sendo negativa, pois após 2 segundos a bolsa está descendo. Aumentou graças à gravidade, mas não tanto quanto na seção a.

Agora vamos descobrir quanto a mala caiu do ponto de partida durante os primeiros 2 segundos de viagem:

Saco: Δ y = v _o . t + ½ gt ² = +1,50 x 2 + ½ (-9,8) x 2 ² m = -16,6 m

Enquanto isso, o helicóptero subiu do ponto de partida e o fez com velocidade constante:

Helicóptero: Δ y = v _ou .t = +1,50 x 2 m = +3 m.

Após 2 segundos, mala e helicóptero são separados por uma distância de:

d = | -16,6 – (+3) | m = 19,6 m

A distância que os separa é a mesma nos dois casos. A mala viaja menos distância vertical no segundo caso, porque sua velocidade inicial foi direcionada para cima.

Referências

1. Kirkpatrick, L. 2007. Física: Um olhar sobre o mundo. 6 ^ta Abridged Edition. Cengage Learning 23-27.
2. Rex, A. 2011. Fundamentos de Física. Pearson 33 – 36
3. Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14 ^th . Ed. Volume1. 50-53.
4. Serway, R., Vulle, C. 2011. Fundamentos de Física. 9 ^na Ed. Cengage Learning. 43-55.
5. Wilson, J. 2011. Física 10. Pearson Education. 133-149.