Come convertire frazioni improprie in frazioni proprie (e numeri misti)

Início » Ciência » Matemática » Come convertire frazioni improprie in frazioni proprie (e numeri misti)

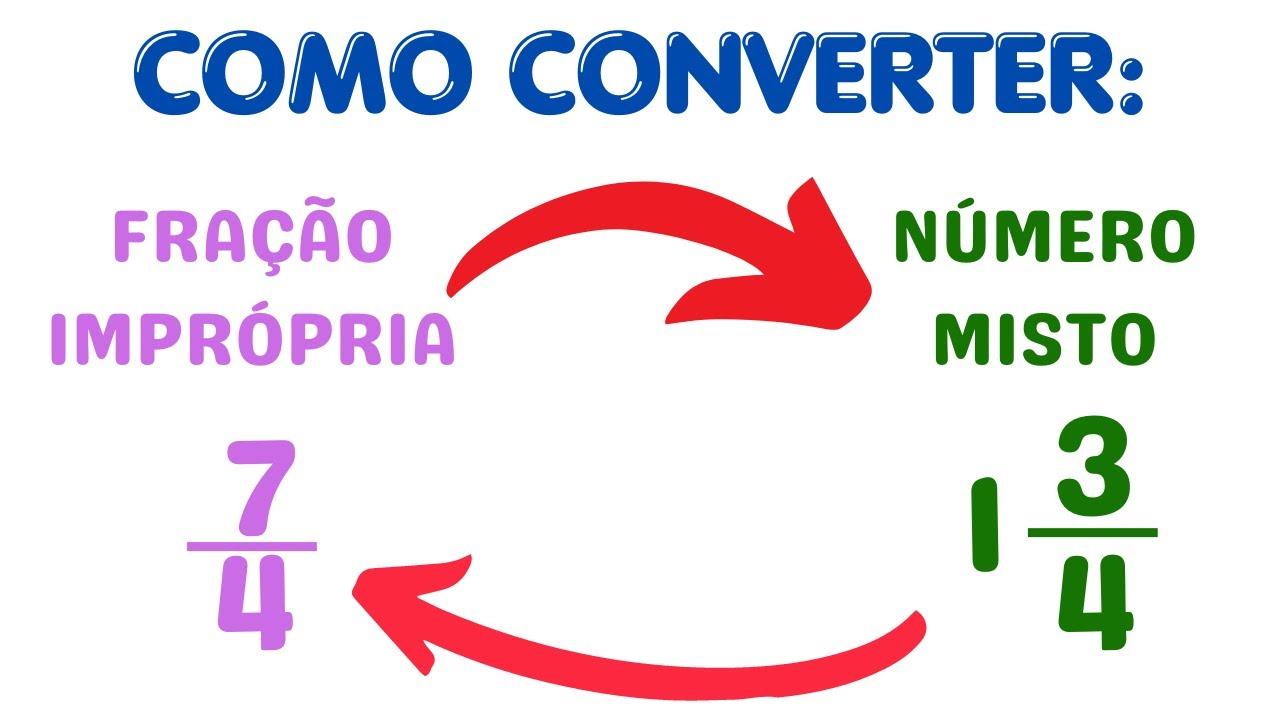
Quando si parla di frazioni a scuola o nella vita quotidiana, capita spesso di confondere i termini e i metodi. La distinzione tra frazioni proprie, improprie e apparenti è il punto di partenza per capire come scriverle e trasformarle senza errori, soprattutto quando vogliamo passare da una forma all’altra per leggere meglio la parte intera e la parte frazionaria.

Una domanda ricorrente è: si possono convertire le frazioni improprie in frazioni proprie? In realtà, una frazione impropria (con numeratore maggiore o uguale al denominatore) non può diventare una frazione propria equivalente con un unico numeratore e denominatore, perché il suo valore è maggiore o uguale a 1. Quello che facciamo è riscriverla come numero misto (parte intera + frazione propria) oppure come numero decimale.

Tipi di frazioni: proprie, apparenti e improprie

Per evitare malintesi, conviene fissare le definizioni. Una frazione è detta propria quando il numeratore è minore del denominatore, ad esempio 2/5 o 3/4: il suo valore è compreso tra 0 e 1.

Si chiama frazione apparente quella che, una volta semplificata o direttamente interpretata, rappresenta un numero intero. Per esempio 10/2 = 5, 12/4 = 3 e anche -25/5 = -5 sono casi in cui il risultato è un intero, quindi parliamo di frazioni apparenti.

Una frazione è impropria quando il numeratore supera (o è uguale a) il denominatore, senza rappresentare un intero esatto (se fosse esatto sarebbe apparente). Esempi classici sono 7/3, 13/5, 22/4 (che in prima battuta è impropria, poi si può semplificare).

Questa classificazione è utile perché, solo dalle frazioni improprie possiamo ricavare un numero misto con parte intera e parte frazionaria. Le frazioni proprie non hanno parte intera, e quelle apparenti coincidono con un numero intero.

Che cos’è un numero misto (o frazione mista)

Il numero misto (frazione mista) è una scrittura che combina un intero e una frazione propria. Serve per visualizzare chiaramente quanta parte intera c’è e quanta parte frazionaria rimane, ad esempio 2 3/5 si legge due e tre quinti.

Gli esempi aiutano: 3 2/5, 9 3/4, 1 1/2 sono tutti numeri misti. Questa forma è particolarmente comoda nella lettura di misure, ricette e problemi pratici, dove si vuole distinguere subito la parte intera da quella non intera.

Perché non si “converte” un’impropria in una propria (senza cambiare forma)

Un punto cruciale: una frazione impropria vale almeno 1; una frazione propria vale meno di 1. Perciò non esiste una frazione propria equivalente a una impropria: cambiare solo numeratore e denominatore mantenendo l’uguaglianza di valore non può produrre un numero minore di 1 da uno maggiore o uguale a 1.

Quello che facciamo di solito è riscrivere l’impropria come numero misto. In alternativa si può passare alla forma decimale (divisione tra numeratore e denominatore), ma quando interessa mantenere la logica delle frazioni, il numero misto è la soluzione standard.

Dal’impropria al numero misto: metodo passo per passo

La procedura è sempre la stessa: dividi il numeratore per il denominatore, individua quoziente e resto. Il quoziente è la parte intera, il resto diventa il nuovo numeratore della parte frazionaria, mentre il denominatore resta quello originale.

Primo esempio: 13/5. Facciamo 13 ÷ 5 = 2, con resto 3. La parte intera è 2 e la frazione residua è 3/5, quindi 13/5 = 2 3/5.

Secondo esempio: 17/3. Dividiamo 17 per 3: il quoziente è 5 e il resto è 2. Otteniamo 17/3 = 5 2/3, che rende immediata la lettura della quantità: cinque interi e due terzi.

Terzo esempio con semplificazione: 22/4. La divisione 22 ÷ 4 dà quoziente 5 e resto 2, quindi 22/4 = 5 2/4. La frazione 2/4 si può semplificare in 1/2, perciò la forma più pulita è 5 1/2.

Dal numero misto alla frazione impropria

La regola inversa è altrettanto semplice. Moltiplica la parte intera per il denominatore della frazione e somma il numeratore; il denominatore resta invariato. Così si torna a una singola frazione (impropria).

Esempio 1: 5 2/3. Calcoliamo (5 × 3) + 2 = 15 + 2 = 17. Il risultato è 17/3, cioè la stessa quantità espressa come frazione impropria.

Esempio 2: 9 3/4. Eseguiamo (9 × 4) + 3 = 36 + 3 = 39. Si ottiene 39/4, che è l’equivalente improprio del numero misto di partenza.

Esempi pratici e interpretazione

Molti contesti reali usano frazioni improprie e numeri misti. In cucina, dire 3/2 di tazza significa una tazza e mezza, cioè 1 1/2. Nell’edilizia o nel design, 7/4 metri si legge 1 3/4 m, un modo più intuitivo per capire le dimensioni.

In ambito finanziario, investire 5/2 di un capitale equivale a 2 capitali interi più mezzo. Nel linguaggio della statistica o della fisica, le frazioni improprie sono frequenti nelle medie, nei rapporti e nelle misure composte, dove la parte intera affiora naturalmente.

Operazioni con le frazioni improprie

Somma e differenza. Per addizione e sottrazione, serve portare le frazioni allo stesso denominatore (m.c.m.). Esempio: 5/3 + 7/4. Il m.c.m. tra 3 e 4 è 12, quindi 5/3 = 20/12 e 7/4 = 21/12: la somma è 41/12, ancora impropria.

Sottrazione d’esempio: 5/3 – 3/2. Con m.c.m. = 6, abbiamo 5/3 = 10/6 e 3/2 = 9/6. La differenza è 1/6, che invece è una frazione propria.

Prodotto. Per la moltiplicazione, si moltiplicano i numeratori tra loro e i denominatori tra loro: 5/3 × 2/3 = 10/9. Risultato: una frazione impropria che possiamo anche riscrivere come 1 1/9 se vogliamo evidenziare la parte intera.

Divisione. Per dividere frazioni, si moltiplica la prima per l’inverso della seconda: 5/3 ÷ 2/3 = (5/3) × (3/2) = 15/6. Semplificando 15/6 otteniamo 5/2, cioè 2 1/2 come numero misto.

Vantaggi della forma “mista”

Leggere un’impropria come numero misto spesso migliora la comprensione. La parte intera spicca subito e la frazione residua dice quanto manca all’intero successivo. Questo è pratico negli esercizi, nelle misure e nella comunicazione dei risultati.

Inoltre, quando si devono confrontare quantità, due numeri misti permettono paragoni rapidi osservando prima le parti intere e poi, se necessario, le frazioni rimanenti, senza passare per decimali infiniti o periodici.

Errori comuni e consigli utili

Errore n. 1: confondere frazione apparente e impropria. Se 12/4 = 3, non c’è parte frazionaria, quindi non è una frazione “mista” ma un intero. Errore n. 2: dimenticare di semplificare la frazione residua del numero misto (ad esempio 2/4 va ridotto a 1/2).

Errore n. 3: sbagliare quoziente e resto nella divisione. Controlla sempre: numeratore = denominatore × quoziente + resto, con il resto minore del denominatore. Se il resto è zero, hai una frazione apparente.

Consiglio: nelle somme e sottrazioni tra frazioni, usa il minimo comune multiplo (m.c.m.) per evitare denominatori enormi. Nelle moltiplicazioni e divisioni, semplifica prima incrociando fattori comuni per ridurre i numeri e gli errori di calcolo.

Piccolo glossario essenziale

Frazioni improprie: frazioni con numeratore maggiore o uguale al denominatore (valore ≥ 1, salvo essere apparenti se equivalgono a un intero).

Frazioni proprie: frazioni con numeratore minore del denominatore (valore tra 0 e 1).

Frazioni apparenti: scritture frazionarie che rappresentano un numero intero (es. 12/4 = 3).

Numeratore: il numero sopra la linea di frazione; Denominatore: il numero sotto la linea di frazione.

Numero misto: forma con parte intera più frazione propria (es. 2 3/5), utile per una lettura più intuitiva.

m.c.m. (minimo comune multiplo): il più piccolo multiplo condiviso da due o più numeri, usato per armonizzare i denominatori.

Conversione: passaggio tra impropria e numero misto (e viceversa) tramite divisione o combinazione intero×denominatore + numeratore.

Proporzioni e misure: contesti in cui le frazioni descrivono rapporti e quantità fisiche; compaiono spesso in ricette, costruzioni e dati sperimentali.

Equazioni algebriche: espressioni che possono includere frazioni improprie e richiedere semplificazioni per la risoluzione.

Cenni storici: il trattamento delle frazioni si è evoluto in molte civiltà; matematici come Al-Khwarizmi e Fibonacci hanno contribuito a diffonderne l’uso e la notazione.

Applicazioni: matematica, scienza, ingegneria e oltre

Nella geometria di aree e volumi è comune incontrare misure frazionarie: le frazioni improprie aiutano a sommare o moltiplicare porzioni oltre l’unità, che poi si possono rileggere come numeri misti per interpretare i risultati.

Nelle scienze applicate e in ingegneria, ratio e coefficienti possono superare l’unità; la forma impropria mantiene calcoli compatti, mentre la forma mista chiarisce il significato fisico della grandezza.

Anche in statistica capita di ottenere frazioni improprie durante medie o rapporti tra frequenze; passare alla forma mista facilita la comunicazione dei risultati a un pubblico non tecnico.

Ultimo, ma non meno importante, c’è la didattica: giochi, software e app interattive rendono più visiva la transizione tra impropria e mista, consolidando l’intuizione sulla parte intera e su ciò che resta.

Esempi guidati: dall’impropria alla mista

Esempio A: 27/5. Dividiamo 27 per 5: quoziente 5, resto 2. Scriviamo 27/5 = 5 2/5. Qui non c’è nulla da semplificare nella parte frazionaria, quindi la forma è già ottimale.

Esempio B: 41/12. 41 ÷ 12 = 3 con resto 5 (perché 3×12 = 36 e 41 – 36 = 5). Otteniamo 3 5/12, una lettura molto più immediata della quantità.

Esempio C: 15/6. La divisione con resto ci darebbe 2 3/6, ma 15/6 si semplifica prima a 5/2. Riscrivere 5/2 come 2 1/2 è ancora più chiaro, ed evita una frazione non ridotta come 3/6.

Esempi guidati: dalla mista all’impropria

Esempio D: 3 9/5. Calcolo: (3 × 5) + 9 = 15 + 9 = 24. La frazione è 24/5. Se preferiamo, possiamo tornare dopo a 4 4/5, ma in forma impropria è 24/5.

Esempio E: 1 1/2. Moltiplico 1 × 2 = 2, poi sommo 1: totale 3. Risultato 3/2, che sappiamo essere 1 1/2 in forma mista.

Esercizi svolti

Q1. Scrivi come numero misto la frazione 27/5.

Soluzione: 27 ÷ 5 = 5 con resto 2, quindi 27/5 = 5 2/5. La parte intera è 5 e la parte frazionaria è 2/5.

Q2. Trasforma il numero misto 9 3/4 in frazione impropria.

Soluzione: (9 × 4) + 3 = 36 + 3 = 39; si ottiene 39/4, già in forma semplificata.

Q3. Somma 5/3 e 7/4 e lascia il risultato come frazione impropria.

Soluzione: m.c.m.(3,4) = 12; 5/3 = 20/12 e 7/4 = 21/12, quindi 20/12 + 21/12 = 41/12. Possiamo anche dire 3 5/12 se vogliamo la forma mista.

Q4. Dividi 5/3 per 2/3 e semplifica.

Soluzione: 5/3 ÷ 2/3 = (5/3) × (3/2) = 15/6, che si semplifica in 5/2. Come numero misto vale 2 1/2.

Didattica e strumenti per imparare meglio

Gli insegnanti oggi ricorrono a schede, manipolativi e app per mostrare visivamente la scomposizione tra parte intera e parte frazionaria. Colorare “porzioni” di figure, usare blocchi o cerchi frazionati rende tangibile cosa significa passare da 13/5 a 2 3/5, per esempio.

Anche l’uso di software di algebra o calcolatrici con funzioni frazionarie è utile: consentono di verificare rapidamente quozienti e resti, e di sperimentare con la semplificazione, senza perdere la comprensione del procedimento.

Uno sguardo storico

Le frazioni sono antiche quanto la necessità di misurare e dividere. Nell’Egitto faraonico si usavano forme particolari; nel mondo arabo e poi in Europa medievale la notazione si è consolidata, fino a diventare quella che usiamo oggi.

Figure come Al-Khwarizmi e Fibonacci hanno avuto un ruolo fondamentale nella diffusione e nella didattica dei numeri razionali. Le loro opere hanno facilitato il passaggio da usi pratici a sistemi di calcolo più generali, aprendo la strada alla matematica moderna.

Comprendere come funzionano le frazioni improprie e come convertirle in numeri misti rende più semplice leggere, confrontare e calcolare quantità che superano l’unità. Definizioni chiare, procedimenti standard (divisione per ottenere quoziente e resto), esempi concreti e un po’ d’allenamento ti permettono di evitare gli errori tipici e di muoverti con disinvoltura tra somma, sottrazione, prodotto e quoziente di frazioni in ogni contesto: dallo studio alla vita reale.