Convertire frazioni in interi e decimali: guida chiara e completa

Início » Ciência » Matemática » Convertire frazioni in interi e decimali: guida chiara e completa

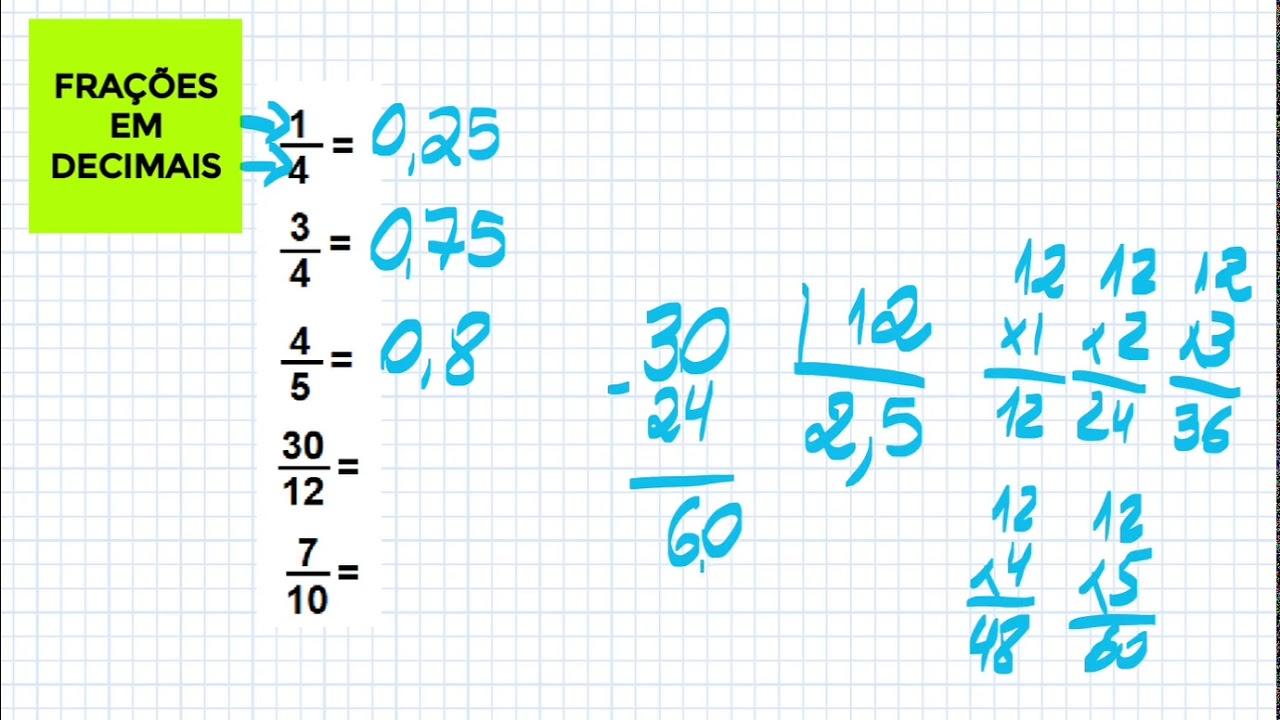
Capire quando e come una frazione si trasforma in un numero intero è il primo passo per muoversi con sicurezza tra frazioni e decimali: dalla condizione chiave “numeratore multiplo del denominatore” agli esempi pratici, tutto ruota intorno alla divisione a ÷ b e all’eventuale resto.

Allo stesso tempo, i numeri decimali e le frazioni decimali sono la lingua quotidiana delle misure, del denaro e dei calcoli: imparare a leggerli, convertirli, confrontarli ed eseguire operazioni su di essi (somme, differenze, prodotti e quozienti) rende più snelle le attività di ogni giorno, dalla spesa alle proporzioni, fino alla percentuale.

Quando una frazione diventa un numero intero

Una frazione a/b rappresenta la divisione del numeratore per il denominatore; la frazione è equivalente a un intero se e solo se a è multiplo di b. In altre parole, eseguendo a ÷ b il resto deve essere zero.

• Controllo rapido: osserva la frazione a/b e verifica se b divide a senza resto.
• Divisione: calcola a ÷ b; se il risultato non ha parte decimale, la frazione corrisponde a un intero.
• Esempio essenziale: 8/4 → 8 ÷ 4 = 2; poiché il quoziente è intero e non c’è resto, 8/4 = 2.

Questa idea è semplice ma potentissima: riconoscere i multipli del denominatore nel numeratore consente di ridurre immediatamente una frazione a un intero, evitando passaggi intermedi inutili; per approfondire vedi esempi ed esercizi risolti.

Frazioni e decimali: contesto storico e notazioni

Le frazioni non sono sempre esistite nel linguaggio matematico; si affermano quando l’uomo inizia a misurare e a rappresentare quantità non intere. Diversi popoli scelsero convenzioni differenti in base ai loro bisogni e sistemi di misura.

Gli antichi Egizi utilizzavano soprattutto le cosiddette frazioni egizie, vale a dire frazioni unitarie del tipo 1/n (come 1/2, 1/3, 1/4, 1/5, …) e decomposizioni in somme di frazioni unitarie; ad esempio, 5/6 veniva scritto come 1/2 + 1/3, una pratica con applicazioni concrete ancora oggi in alcuni contesti storici e didattici.

I Babilonesi prediligevano frazioni con denominatore 60, coerenti con il loro sistema sessagesimale, ricco di divisori; i Romani, invece, facevano ampio uso di denominatore 12, anch’esso molto “comodo” per le divisioni in parti uguali. La notazione moderna con numeratore, barra e denominatore si è consolidata solo a partire dal XVI secolo.

Per i numeri decimali, la spinta decisiva arrivò nel 1585 con Simon Stevin, che propose un metodo per eseguire i calcoli usando interi e un sistema di posizioni per indicare la parte decimale; in seguito, nel 1617, John Napier introdusse l’uso del punto o della virgola per separare parte intera e parte decimale, segnando la nascita della notazione decimale moderna.

Frazioni decimali e numeri decimali: definizioni, esempi e lettura

Una frazione decimale è una frazione con denominatore pari a una potenza di 10 (10, 100, 1000, …). Alcuni esempi: 1/10, 3/100, 23/100, 1/1000, 1/10^3. Ogni frazione decimale può essere scritta come numero decimale con virgola, separando parte intera (PI) e parte decimale (PD).

Per esempio, 127/100 = 1,27: la decomposizione mostra che 127/100 = 100/100 + 27/100 = 1 + 0,27 = 1,27. Allo stesso modo, 8/10 = 0,8: qui la parte intera è 0 e la parte decimale è 8, evidenziando che la frazione è minore di 1 poiché il numeratore è inferiore al denominatore.

Saper leggere correttamente i decimali è fondamentale. Si guarda la virgola per distinguere PI e PD e si usa il nome della posizione: decimi, centesimi, millesimi. Esempi di lettura (in italiano):

• 0,6: sei decimi.
• 0,37: trentasette centesimi.
• 0,189: centottantanove millesimi.
• 3,7: tre unità e sette decimi.
• 13,45: tredici unità e quarantacinque centesimi.
• 130,824: centotrenta unità e ottocentoventiquattro millesimi.

Ricorda anche la struttura visiva: PI, virgola, PD. Così 1/10 si scrive 0,1 con PI=0 e PD=1; e 231/100 diventa 2,31, dove la virgola separa 2 dalla parte decimale 31.

Conversioni: da frazione a decimale e da decimale a frazione

Convertire frazioni decimali in decimali è immediato: basta eseguire la divisione del numeratore per il denominatore e posizionare la virgola secondo le potenze di 10. Esempi pratici: 130/100 = 1,30; 987/1000 = 0,987; 5/1000 = 0,005.

Nel verso opposto, un decimale si trasforma in frazione decimale rimuovendo la virgola e usando come denominatore 1 seguito da tanti zeri quante sono le cifre decimali. Alcuni casi tipici: 0,5 = 5/10; 0,05 = 5/100; 2,41 = 241/100; 7,345 = 7345/1000.

Una proprietà utile: aggiungere o togliere zeri alla fine della parte decimale non cambia il valore. Per esempio, 0,5 = 0,50 = 0,500 = 0,5000; 1,0002 = 1,00020 = 1,000200; e 3,1415926535 può essere prolungato con zeri senza alterarne il valore.

Moltiplicare per potenze di 10 è altrettanto semplice: sposta la virgola a destra di tante posizioni quanti sono gli zeri (×10, ×100, ×1000 …). Esempio: 7,4 × 10 = 74; 7,4 × 100 = 740; 7,4 × 1000 = 7400.

Dividere per potenze di 10 funziona al contrario: sposta la virgola a sinistra (÷10, ÷100, ÷1000 …). Esempi: 247,5 ÷ 10 = 24,75; 247,5 ÷ 100 = 2,475; 247,5 ÷ 1000 = 0,2475.

Operazioni con numeri decimali

Addizione e sottrazione

Per sommare o sottrarre decimali è fondamentale pareggiare il numero di cifre decimali, se necessario aggiungendo zeri alla destra della parte decimale, e poi allineare le colonne (unità sotto unità, decine sotto decine, virgola sotto virgola, decimi sotto decimi, ecc.).

• Esempio di preparazione: 2,4 e 1,723 si riscrivono come 2,400 e 1,723 per allineare correttamente.
• Esempio svolto (somma con numeri dello stesso tipo): 2,400 + 1,713 = 4,113.
• Esempio svolto (differenza): 2,400 − 1,713 = 0,687.

Seguendo queste regole di allineamento, si evitano errori comuni legati alla posizione della virgola e la procedura diventa identica a quella con interi.

Moltiplicazione di decimali

Esistono due approcci equivalenti. Il primo: trasforma i decimali in frazioni decimali, moltiplica numeratore per numeratore e denominatore per denominatore e, alla fine, riporti il risultato in forma decimale. Esempio: 2,25 × 3,5 = (225/100) × (35/10) = 7875/1000 = 7,875.

Il secondo metodo: ignora provvisoriamente la virgola e moltiplica come se fossero interi; poi inserisci la virgola nel prodotto mettendo tante cifre decimali quante sono, in totale, quelle del moltiplicando più quelle del moltiplicatore (nell’esempio, 2 + 1 = 3 cifre decimali → 7,875).

Divisione di decimali

Per dividere dei decimali, una strategia efficace consiste nel eliminare le virgole moltiplicando dividendo e divisore per potenze di 10 (lo stesso fattore per entrambi), così da ottenere una divisione tra interi che produce lo stesso quoziente.

• Esempio 1: 3,6 ÷ 0,4 → moltiplica entrambi per 10: 36 ÷ 4 = 9.
• Esempio 2: 0,35 ÷ 7 → moltiplica entrambi per 100: 35 ÷ 700 = 0,05 → quoziente 0,05.

Un’applicazione concreta: una persona dona 35 unità di terreno a 700 beneficiari; ogni unità vale 24.200 m². Ognuno riceve 35/700 = 0,05 unità; moltiplicando 24.200 × 0,05 si ottengono 1.210 m² per persona.

Quando il divisore è più grande del dividendo

Consideriamo 35 ÷ 700. Il dividendo è minore del divisore, quindi si può ridimensionare la divisione moltiplicando il dividendo per una potenza di 10 (e di conseguenza il quoziente verrà diviso per la stessa potenza). Ad esempio, 35 → 3500 (×100): ora 3500 ÷ 700 = 5; riportando il fattore 100 nel quoziente, otteniamo 0,05. È lo stesso ragionamento usato poco sopra con 35 ÷ 700.

Nella pratica, questo significa che aggiungere due zeri al dividendo equivale a introdurre due cifre decimali nel quoziente (metti lo 0 e la virgola, poi prosegui), mantenendo coerente l’operazione.

Divisione di 10 per 16, passo dopo passo

La divisione 10 ÷ 16 non produce un intero. Si procede allora con la divisione in colonna introducendo decimali: 10 è minore di 16, quindi si scrive 0, e si prosegue moltiplicando il dividendo per 10 per ottenere 100 decimi.

• Prima tappa: 100 ÷ 16 = 6, resto 4.
• Seconda tappa: porta giù uno zero (40 centesimi): 40 ÷ 16 = 2, resto 8.
• Terza tappa: porta giù uno zero (80 millesimi): 80 ÷ 16 = 5, resto 0.

Il quoziente completo è 0,625. Questo esempio mostra come lavorare con decimali fino a ottenere resto zero generi un decimale esatto.

Confronto tra numeri decimali

Per confrontare due decimali, si analizzano separatamente parte intera e parte decimale utilizzando i simboli di maggioranza, minoranza o uguaglianza. Se la parte intera è diversa, il numero con parte intera maggiore è il più grande.

• Esempio con PI diverse: 4,1 > 2,76 perché 4 è maggiore di 2.
• Altro esempio: 3,7 < 5,4 perché 3 è minore di 5.

Se invece le parti intere sono uguali, si “pareggiano” le cifre decimali aggiungendo zeri dove serve, quindi si confronta la parte decimale come numero intero posizionale:

• 12,4 > 12,31 perché, scritto come 12,40 vs 12,31, si confrontano 40 e 31.
• 8,032 < 8,47 perché 8,032 < 8,470 dopo l’allineamento con gli zeri.
• 4,3 = 4,3 ovviamente, perché sia PI sia PD coincidono.

Convertire una frazione in decimale con risultato esatto: l’esempio di 3/8

Un modo molto intuitivo per passare da frazione a decimale è ricordare che a/b significa “a diviso b”. Se svolgi la divisione fino a resto zero, ottieni un decimale esatto; se il resto non si annulla, compare una parte periodica.

Prendiamo 3/8. Siccome 3 è intero, possiamo scriverlo come 3,0 o 3,00 o 3,0000… senza cambiarne il valore; questo consente di continuare la divisione oltre la virgola quando necessario. In pratica, 3 ÷ 8 equivale a 3,0000… ÷ 8, così da generare cifre decimali finché il resto diventa zero.

Svolgendo la divisione: 3 ÷ 8 = 0 con resto 3 → porta uno zero (30 decimi): 30 ÷ 8 = 3, resto 6 → porta uno zero (60 centesimi): 60 ÷ 8 = 7, resto 4 → porta uno zero (40 millesimi): 40 ÷ 8 = 5, resto 0. Il risultato è 0,375.

È lo stesso procedimento concettuale della divisione tra interi, con la differenza che non ci si ferma finché il resto non è zero (o finché riconosciamo un periodo). In questo caso, 3/8 produce un decimale finito, perché il denominatore 8 (2^3) è una potenza di 2, che è compatibile con le potenze di 10 (2 × 5).

Percentuali e proporzioni: una rapida connessione

La percentuale è una forma di rapporto in cui il denominatore è 100; cioè a/100 indica “a per cento”. Dire che in una classe il 30% sono ragazze significa: su 100 studenti ipotetici, 30 sarebbero ragazze, ovvero 30/100.

Nelle proporzioni, per calcolare ad esempio il 40% di 300, si imposta 40/100 = X/300. Il prodotto dei medi uguale al prodotto degli estremi porta a 100X = 12.000, quindi X = 120. Analogamente, se hai letto il 45% di un libro da 200 pagine, 45/100 = X/200 → 100X = 9.000 → X = 90 pagine lette; te ne restano 200 − 90 = 110.

Riconoscere quando una frazione vale un intero, trasformare frazioni in decimali (e viceversa), leggere e confrontare numeri con la virgola, e saperli sommare, sottrarre, moltiplicare e dividere ti mette nelle condizioni di affrontare con naturalezza situazioni concrete: prezzi, misure, sconti, ripartizioni e tanto altro. Con le regole viste — multipli e resti, potenze di 10, allineamento delle colonne e gestione della virgola — i passaggi diventano meccanismi affidabili, e gli esempi come 8/4 = 2, 3/8 = 0,375 o 10 ÷ 16 = 0,625 ti restano come punti di riferimento rapidi per non sbagliare.