Como dividir frações negativas sem mistério: sinais, inverso e simplificação

Início » Ciência » Matemática » Como dividir frações negativas sem mistério: sinais, inverso e simplificação

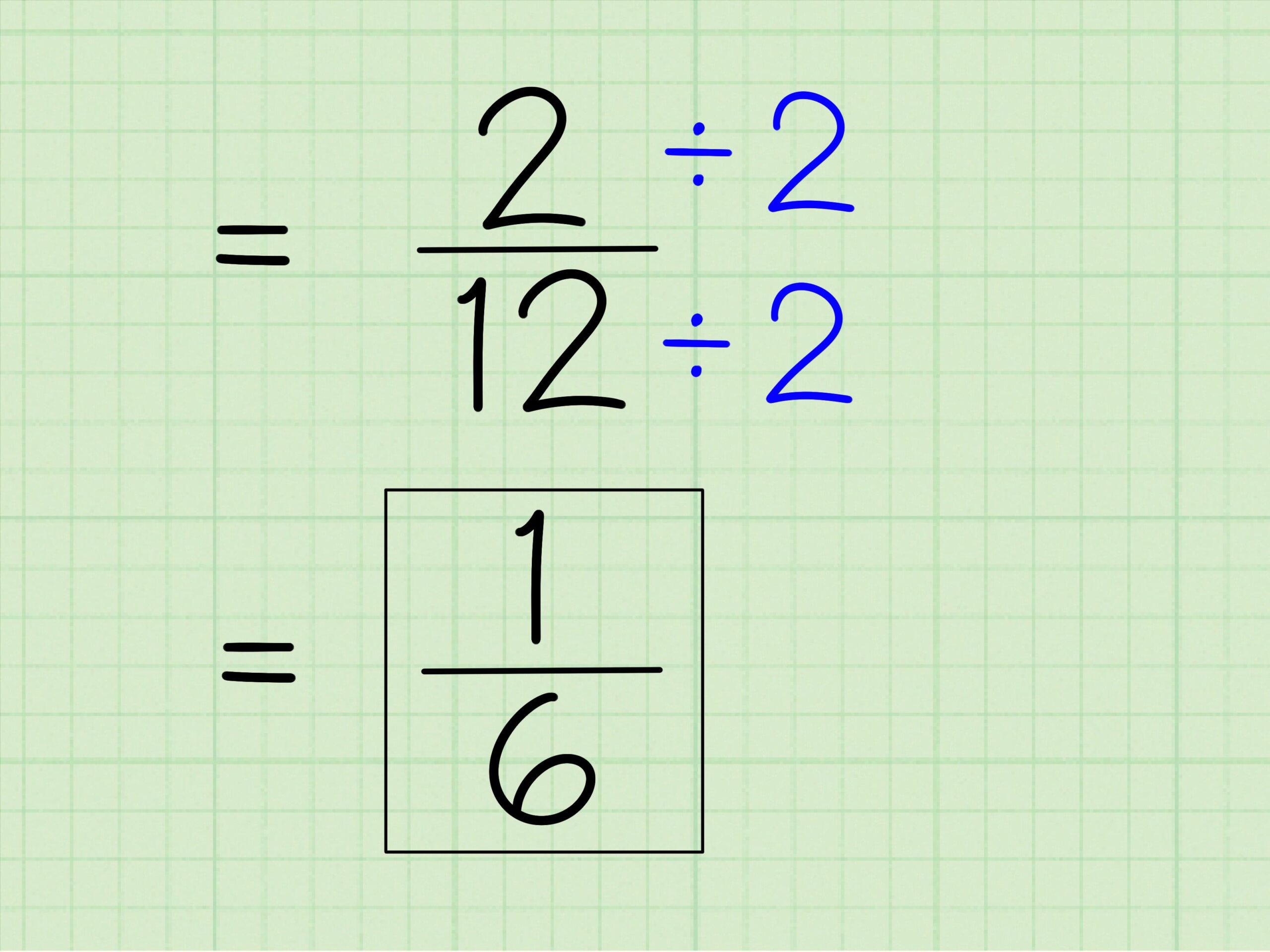
Quando o assunto é dividir frações com sinais negativos, muita gente trava por causa dos sinais e das inversões. A boa notícia é que o procedimento é enxuto e lógico: basta reinterpretar a divisão como multiplicação pelo inverso, cuidar dos sinais e, ao final, simplificar. Com um método consistente, a operação se torna automática e evita erros comuns.

Antes de colocar a mão na massa, vale lembrar que frações negativas obedecem às mesmas regras das positivas, com o detalhe adicional dos sinais. Se você dominar a regra de sinais e a ideia de “inverter a segunda fração” (o chamado inverso multiplicativo), já tem 90% do caminho andando.

O essencial sobre frações negativas

Uma fração negativa pode aparecer com o sinal no numerador, no denominador ou na frente da fração inteira: -a/b, a/(-b) e -(a/b) são equivalentes. Isso significa que o sinal “-” pode ser colocado onde for mais conveniente para o cálculo. Em geral, trazemos o sinal para a frente da fração para facilitar a leitura.

Ao dividir duas frações, a primeira recebe o nome de dividendo e a segunda, de divisor. Na divisão de frações, nunca se divide “cruzado”; em vez disso, transformamos a divisão em multiplicação pelo inverso do divisor. Essa é a grande sacada do processo.

O inverso (ou recíproco) de uma fração c/d é d/c, assumindo que c e d são diferentes de zero. Isso vale também quando há sinal: o inverso de -c/d é d/(-c). Depois que você inverte a segunda fração, a divisão vira uma multiplicação comum.

Regra de sinais na divisão de frações

Para acertar o sinal do resultado, basta lembrar das combinações possíveis. Sinais iguais (negativo com negativo, positivo com positivo) geram resultado positivo. Sinais diferentes (um positivo e outro negativo) resultam em fração negativa.

• Negativo ÷ negativo → positivo: dois sinais “-” se cancelam.
• Negativo ÷ positivo → negativo: um “-” permanece.
• Positivo ÷ negativo → negativo: novamente, um “-” permanece.
• Positivo ÷ positivo → positivo: operação usual.

Esse ajuste de sinal pode ser feito no começo (antes de inverter), no meio do cálculo ou no final. O importante é manter a coerência: conte quantos sinais “-” há no produto final. Número par de sinais negativos vira positivo; número ímpar, negativo.

Como fazer a operação na prática

O procedimento prático é direto. Em palavras, você substitui a divisão por uma multiplicação, tornando o divisor em sua forma recíproca. Em seguida, multiplica numeradores entre si e denominadores entre si, e simplifica a fração final.

Reescrevendo de forma genérica, considere (-a)/b ÷ (-c)/d, com a, b, c, d diferentes de zero. Primeiro, troque a divisão por multiplicação e inverta a segunda fração: (-a)/b × d/(-c). Multiplicando termo a termo, surgirá (-a·d)/(b·(-c)). Como há dois sinais negativos (um no numerador e outro no denominador), eles se anulam, e obtemos um resultado positivo: ad/bc.

Observe como isso espelha a regra de sinais comentada: dois negativos na divisão produzem um quociente positivo. Quando ambos os termos são negativos, o produto dos sinais é positivo, fazendo o resultado final ficar sem “-”.

Mantendo a mesma lógica, se apenas uma das frações for negativa (dividendo ou divisor), o resultado carregará um “-”. Você pode deixar esse “-” na frente do resultado ou incorporá-lo ao numerador.

Exemplos resolvidos, do básico ao avançado

Exemplo 1: (-2/3) ÷ (-4/5). Transforme em multiplicação: (-2/3) × (5/(-4)). Multiplicando, fica (-2 × 5)/(3 × -4) = (-10)/(-12). Dois sinais negativos se cancelam e o resultado é 10/12, que simplifica para 5/6.

Exemplo 2: (-7/9) ÷ (2/3). Troque por multiplicação: (-7/9) × (3/2). Resultado: (-21)/18. Agora há apenas um “-”, então o quociente é negativo: -21/18, que reduz para -7/6 (ou -1 1/6, se preferir número misto).

Exemplo 3: (5/8) ÷ (-1/4). Torne a operação em multiplicação: (5/8) × (4/(-1)) = 20/(-8). Sobra um sinal negativo, então o resultado é -20/8, que simplifica para -5/2.

Exemplo 4 (com fatoração útil): (-6/5) ÷ (-9/10). Inverta a segunda: (-6/5) × (10/(-9)). Multiplique: (-60)/(-45). Com dois negativos, fica 60/45, e podemos reduzir por 15, obtendo 4/3.

Exemplo 5 (com números mistos): -1 1/2 ÷ (-3/4). Converta para impróprias: -3/2 ÷ (-3/4). Vire a segunda: -3/2 × 4/(-3) = (-12)/(-6). Novamente, dois “-” somem e sobra 12/6, ou seja, 2.

Nesses exemplos, procure sempre simplificar no final. Se enxergar fatores comuns cedo (como um 3 que aparece em cima e embaixo), você também pode simplificar antes de multiplicar, o que reduz o tamanho dos números e evita erros de aritmética.

Por que o método funciona?

O segredo está no inverso multiplicativo: dividir por uma fração é o mesmo que multiplicar pelo número que a “desfaz” quando multiplicado por ela. Se c/d × d/c = 1, então a/b ÷ c/d precisa ser a/b × d/c. É uma consequência direta das propriedades dos números racionais.

Quanto aos sinais, usamos a regra clássica: o produto de dois números negativos é positivo. Quando a divisão vira multiplicação, estamos multiplicando os sinais envolvidos, e a contagem de sinais “-” dita o sinal do resultado.

Essa compreensão evita a memorização cega de fórmulas. Ao perceber que a divisão vira multiplicação e que sinais iguais se cancelam, você ganha autonomia para resolver qualquer caso.

Atalho seguro: simplificar antes de multiplicar

Uma estratégia que poupa tempo é reduzir fatores comuns antes da multiplicação. Por exemplo, em (8/15) ÷ (-4/9), escreva como (8/15) × (9/(-4)). Perceba que 8 e 4 dividem por 4, e 9 e 15 dividem por 3. Após cancelar: (2/5) × (3/(-1)) = 6/(-5) = -6/5.

Essa abordagem diminui o tamanho dos números e deixa a simplificação final muito mais tranquila. Quanto menos você inflar numeradores e denominadores, menor a chance de deslizes.

Erros comuns e como evitá-los

Erro 1: esquecer de inverter a segunda fração. Muita gente apenas multiplica direto e se confunde com os sinais. Lembre-se: dividir por c/d é igual a multiplicar por d/c. Sem essa inversão, o resultado sai errado.

Erro 2: trocar o sinal de lugar e perder o controle. O “-” pode ir ao numerador, ao denominador ou à frente, mas não o duplique nem o apague por acidente. Conte quantos sinais negativos há após a inversão e a multiplicação; dois negativos formam um positivo.

Erro 3: pular a simplificação. Parar em 30/42 quando dá para reduzir a 5/7, por exemplo, é desperdício e pode prejudicar comparações futuras. Sempre procure o máximo divisor comum (MDC) para simplificar.

Erro 4: confundir “dividir cruzado” com “multiplicar cruzado”. Na divisão de frações, não existe dividir cruzado; primeiro transformamos em multiplicação e só então operamos. Multiplicar cruzado é técnica de comparação de frações, não um procedimento de divisão.

Situações especiais e cuidados

Quando o numerador é zero, por exemplo, 0 ÷ (-3/5), o resultado é 0. Isso porque zero vezes qualquer número (após a inversão) continua sendo zero. Simples e seguro.

Já quando o denominador de alguma fração é zero (como 2/0), essa fração não está definida, e a divisão correspondente não faz sentido. Nunca inverta uma fração cujo numerador seja zero (0/d), pois o inverso exigiria dividir por zero.

Se houver parênteses indicando um “-” fora da fração, como -(5/7), trate-o como uma única entidade negativa. Durante a inversão da segunda fração, o sinal acompanha o numerador ou o denominador do termo invertido, sem misturar tudo.

Com números mistos, converta sempre para fração imprópria antes de qualquer passo. Esse cuidado padroniza o tratamento dos sinais e simplifica a checagem.

Verificação rápida: faz sentido o sinal e o tamanho?

Após achar o resultado, confirme duas coisas: o sinal está coerente com a regra de sinais? O tamanho (módulo) se parece razoável? Compare com um valor aproximado em decimal para sentir se você não “perdeu” o resultado.

Exemplo: (-2/3) ÷ (1/6) vira (-2/3) × 6 = -12/3 = -4. Em decimal, -0,666… dividido por 0,166… dá algo perto de -4 mesmo. Esse “teste de sanidade” é ótimo para flagrar erros.

Você também pode pensar na ideia de “quantas vezes cabe”. Se o divisor é pequeno (como 1/10), dividir por ele deve ampliar o número; se for grande (como 5), deve encolher. Essa intuição ajuda a perceber resultados fora da curva.

Aplicando o método em problemas de contexto

Imagine uma dívida representada por -3/4 de unidade e um rateio em parcelas de -1/8. Como há dois negativos, o quociente será positivo: (-3/4) ÷ (-1/8) = (-3/4) × (8/(-1)) = (-24)/(-4) = 6. Interpretação: seis parcelas do mesmo “tamanho negativo” quitariam a dívida inteira.

Em medidas e proporções, às vezes aparecemos com taxas negativas (variações abaixo de uma referência). O procedimento algébrico permanece idêntico: inverso do divisor, multiplicação e simplificação. A diferença está na leitura do sinal, que indica sentido (para cima ou para baixo, lucro ou prejuízo, ganho ou perda).

Em exercícios com grandezas físicas, tenha cuidado com zeros e denominadores. Se algum termo inviabiliza o inverso (numerador zero no divisor), a operação não é válida. Cheque a consistência do enunciado.

Do símbolo à frase: outra forma de enxergar

Escreva a operação “dividir por uma fração” como “multiplicar pelo quanto ela precisa para virar 1”. Esse “quanto” é o inverso. Quando a fração é negativa, esse “quanto” carrega o sinal respectivo, e o produto dos sinais decide o sinal final.

Assim, (-a)/b ÷ (-c)/d vira (-a)/b × d/(-c). Visualmente, um “-” está no numerador e outro no denominador do produto. Eles se neutralizam e a fração final fica positiva: (a·d)/(b·c). A mesma leitura vale para as outras combinações de sinais.

Prática guiada: exercícios comentados

(-11/12) ÷ (11/18). Inversão: (-11/12) × (18/11). Podemos simplificar 11 com 11 antes de multiplicar: sobra (-1/12) × 18/1 = -18/12. Reduzindo por 6, fica -3/2.

(3/10) ÷ (-9/5). Inversão: (3/10) × (5/(-9)). Cancelamos 5 com 10 para obter (3/2) × (1/(-9)) = 3/(-18). Resultado simplificado: -1/6.

(-4/15) ÷ (-2/9). Inversão: (-4/15) × (9/(-2)). Podemos simplificar 9 com 15 por 3: (-4/5) × (3/(-2)) = (-12)/(-10). Dois “-” se anulam: 12/10, que simplifica para 6/5.

(7/8) ÷ (-7/16). Inversão: (7/8) × (16/(-7)). Cancelamos 7 com 7: (1/8) × (16/(-1)) = 16/(-8). Fica -2.

FAQ rápido: dúvidas que sempre aparecem

Posso inverter a primeira fração? Não, quem vira de ponta-cabeça é a segunda. A divisão “a/b ÷ c/d” torna-se “a/b × d/c” exatamente porque você está “desfazendo” o divisor.

Como tratar sinais mistos como -a/(-b)? É positivo, porque há dois negativos. Em geral, traga o sinal para a frente para evitar confusão: -(a/b). Fica mais limpo e consistente.

Preciso sempre simplificar no final? Sim, é recomendável. Respostas em forma irredutível são padrão e ajudam a comparar resultados.

Existe alguma exceção ao método de inverter e multiplicar? Desde que as frações sejam válidas (sem denominador zero e com divisor não nulo), não. O procedimento é universal para números racionais.

Conectando com a regra dada em sala

Muitos materiais didáticos resumem a técnica em três orientações: substituir a divisão por multiplicação, inverter a segunda fração e simplificar. É exatamente isso o que temos feito, com a atenção extra aos sinais.

Se você pegar a forma simbólica (-a)/b ÷ (-c)/d, verá que o procedimento conduzirá a (-a)/b × d/(-c) e, depois, a (-a·d)/(b·(-c)). Como dois negativos geram positivo, o quociente final é (a·d)/(b·c), positivo, confirmando a regra.

Quer seguir além do básico? Em vez de um “clique aqui” específico, é útil consultar listas de exercícios graduados e revisões de frações e sinais. Quanto mais variados forem os enunciados, mais sólido ficará o seu domínio da técnica.

Ao colocar tudo em prática — inverter o divisor, multiplicar numeradores e denominadores e reduzir o resultado —, a divisão de frações negativas deixa de ser um bicho de sete cabeças. Com atenção aos sinais e hábito de simplificar, você ganha segurança tanto em cálculos rápidos quanto em problemas contextualizados.