Como encontrar o produto de frações: regras, sinais e exercícios

Início » Ciência » Matemática » Como encontrar o produto de frações: regras, sinais e exercícios

Encontrar o produto de frações é mais simples do que parece, e entender bem esse tema ajuda em problemas de aritmética, álgebra, porcentagens, escalas, música e muito mais. Ao contrário da soma e da subtração, na multiplicação você não precisa igualar denominadores: a regra é direta e funciona em qualquer caso.

Ao longo deste guia, você vai ver o conceito, a demonstração, as regras de sinais, truques de simplificação e muitos exemplos comentados. Também vamos cobrir casos especiais, como multiplicar fração por número inteiro e como lidar com frações mistas (as que têm parte inteira), além de exercícios resolvidos no modelo de provas e vestibulares.

O que significa o produto de frações?

Produto de frações é o resultado da multiplicação entre duas (ou mais) frações. A regra essencial é multiplicar numerador com numerador e denominador com denominador. Se temos (a/b) e (c/d), com b ≠ 0 e d ≠ 0, então: (a/b) × (c/d) = (a × c)/(b × d).

De forma prática, basta “multiplicar reto”: o número de cima pelo número de cima, e o número de baixo pelo número de baixo. Isso vale independentemente de as frações terem denominadores iguais ou diferentes.

Exemplo direto: (2/3) × (4/5) = (2 × 4)/(3 × 5) = 8/15. Note que não precisamos mexer nos denominadores para somar ou subtrair; aqui, simplesmente multiplicamos.

Outro exemplo: (1/6) × (7/3) = (1 × 7)/(6 × 3) = 7/18. Se der para simplificar no final, ótimo; se não, já está resolvido.

Passo a passo essencial (com exemplos claros)

Antes de qualquer coisa, vale recapitular os termos: o numerador é a parte de cima e indica as partes consideradas; o denominador é a parte de baixo e informa em quantas partes o todo foi dividido.

Passo 1: verifique se todas as frações estão corretas (denominadores diferentes de zero). Passo 2: multiplique numeradores entre si. Passo 3: multiplique denominadores entre si. Passo 4: se possível, simplifique o resultado para obter uma fração irredutível.

Exemplo completo: (4/9) × (3/2) = (4 × 3)/(9 × 2) = 12/18. Como 12 e 18 são múltiplos de 6, dividimos ambos por 6 e obtemos 2/3, que é a forma irredutível.

Um cuidado importante: não confunda multiplicação com adição/subtração de frações. Na soma e na subtração, repete-se o denominador quando ele é igual; já na multiplicação, multiplicamos numeradores e denominadores diretamente, mesmo que os denominadores sejam iguais.

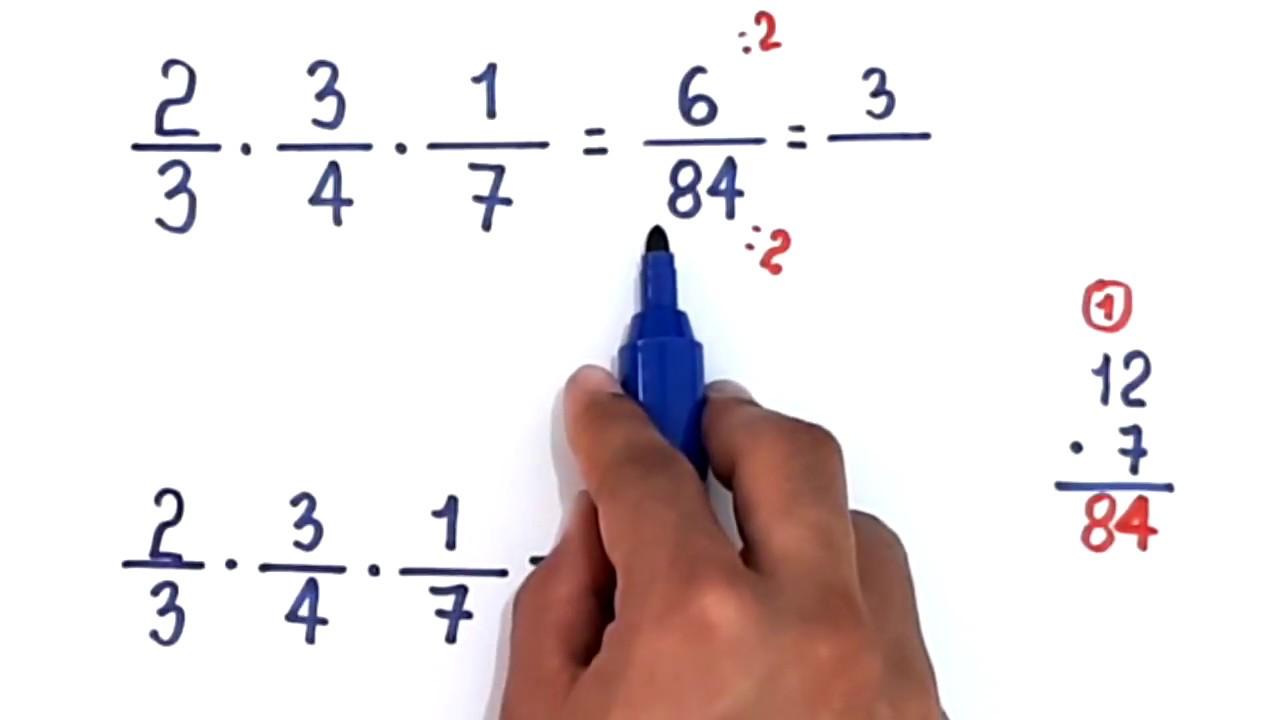
Numerador, denominador e a ideia por trás do produto

Uma fração representa uma razão entre duas grandezas; veja também os conceitos de números racionais. numerador (partes selecionadas) sobre denominador (total de partes iguais). Multiplicar frações significa compor razões: partes de partes. É por isso que a multiplicação mantém a estrutura de “cima com cima, baixo com baixo”.

Denominadores iguais ou diferentes? Tanto faz na multiplicação

Na multiplicação, não é preciso igualar denominadores. Mesmo que os denominadores sejam iguais, você continua multiplicando normalmente numeradores com numeradores e denominadores com denominadores.

Quando os denominadores coincidem, o procedimento não muda. O erro comum é aplicar a lógica da adição/subtração (em que repetimos o denominador), mas na multiplicação esse atalho não existe: o denominador final é o produto dos denominadores.

Fração por número inteiro

Para multiplicar fração por inteiro, basta lembrar que um número inteiro n pode ser escrito como n/1. Assim, (3/2) × 5 = (3 × 5)/(2 × 1) = 15/2. Outra forma prática é multiplicar o inteiro pelo numerador e manter o denominador.

Exemplos rápidos: (3/2) × 5 = 15/2 e 12 × (2/5) = (12 × 2)/5 = 24/5. Se houver chance de simplificar antes, melhor ainda (veja a seção de cancelamento).

Também é possível, em alguns contextos, dividir o inteiro pelo denominador e multiplicar pelo numerador, quando a divisão é exata, tornando a conta mais ágil. Por exemplo, 32 × (3/8) = (32 ÷ 8) × 3 = 4 × 3 = 12.

Fração mista: como multiplicar do jeito certo

Uma fração mista tem parte inteira e parte fracionária. O procedimento padrão é converter a mista em fração imprópria (numerador maior que o denominador), e só depois multiplicar.

Passos práticos: 1) transforme a mista em imprópria multiplicando o inteiro pelo denominador e somando ao numerador; 2) multiplique como em qualquer fração; 3) simplifique se possível e, se preferir, converta o resultado de volta para mista.

Exemplo: 2 1/3 × (3/4). Primeiro, 2 1/3 = (2 × 3 + 1)/3 = 7/3. Em seguida, (7/3) × (3/4) = (7 × 3)/(3 × 4) = 21/12. Dá para simplificar por 3: 7/4, que ainda pode ser escrito como 1 3/4.

Jogo de sinais: positivo ou negativo?

As frações herdam as regras de sinais dos inteiros. Sinais iguais no produto geram resultado positivo e sinais diferentes geram resultado negativo.

Exemplos: (-2/3) × (4/5) = -(8/15), pois os sinais são diferentes. Já (-1/2) × (-1/3) = 1/6, porque sinais iguais resultam em positivo.

Simplificação: depois e antes da multiplicação

Depois de multiplicar, é comum poder simplificar a fração final, encontrando frações equivalentes. Isso acontece quando numerador e denominador têm divisores comuns. Exemplo: (4/9) × (3/2) = 12/18; dividindo ambos por 6, obtemos 2/3, que é irredutível.

Entretanto, existe um truque que acelera muito a conta: simplificar antes de multiplicar. Esse processo recebe nomes como “cancelamento” ou “eliminação de fatores comuns”.

Eliminação de fatores iguais

Se um fator aparece no numerador de uma fração e no denominador da outra, podemos cancelá-lo, pois dividir pelo mesmo número em cima e embaixo não altera o valor da expressão. Exemplo: (9/7) × (8/9) = 8/7, pois os 9 se cancelam.

Método do cancelamento (simplificação antecipada)

No cancelamento, também podemos simplificar múltiplos antes da multiplicação. Exemplo: (9/5) × (15/6). Divida 15 e 5 por 5: vira (9/1) × (3/6). Em seguida, divida 9 e 6 por 3: vira (3/1) × (3/2). Agora multiplique: 9/2. O mesmo resultado seria obtido multiplicando primeiro (135/30) e simplificando por 15, mas adiantar a simplificação deixa tudo mais rápido.

Erros comuns e boas práticas

Erro 1: tentar igualar denominadores na multiplicação. Isso vale para soma e subtração, não para o produto.

Erro 2: esquecer o jogo de sinais. Sinais diferentes geram resultado negativo, e iguais, positivo. Cheque o sinal antes de finalizar.

Erro 3: pular a simplificação. Verifique sempre se dá para reduzir a fração ao final ou antecipar a simplificação pelo cancelamento.

Boa prática: quando possível, simplifique antes de multiplicar. Isso evita números grandes e reduz a chance de erro.

Divisão de frações (conexão útil com o produto)

A divisão entre frações se transforma em multiplicação: multiplica-se pela fração inversa. Exemplo: (a/b) ÷ (c/d) = (a/b) × (d/c). Embora o foco aqui seja o produto, entender essa relação ajuda em problemas mistos.

Exemplo rápido: (3/5) ÷ (2/3) = (3/5) × (3/2) = 9/10. A estrutura segue todas as regras de simplificação e sinais vistas acima.

Exercícios resolvidos passo a passo

Questão 1 — Efetue a multiplicação e escreva o inverso do resultado: (2/5) × (5/3). Solução: (2 × 5)/(5 × 3) = 10/15 = 2/3. O inverso de 2/3 é 3/2.

Questão 2 — Em uma coleção com 12 esmaltes, 2/3 são da marca Alfa. Quantos são Alfa? Cálculo: 12 × (2/3) = 8. Logo, a quantidade é 8.

Questão 3 — Em um mapa, 1 cm representa 5 km. Se a distância entre A e B é de 12 cm no desenho, qual é a distância real? Basta multiplicar: 12 × 5 = 60 km. Interpretamos 12 × (5/1) = 60.

Questão 4 — Calcule (9/5) × (15/6) e dê a fração irredutível. Multiplicando: (9 × 15)/(5 × 6) = 135/30. Simplificando por 15, temos 9/2. Se houvesse alternativas, escolheríamos a opção 9/2.

Questão 5 (Música) — Um trecho de oito compassos com fórmula 3/4 deve totalizar 8 × (3/4) = 6 unidades de tempo. Verificando possibilidades, uma combinação válida é 24 colcheias e 12 semínimas, pois 24 × (1/8) + 12 × (1/4) = 3 + 3 = 6.

Questão 6 — O produto entre as razões x/4 e 5/2 é 30. Encontre x. Montando: (x/4) × (5/2) = 30 → (5x)/8 = 30 → 5x = 240 → x = 48. Sempre que possível, confira se dá para simplificar no meio do caminho.

Questão 7 — Multiplicação com sinais: (-2/3) × (4/5). Como os sinais são diferentes, o resultado é negativo: (2 × 4)/(3 × 5) = 8/15, então -(8/15).

Questão 8 — Fração mista: 1 2/5 × (5/6). Primeiro, 1 2/5 = (1 × 5 + 2)/5 = 7/5. Produto: (7/5) × (5/6) = (7 × 5)/(5 × 6) = 7/6. Se quiser, escreva como 1 1/6.

Quando vale acelerar com cancelamento

Se você enxerga fatores comuns cruzados, simplifique antes. Isso reduz o tamanho dos números e dos cálculos, com menos risco de se confundir.

Exemplo prático: (12/20) × (15/18). Simplifique 12/20 por 4 → 3/5. Simplifique 15/18 por 3 → 5/6. Agora: (3/5) × (5/6) = 15/30 = 1/2. Note que deu para cancelar o 5 também, se feito cruzado: 3/5 × 5/6 → 3/6 = 1/2.

Outro exemplo curto: (14/21) × (9/6). 14/21 simplifica por 7 → 2/3; 9/6 simplifica por 3 → 3/2. Em seguida: (2/3) × (3/2) = 6/6 = 1. Rápido e sem inflar números.

Casos clássicos para treinar o olhar

1) Inteiro com fração que divide “certinho”: 32 × (3/8). Divida o inteiro pelo denominador (se possível) e multiplique pelo numerador: 32 ÷ 8 = 4 → 4 × 3 = 12.

2) Produto de várias frações: (2/3) × (9/4) × (1/6). Cancelando 3 com 9 → vira 1 e 3; cancelando 2 com 4 → vira 1 e 2; cancelando 3 com 6 → vira 1 e 2. Ao final, 1/(2 × 2) = 1/4. O cancelamento bem feito limpa a expressão.

3) Denominadores iguais: (5/7) × (3/7). Mesmo com denominadores iguais, não some ou repita denominador; multiplique: 15/49 e veja se há simplificação (aqui não há).

Perguntas frequentes rápidas

Preciso igualar denominadores? Não, só multiplique numeradores e denominadores. Igualar denominadores só se aplica a soma e subtração.

Posso simplificar no meio da conta? Sim, e é recomendável. Cancelar fatores comuns antes da multiplicação deixa os cálculos menores.

E se o resultado não simplifica? Sem problema, a fração já está irredutível e o produto está correto.

Como lido com sinais? O mesmo jogo dos inteiros: sinais iguais dão positivo; diferentes, negativo.

Dominar o produto de frações abre caminho para temas como porcentagens, escalas e expressões algébricas; quando você internaliza a regra “numerador com numerador, denominador com denominador”, a conta flui. Some a isso o cancelamento inteligente, a atenção aos sinais e a capacidade de simplificar no final, e você terá um método rápido, seguro e versátil para qualquer contexto.