Multiplicação de frações: regra, sinais, simplificação e exercícios

Início » Ciência » Matemática » Multiplicação de frações: regra, sinais, simplificação e exercícios

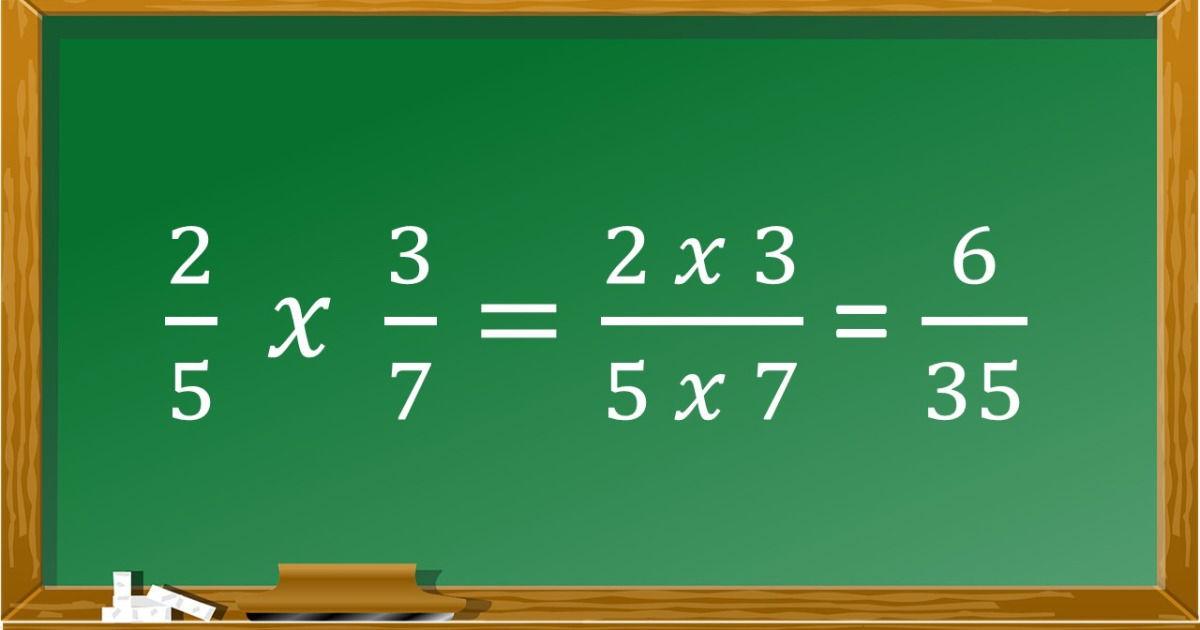
A multiplicação de frações é uma habilidade essencial em Matemática, presente em problemas do dia a dia, em provas e em conteúdos mais avançados. Aqui você vai descobrir que multiplicar frações é direto: numerador com numerador e denominador com denominador, sem a necessidade de igualar denominadores como acontece na adição e na subtração.

Neste guia completo você encontrará explicações passo a passo, regras de sinais, técnicas de simplificação e exercícios resolvidos (incluindo questões de estilo ENEM e aplicações práticas). A ideia é apresentar tudo de forma clara e natural, com dicas para ganhar velocidade e evitar os erros mais comuns.

O que é e como funciona a multiplicação de frações

Uma fração é formada por numerador (parte de cima) e denominador (parte de baixo). O numerador indica quantas partes estamos considerando, enquanto o denominador mostra em quantas partes o todo foi dividido.

Para multiplicar frações, basta multiplicar “reto”: numerador da primeira pelo numerador da segunda e denominador da primeira pelo denominador da segunda. Essa regra vale para duas ou mais frações.

Forma geral: se a/b e c/d são frações (com b ≠ 0 e d ≠ 0), então a/b × c/d = (a × c)/(b × d).

Exemplos diretos: 2/3 × 4/5 = 8/15; 1/6 × 7/3 = 7/18. Em ambos os casos, multiplicamos numeradores entre si e denominadores entre si.

Importante: multiplicação de frações não exige denominadores iguais; essa exigência é exclusiva da soma e da subtração de frações.

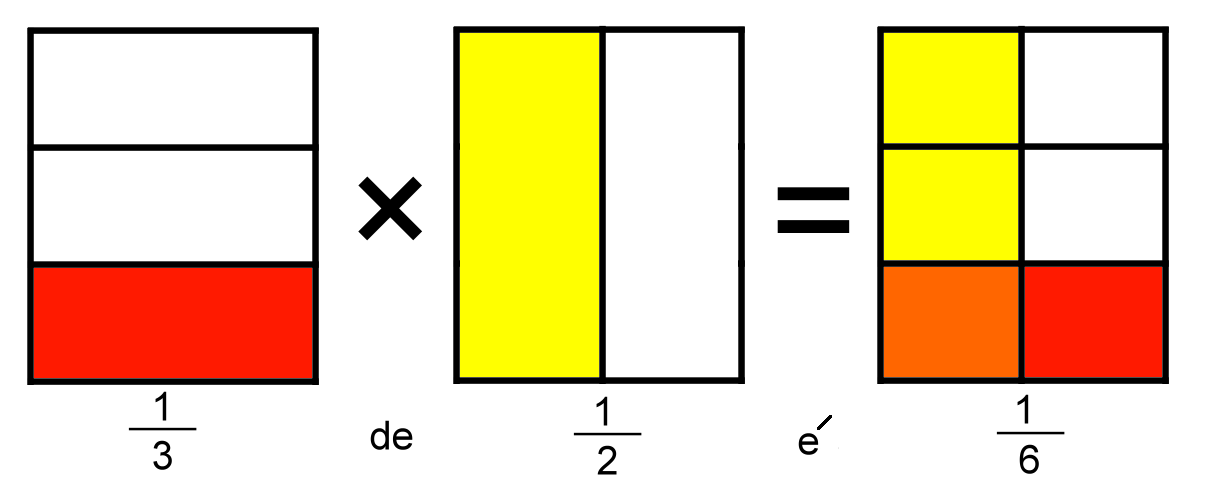
Multiplicação de fração por número inteiro

Quando multiplicamos uma fração por um número inteiro, consideramos esse inteiro com denominador 1. Assim, o denominador da fração é mantido e multiplicamos o inteiro pelo numerador.

Exemplos práticos: 3/2 × 5 = (3 × 5)/2 = 15/2; 12 × 2/5 = (12 × 2)/5 = 24/5. Note que tratamos 5 como 5/1 e 12 como 12/1.

Aplicação cotidiana: se um pote tem 3/4 kg de achocolatado e temos 8 potes iguais, então 8 × 3/4 = 24/4 = 6 kg. É a mesma lógica da multiplicação por inteiro.

Frações com denominadores iguais e diferentes

Mesmo que os denominadores sejam iguais, ainda assim multiplicamos numeradores com numeradores e denominadores com denominadores. Não há “repetição do denominador” como ocorre em soma/subtração.

Exemplo (denominadores iguais): 2/7 × 5/7 = (2 × 5)/(7 × 7) = 10/49. Repare que o denominador foi multiplicado por 7 × 7.

Exemplo (denominadores diferentes): 1/6 × 7/3 = (1 × 7)/(6 × 3) = 7/18. Não precisamos torná-los iguais.

Alerta: é muito comum confundir com a regra da adição de frações; na multiplicação, você nunca soma ou iguala denominadores.

Frações mistas: como multiplicar

Fração mista possui uma parte inteira e uma parte fracionária (por exemplo, 2 1/3). Para multiplicar uma fração mista por outra fração, primeiro converta a mista em fração imprópria (numerador maior que o denominador).

Passo a passo: 1) transforme a fração mista em imprópria; 2) multiplique as frações pelo método padrão (numerador com numerador e denominador com denominador).

Exemplo: 1 1/2 × 2/3. Converta 1 1/2 em 3/2. Depois: 3/2 × 2/3 = (3 × 2)/(2 × 3) = 6/6 = 1.

Dica: ao final, se desejar, converta o resultado em fração mista novamente (quando fizer sentido), mas isso não é obrigatório.

Regras de sinais na multiplicação de frações

As frações seguem o mesmo jogo de sinais dos inteiros: produto de sinais iguais resulta em positivo; produto de sinais diferentes resulta em negativo.

Exemplos com sinais: (−2/3) × 4/5 = −8/15; (−1/2) × (−1/3) = 1/6. O cálculo numérico é o mesmo; a diferença está no sinal do produto.

Boa prática: determine o sinal do resultado antes de multiplicar os termos, pois isso ajuda a não errar no fim.

Simplificação e fração irredutível

Depois de multiplicar, verifique se numerador e denominador possuem divisores comuns. Se houver, simplifique dividindo ambos pelo mesmo número até não ser mais possível. O resultado final, quando não dá para reduzir, é chamado de fração irredutível.

Exemplo: 4/9 × 3/2 = (4 × 3)/(9 × 2) = 12/18. Como 12 e 18 têm divisores comuns (2, 3 e 6), dividindo ambos por 6 encontramos 2/3.

Equivalência: frações como 12/18 e 2/3 são equivalentes; representam a mesma quantidade, ainda que em “formatos” diferentes. Para aprofundar, veja frações equivalentes.

Técnicas para multiplicar mais rápido

Existem dois atalhos que economizam tempo e evitam números grandes: a eliminação de fatores iguais e o método do cancelamento (simplificação antes de multiplicar).

Eliminação de fatores iguais

Quando o mesmo número aparece no numerador de uma fração e no denominador da outra, podemos “eliminá-lo” dividindo ambos por ele mesmo (equivale a simplificar por esse fator).

Exemplo: 9/7 × 8/9. O 9 aparece no numerador da primeira e no denominador da segunda; cancelando 9 com 9, sobra 1 no lugar deles: 1/7 × 8/1 = 8/7.

Sem eliminar, faríamos 9/7 × 8/9 = (9 × 8)/(7 × 9) = 72/63 e depois simplificaríamos, o que dá mais trabalho.

Método do cancelamento (simplificar antes de multiplicar)

Também é possível simplificar cruzado, dividindo numeradores e denominadores por fatores comuns antes de efetuar o produto.

Exemplo: 5/12 × 9/5. Cancelamos os 5, substituindo por 1. Depois, simplificamos 9 e 12 dividindo ambos por 3: 9 → 3 e 12 → 4. Resultado direto: 1/4 × 3/1 = 3/4.

Sem cancelamento prévio: 5/12 × 9/5 = (45)/(60) e então simplificamos por 15, chegando a 3/4. O cancelamento antecipado torna tudo mais rápido.

Cuidados e erros comuns

Erro clássico: confundir multiplicação com adição de frações. Na multiplicação, nunca somamos denominadores e não precisamos torná-los iguais.

Outra armadilha: esquecer de simplificar o resultado quando possível. A forma irredutível é preferível em respostas finais, especialmente em provas.

Organização ajuda: determine o sinal do produto, verifique oportunidades de cancelamento e só então multiplique. Essa sequência reduz erros.

Aplicações práticas do cotidiano

Escalas e mapas: se cada 1 cm no mapa representa 5 km na realidade, então 12 cm correspondem a 12 × 5 = 60 km. Aqui a multiplicação por uma fração (ou razão) traduz a proporcionalidade.

Receitas e medidas: dobrar “meias porções” ou multiplicar quantidades fracionárias de ingredientes é um uso direto do produto de frações.

Probabilidade e estatística: ao combinar eventos proporcionais, multiplicamos frações/razões para encontrar porções do todo de forma cumulativa.

Exemplos resolvidos passo a passo

Exemplo 1 — Produto simples e forma irredutível

Calcule 9/5 × 15/6 e escreva na forma irredutível. Produto: (9 × 15)/(5 × 6) = 135/30. Simplificando por 15: 9/2. Portanto, a forma irredutível é 9/2.

Exemplo 2 — Multiplicação por inteiro

Um pote tem 3/4 kg de achocolatado e há 8 potes iguais. Cálculo: 8 × 3/4 = (8 × 3)/4 = 24/4 = 6. Assim, são 6 kg ao todo.

Exemplo 3 — Composição em duas etapas (sala de aula)

Em uma turma, 2/3 dos alunos são meninas e, dentre elas, 3/4 têm cabelo castanho. Porcentagem da turma com cabelo castanho: 2/3 × 3/4 = 6/12 = 1/2. Metade da sala tem cabelo castanho.

Exemplo 4 — Questão de ritmo musical (estilo ENEM)

Um trecho musical tem oito compassos, cada qual com fórmula 3/4. Total: 8 × 3/4 = 24/4 = 6 unidades de tempo. Verificando combinações possíveis, uma composição com 24 colcheias e 12 semínimas soma 6 unidades (24 × 1/8 + 12 × 1/4 = 3 + 3 = 6).

Exemplo 5 — Fração de fração (chocolate)

Havia 1/3 de uma barra de chocolate e alguém comeu metade disso. Resultado: 1/3 × 1/2 = 1/6 da barra de chocolate.

Exemplo 6 — Distância em mapa

Na escala 1 cm → 5 km, a distância no mapa entre as cidades é 12 cm. Distância real: 12 × 5 = 60 km.

Exemplo 7 — Inverso do resultado

Efetue 2/3 × 3/5 e informe o inverso do produto. Produto: (2 × 3)/(3 × 5) = 6/15 = 2/5 (irredutível). O inverso (recíproco) de 2/5 é 5/2.

Mais exemplos comentados

Multiplicações diretas: 2/3 × 4/5 = 8/15; 1/6 × 7/3 = 7/18. Quando possível, confira se dá para simplificar ao final.

Com sinais: (−2/3) × 4/5 = −8/15; (−1/2) × (−1/3) = 1/6. Sinais iguais dão positivo; diferentes, negativo.

Cancelamento “na veia”: 9/7 × 8/9 = 8/7, cancelando 9. Essa técnica reduz contas desnecessárias.

De mista para imprópria: 2 1/3 × 3/4 = (7/3) × 3/4 = 21/12 = 7/4 (após simplificar por 3). O processo sempre passa pela conversão.

Checklist rápido para multiplicar frações

Antes de começar, vale uma mini-rotina mental: 1) defina o sinal do produto; 2) veja se há cancelamentos (fatores iguais ou divisíveis) possíveis; 3) multiplique numeradores e denominadores; 4) simplifique o resultado.

• Identifique fatores comuns e simplifique antecipadamente para facilitar.
• Evite confundir regras: multiplicar não é somar frações.
• Prefira a forma irredutível na resposta final.

Com prática, o processo fica automático e mais rápido, e você ganha segurança para lidar com várias frações, inclusive em situações com números negativos, mistas e aplicações de escala.

Multiplicar frações resume-se a uma regra simples acompanhada de bons hábitos: conferir sinais, simplificar sempre que puder e aplicar a técnica com atenção ao que é pedido no problema.