Um hipercubo, também conhecido como tesseract, é uma figura geométrica tridimensional generalizada para quatro ou mais dimensões. Ele é a versão multidimensional de um cubo e possui características únicas que desafiam a nossa compreensão espacial. As dimensões de um hipercubo representam o número de coordenadas necessárias para descrever a sua localização em um espaço n-dimensional. Além disso, um hipercubo pode ser dividido em seções menores, chamadas de subcubos, que mantêm a mesma forma e proporção do hipercubo original. Este fascinante objeto matemático tem sido objeto de estudo e exploração em diversas áreas da matemática e da física.
Descubra a incrível geometria de um hipercubo e seu impacto no espaço tridimensional.
O hipercubo, também conhecido como tesseract, é uma figura geométrica tridimensional que se estende para quatro dimensões. Enquanto nós vivemos em um mundo tridimensional, o hipercubo desafia nossa percepção convencional de espaço e geometria.
Um hipercubo é formado por oito cubos iguais conectados em cada vértice. Cada cubo está perpendicular aos outros, criando uma estrutura complexa e fascinante. Em termos matemáticos, um hipercubo possui 16 vértices, 32 arestas, 24 faces e 8 células.
Para descrever um hipercubo em um sistema de coordenadas, cada vértice pode ser representado por um conjunto de quatro coordenadas (x, y, z, w). Essas coordenadas descrevem a posição de cada vértice no espaço tridimensional, assim como a quarta dimensão que o hipercubo incorpora.
Uma maneira interessante de visualizar um hipercubo é através da sua projeção no espaço tridimensional. Ao projetar um hipercubo em nosso mundo tridimensional, podemos observar formas intrigantes e simétricas que desafiam nossa compreensão tradicional de geometria.
A divisão de um hipercubo em suas partes constituintes revela a complexidade e a beleza da geometria de quatro dimensões. Cada face, aresta e vértice interage de maneira única, criando uma estrutura matemática única e surpreendente.
Em suma, o hipercubo é uma figura geométrica fascinante que nos desafia a explorar novas dimensões e expandir nossa compreensão do espaço. Sua incrível geometria e impacto no espaço tridimensional nos convidam a contemplar a complexidade e a beleza do universo matemático.
Número de lados presente em um hipercubo de forma geométrica tridimensional.
Um hipercubo, também conhecido como tesseract, é uma forma geométrica tridimensional que faz parte da família dos polítopos. Ele é a projeção tridimensional de um cubo em quatro dimensões. O hipercubo possui 8 vértices, 24 arestas, 32 faces e 16 células.
Em relação ao número de lados presentes em um hipercubo, podemos calcular de forma simples. Cada vértice está conectado a 4 arestas, cada aresta está conectada a 4 vértices e a 4 faces, cada face está conectada a 4 arestas e a 4 células, e cada célula está conectada a 4 faces. Portanto, somando os lados de todas essas conexões, chegamos ao total de 80 lados em um hipercubo.
Para visualizar um hipercubo, podemos representá-lo utilizando coordenadas. Por exemplo, um hipercubo unitário pode ser representado pelas coordenadas (±1, ±1, ±1, ±1). A partir dessas coordenadas, podemos dividir o hipercubo em regiões menores, como hiperparalelepípedos, e explorar suas propriedades geométricas.
Qual é o tamanho de um cubo e qual sua dimensão?
Um cubo é um poliedro com seis faces quadradas congruentes. Ele possui todas as arestas com o mesmo comprimento e todos os ângulos retos. O tamanho de um cubo é determinado pela medida da aresta, que é a distância entre dois vértices opostos. Por exemplo, se a aresta de um cubo mede 5 unidades, então o tamanho do cubo é 5 unidades.
A dimensão de um cubo é tridimensional, o que significa que ele tem três dimensões: comprimento, largura e altura. Essas dimensões são representadas pelos eixos x, y e z em um sistema de coordenadas tridimensional.
Um hipercubo, por outro lado, é uma generalização do conceito de cubo para um número maior de dimensões. Enquanto um cubo é tridimensional, um hipercubo pode ter qualquer número de dimensões. Por exemplo, um hipercubo de quatro dimensões é chamado de tesseract, enquanto um hipercubo de cinco dimensões é chamado de penteract.
As coordenadas de um hipercubo são representadas por um vetor com um número correspondente de componentes. Por exemplo, as coordenadas de um hipercubo tridimensional são representadas por um vetor com três componentes (x, y, z).
Um hipercubo pode ser dividido em subcubos menores de dimensões inferiores. Por exemplo, um tesseract (hipercubo de quatro dimensões) pode ser dividido em cubos tridimensionais, que por sua vez podem ser divididos em quadrados bidimensionais.
Um hipercubo é uma generalização do conceito de cubo para um número maior de dimensões, e pode ser dividido em subcubos menores de dimensões inferiores.
Diferenças entre cubo e hipercubo: entenda as características dessas figuras geométricas tridimensionais.
Hipercubo: Definição, dimensões, coordenadas, divisão
O hipercubo é uma figura geométrica tridimensional que se difere do cubo em várias características. Enquanto o cubo é uma figura tridimensional com seis faces quadradas idênticas, o hipercubo é uma extensão dessa ideia para mais dimensões. No caso do hipercubo, estamos falando de uma figura geométrica que possui mais de três dimensões, sendo comumente representada como um cubo dentro de outro cubo.
As dimensões do hipercubo variam de acordo com o número de lados que ele possui. Enquanto um cubo tradicional possui três dimensões (comprimento, largura e altura), um hipercubo pode ter quatro dimensões, cinco dimensões e assim por diante. Isso significa que um hipercubo é uma figura geométrica mais complexa e abstrata do que um simples cubo.
As coordenadas de um hipercubo também são mais complexas do que as de um cubo. Enquanto um cubo pode ser representado por três coordenadas (x, y, z), um hipercubo pode necessitar de mais coordenadas para descrever sua posição no espaço. Isso reflete a maior quantidade de dimensões que um hipercubo possui em comparação com um cubo.
A divisão de um hipercubo também é mais complexa do que a divisão de um cubo. Enquanto um cubo pode ser dividido em seis faces quadradas, um hipercubo pode ser dividido em uma quantidade maior de faces, dependendo do número de dimensões que ele possui. Essa divisão mais complexa reflete a natureza abstrata e multidimensional do hipercubo.
Hipercubo: definição, dimensões, coordenadas, divisão
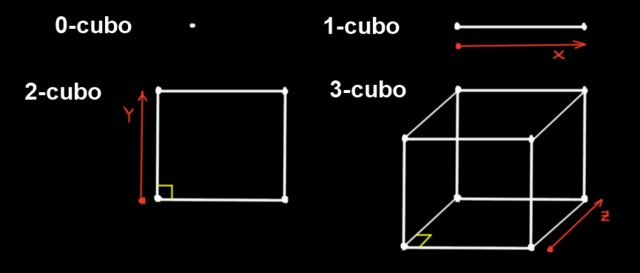
Um hipercubo é um cubo de dimensão n. O caso particular do hipercubo quadridimensional é chamado teseracto . Um hipercubo ou cubo n consiste em segmentos retos, todos de igual comprimento, ortogonais em seus vértices.
Os seres humanos percebem o espaço tridimensional: largura, altura e profundidade, mas não é possível visualizar um hipercubo com dimensão maior que 3.
No máximo, podemos fazer projeções dele no espaço tridimensional para representá-lo, semelhante à maneira como projetamos um cubo em um plano para representá-lo.
Na dimensão 0, a única figura é o ponto; portanto, um cubo 0 é um ponto. Um cubo 1 é um segmento reto, formado por mover um ponto em uma direção a uma distância a.
Por seu lado, um cubo 2 é um quadrado. É construído movendo o cubo 1 (o segmento longo a) na direção y, ortogonal à direção x, a uma distância a.
O cubo 3 é o cubo comum. Ele é construído a partir do quadrado movendo-o na terceira direção (z), ortogonal às direções xey, a uma distância a .
O 4-cubo é o tesseracto, o qual é construído a partir de um 3-cubo movendo-ortogonal, uma distância de , no sentido de uma quarta dimensão (ou quarta direcção), o qual não pode perceber.
Um tesserato tem todos os seus ângulos retos, possui 16 vértices e todas as suas arestas (18 no total) têm o mesmo comprimento a .
Se o comprimento das arestas de um cubo n ou hipercubo de dimensão n for 1, é um hipercubo unitário, no qual a diagonal mais longa mede √n.
Quais são as dimensões?
As dimensões são graus de liberdade ou as possíveis direções nas quais um objeto pode ser movido.
Na dimensão 0, não há possibilidade de movimento e o único objeto geométrico possível é o ponto.
Uma dimensão no espaço euclidiano é representada por uma linha ou eixo orientado que define essa dimensão, chamada eixo X. A separação entre dois pontos A e B é a distância euclidiana:
d = √ [(x a – x b ) 2 ].
Em duas dimensões, o espaço é representado por duas linhas orientadas ortogonais entre si, chamadas eixo X e eixo Y.
A posição de qualquer ponto neste espaço bidimensional é dada por seu par de coordenadas cartesianas (x, y) e a distância entre quaisquer dois pontos A e B será:
d = √ [(x a – x b ) 2 + (y a – y b ) 2 ]
Porque é um espaço onde a geometria de Euclides é cumprida.
Espaço tridimensional
Espaço tridimensional é o espaço em que nos movemos. Ele tem três direções: largura, altura e profundidade.
Em uma sala vazia, os cantos perpendiculares entre si dão essas três direções e para cada uma podemos associar um eixo: X, Y, Z.
Esse espaço também é euclidiano e a distância entre dois pontos A e B é calculada da seguinte forma:
d = √ [(x a – x b ) 2 + (y a – y b ) 2 + (z a – z b ) 2 ]
Os seres humanos não podem perceber mais de três dimensões espaciais (ou euclidianas).
No entanto, do ponto de vista estritamente matemático, é possível definir um espaço euclidiano n-dimensional.
Nesse espaço, um ponto possui coordenadas: (x1, x2, x3,… .., xn) e a distância entre dois pontos é:
d = √ [(x 1a – x 1b ) 2 + (x 2a – x 2b ) 2 +… .. + (x na – x nb ) 2 ].
A quarta dimensão e tempo
De fato, na teoria da relatividade, o tempo é tratado como mais uma dimensão e uma coordenada é associada a ele.
Mas deve ser esclarecido que essa coordenada associada ao tempo é um número imaginário. Portanto, a separação de dois pontos ou eventos no espaço-tempo não é euclidiana, mas segue a métrica de Lorentz.
Um hipercubo quadridimensional (o tesserato) não vive no espaço-tempo, pertence a um hiperespaço euclidiano quadridimensional.
As coordenadas de um hipercubo
As coordenadas dos vértices de um cubo n centrado na origem são obtidas fazendo todas as permutações possíveis da seguinte expressão:
(a / 2) (± 1, ± 1, ± 1,…., ± 1)
Onde a é o comprimento da aresta.
-O volume de um n-cubo da aresta a é: (a / 2) n (2 n ) = a n .
-A diagonal mais longa é a distância entre os vértices opostos.
-Os seguintes são vértices opostos em um quadrado : (-1, -1) e (+1, +1).
-E em um cubo : (-1, -1, -1) e (+1, +1, +1).
-A diagonal mais longa de um n-cubo mede:
d = √ [1 – (- 1)) 2 + … + (1 – (- 1)) 2 ] = √ [n 2 2 ] = 2√n
Nesse caso, assumiu-se que o lado é a = 2. Para um n-cubo, qualquer um será:
d = a√n.
-Um tesseract possui cada um de seus 16 vértices conectados a quatro arestas. A figura a seguir mostra como os vértices são conectados em um tesseract.
Desdobramento de um hipercubo
Uma figura geométrica regular, por exemplo, um poliedro, pode ser dividida em várias figuras dimensionais menores.
No caso de um cubo 2 (um quadrado), ele pode ser dividido em quatro segmentos, ou seja, quatro cubos 1.
Da mesma forma, um cubo 3 pode ser dividido em seis 2 cubos.
Um cubo de 4 (tesseract) pode ser dividido em oito 3 cubos.
A animação a seguir mostra o desenvolvimento de um tesseract.
Referências
- Cultura científica. Hipercubo, visualizando a quarta dimensão. Recuperado de: culturacientifica.com
- Epsilones. Hipercubo tetradimensional ou tesserato. Recuperado de: epsilones.com
- Perez R, Aguilera A. Um método para obter um tesserato a partir do desenvolvimento de um hipercubo (4D). Recuperado de: researchgate.net
- Wikilivros. Matemática, Poliedros, Hipercubos. Recuperado de: es.wikibooks.org
- Wikipedia. Hypercube. Recuperado de: en.wikipedia.com
- Wikipedia. Tesseract. Recuperado de: en.wikipedia.com