Um gráfico poligonal é uma representação visual de dados que utiliza linhas para conectar pontos em um plano cartesiano. Ele é frequentemente utilizado para mostrar mudanças ao longo do tempo ou comparações entre diferentes variáveis. Os pontos são plotados em um eixo horizontal e vertical, e as linhas são desenhadas para conectar os pontos, formando assim um polígono.
Um exemplo comum de gráfico poligonal é o gráfico de linha, que mostra a evolução de uma variável ao longo do tempo. Outro exemplo é o gráfico de dispersão, que mostra a relação entre duas variáveis através da conexão de pontos no plano cartesiano. Esses gráficos são importantes ferramentas de análise de dados e facilitam a compreensão visual das informações apresentadas.
Conheça os diferentes tipos de gráficos utilizados para representar dados de forma visual.
Um dos tipos de gráficos utilizados para representar dados de forma visual é o gráfico poligonal. Este tipo de gráfico é composto por uma série de pontos conectados por segmentos de reta, formando uma linha que mostra a evolução de uma variável ao longo do tempo ou de acordo com uma determinada categoria.
Os gráficos poligonais são úteis para visualizar tendências e padrões nos dados, facilitando a compreensão das informações de forma rápida e intuitiva. Eles são frequentemente utilizados em áreas como estatística, economia, ciências sociais e marketing.
Um exemplo de gráfico poligonal é o gráfico de linha, que mostra a evolução de uma variável ao longo do tempo. Por exemplo, um gráfico de linha pode representar a variação da temperatura ao longo dos meses do ano, permitindo visualizar se há alguma tendência de aumento ou queda.
Em resumo, os gráficos poligonais são uma ferramenta poderosa para representar dados de forma visual, facilitando a análise e interpretação das informações. Eles são amplamente utilizados em diversas áreas e podem ser uma forma eficaz de comunicar resultados de forma clara e objetiva.
Entenda a função de um gráfico na representação visual de dados estatísticos.
Os gráficos são ferramentas essenciais na representação visual de dados estatísticos, pois permitem uma visualização mais clara e rápida das informações. Eles facilitam a compreensão dos dados, tornando mais fácil identificar padrões, tendências e relações entre variáveis. Além disso, os gráficos são úteis para comunicar informações de forma mais eficaz, tornando a apresentação dos dados mais atrativa e acessível.
Um gráfico poligonal é um tipo de gráfico que representa a relação entre duas variáveis por meio de segmentos de reta que se unem formando uma linha. Esse tipo de gráfico é útil para mostrar a evolução de dados ao longo do tempo ou para comparar diferentes grupos de dados. A linha que une os pontos no gráfico poligonal ajuda a visualizar a tendência dos dados, mostrando se há um aumento, diminuição ou estabilidade nas informações apresentadas.
Um exemplo de gráfico poligonal seria um gráfico que representa a variação da temperatura ao longo de um ano. Cada ponto no gráfico seria a temperatura registrada em um determinado mês, e a linha que os conecta mostraria a variação da temperatura ao longo do tempo. Dessa forma, seria possível identificar padrões sazonais e tendências de aumento ou diminuição da temperatura.
Quais são as características e propriedades das funções polinomiais?
As funções polinomiais são funções matemáticas que podem ser expressas na forma de um polinômio, ou seja, uma soma de termos que contêm variáveis elevadas a expoentes inteiros não negativos. Essas funções são caracterizadas por algumas propriedades importantes que as distinguem de outras funções matemáticas.
Uma das principais características das funções polinomiais é que elas são contínuas em todos os números reais. Isso significa que não há “buracos” ou “quebras” no gráfico de uma função polinomial, tornando-a suave e sem interrupções. Além disso, as funções polinomiais são infinitamente diferenciáveis, o que significa que é possível calcular suas derivadas em qualquer ponto.
Outra propriedade das funções polinomiais é que elas podem ter um número finito de raízes, ou seja, valores de x que fazem a função igual a zero. O grau de um polinômio determina o número máximo de raízes que ele pode ter, de acordo com o Teorema Fundamental da Álgebra.
Um exemplo de função polinomial é a função quadrática, que pode ser expressa na forma f(x) = ax^2 + bx + c, onde a, b e c são constantes e a ≠ 0. O gráfico de uma função quadrática é uma parábola, uma curva suave e simétrica que pode abrir para cima ou para baixo, dependendo do valor de a.
Em resumo, as funções polinomiais são funções matemáticas contínuas, suaves e infinitamente diferenciáveis, que podem ter um número finito de raízes. Elas são expressas na forma de polinômios e apresentam propriedades distintas que as tornam importantes no estudo da matemática e em diversas aplicações práticas.
Qual a finalidade de um gráfico na representação visual de dados estatísticos?
Os gráficos são ferramentas essenciais na representação visual de dados estatísticos, pois permitem uma visualização mais clara e rápida das informações. A finalidade principal de um gráfico é facilitar a interpretação dos dados, tornando mais fácil identificar tendências, padrões e relações entre variáveis.
Um dos tipos de gráficos mais utilizados é o gráfico poligonal, que é uma representação gráfica de dados estatísticos por meio de linhas que ligam os pontos correspondentes às variáveis. Esse tipo de gráfico é útil para mostrar a evolução de uma variável ao longo do tempo ou comparar diferentes grupos de dados.
Um exemplo de gráfico poligonal pode ser visto na representação da evolução das vendas de uma empresa ao longo de um ano. Os meses do ano são representados no eixo horizontal e as vendas em milhares de reais no eixo vertical. Ligando os pontos correspondentes a cada mês, é possível visualizar de forma clara se houve um aumento, queda ou estabilidade nas vendas ao longo do ano.
Em resumo, os gráficos, como o gráfico poligonal, são importantes ferramentas na análise e interpretação de dados estatísticos, pois facilitam a compreensão das informações de forma visual e intuitiva.
O que é um gráfico poligonal? (com exemplos)
Um gráfico poligonal é um gráfico linear normalmente usado por estatísticas para comparar dados e representar a magnitude ou frequência de determinadas variáveis.
Em outras palavras, um gráfico poligonal é aquele que pode ser encontrado em um plano cartesiano, onde duas variáveis são relacionadas e os pontos marcados entre elas são unidos para formar uma linha contínua e irregular.
Um gráfico poligonal serve ao mesmo objetivo de um histograma, mas é particularmente útil para comparar grupos de dados. Além disso, é uma boa alternativa para mostrar distribuições de frequência cumulativas.
Nesse sentido, o termo frequência é entendido como o número de vezes que um evento ocorre dentro de uma amostra.
Todos os gráficos poligonais são estruturados inicialmente como histogramas. Dessa forma, um eixo X (horizontal) e um eixo Y (vertical) são marcados.
Além disso, variáveis com seus respectivos intervalos e frequências são escolhidas para medir os referidos intervalos. Geralmente, as variáveis são marcadas no plano de X e as frequências no de Y.
Uma vez que as variáveis e frequências foram estabelecidas nos eixos X e Y, os pontos que as relacionam dentro do plano são marcados.
Esses pontos são posteriormente unidos, formando uma linha contínua e irregular, conhecida como gráfico poligonal (Education, 2017).
Função de gráfico poligonal
A principal função de um gráfico poligonal é indicar as mudanças sofridas por um fenômeno dentro de um período de tempo definido ou em relação a outro fenômeno conhecido como frequência.
Dessa forma, é uma ferramenta útil para comparar o estado das variáveis ao longo do tempo ou em oposição a outros fatores (Lane, 2017).
Alguns exemplos comuns que podem ser evidenciados na vida cotidiana incluem a análise da variação de preços de determinados produtos ao longo dos anos, a mudança no peso corporal, o aumento do salário mínimo de um país e, em geral.
Em termos gerais, um gráfico poligonal é usado quando você deseja representar visualmente a variação de um fenômeno ao longo do tempo, a fim de estabelecer comparações quantitativas.
Este gráfico é derivado em muitos casos de um histograma, em que os pontos marcados no plano cartesiano correspondem aos que cobrem as barras do histograma.
Representação gráfica
Diferentemente do histograma, o gráfico poligonal não usa barras de diferentes alturas para marcar a alteração das variáveis dentro de um tempo definido.
O gráfico usa segmentos de linha que sobem ou descem dentro do plano cartesiano, dependendo do valor dado aos pontos que marcam a mudança no comportamento das variáveis no eixo X e no Y.
Graças a essa particularidade, o gráfico poligonal recebe seu nome, pois a figura resultante da união dos pontos com segmentos de linha no plano cartesiano é um polígono com segmentos retos consecutivos.
Uma característica importante que deve ser levada em consideração quando você deseja representar um gráfico poligonal é que tanto as variáveis no eixo X quanto as frequências no eixo Y devem ser marcadas com o título do que estão medindo.
Dessa forma, é possível a leitura das variáveis quantitativas contínuas incluídas no gráfico.
Por outro lado, para fazer um gráfico poligonal, dois intervalos nas extremidades devem ser adicionados, cada um com o mesmo tamanho e uma frequência equivalente a zero.
Dessa forma, o limite superior e inferior da variável analisada é obtido e cada uma é dividida por dois, para determinar o local onde a linha do gráfico poligonal deve começar e terminar (Xiwhanoki, 2012).
Finalmente, a localização dos pontos no gráfico dependerá dos dados anteriormente disponíveis para a variável e a frequência.
Esses dados devem ser organizados em pares cuja localização no plano cartesiano será representada por um ponto. Para formar o gráfico poligonal, os pontos devem ser unidos da esquerda para a direita.
Exemplos de gráficos poligonais
Exemplo 1
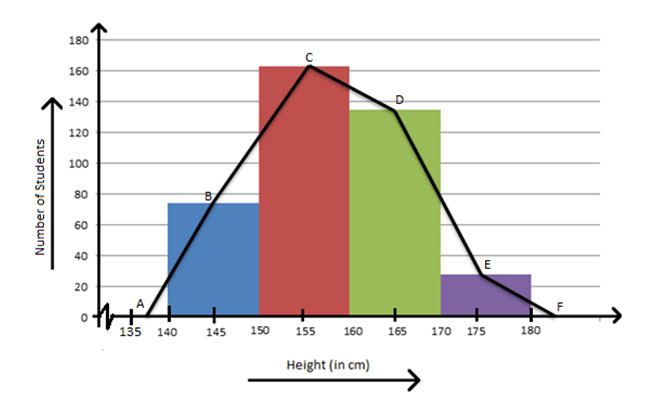
Em um grupo de 400 alunos, sua altura é expressa na tabela a seguir:
O gráfico poligonal desta tabela seria o seguinte:
A altura dos alunos é representada no eixo X ou eixo horizontal em uma escala definida em cm, como indica o título, cujo valor aumenta a cada cinco unidades.
Por outro lado, o número de alunos é representado no eixo Y ou eixo vertical em uma escala que aumenta seu valor a cada 20 unidades.
As barras retangulares neste gráfico correspondem às de um histograma. No entanto, dentro do gráfico poligonal, essas barras são usadas para representar a largura do intervalo de classe coberto por cada variável, e sua altura marca a frequência correspondente a cada um desses intervalos (ByJu’s, 2016).
Exemplo 2
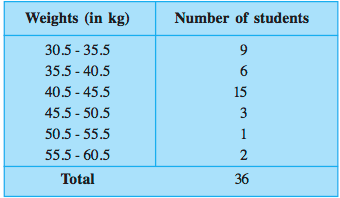
Em um grupo de 36 alunos, será feita uma análise do peso de acordo com as informações coletadas na tabela a seguir:
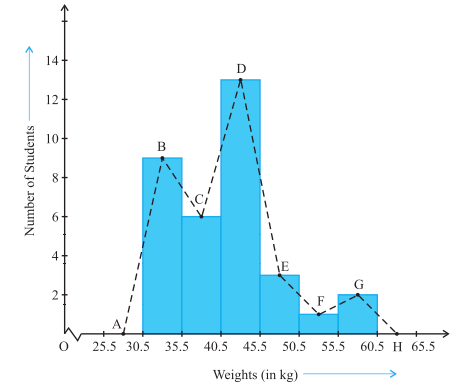
O gráfico poligonal desta tabela seria o seguinte:
Dentro do eixo X ou eixo horizontal, os pesos dos alunos em quilogramas são representados. O intervalo da aula aumenta a cada 5 kg.
No entanto, entre o zero e o primeiro ponto do intervalo, uma irregularidade no plano foi marcada para indicar que esse primeiro espaço representa um valor maior que 5 kg.
No eixo vertical, a frequência é expressa, ou seja, o número de alunos, avançando em uma escala cujo número aumenta a cada duas unidades.
Essa escala é estabelecida levando em consideração os valores dados na tabela onde as informações iniciais foram coletadas.
Neste exemplo, como no anterior, os retângulos são usados para marcar os intervalos de classe mostrados na tabela.
No entanto, no gráfico poligonal, as informações relevantes são obtidas a partir da linha resultante da junção dos pontos resultantes do par de dados relacionados na tabela (Net, 2017).
Referências
- ByJu’s. (11 de agosto de 2016). ByJu’s . Obtido dos polígonos de frequência: byjus.com
- Educação, MS (2017). Álgebra, Geometria e Estatística do Ensino Médio / Médio (AGS). Em MH Education, Álgebra do Ensino Médio / Médio, Geometria e Estatística (AGS) (p. 48). McGraw Hill
- Lane, DM (2017). Rice University . Obtido em Frequency Polygons: onlinestatbook.com.
- Net, K. (2017). Kwiz Net . Obtido em Álgebra, Geometria e Estatística do Ensino Médio / Médio (AGS): kwiznet.com.
- (1 de setembro de 2012). Clube de Ensaios . Obtido do que é um gráfico poligonal?: Clubensayos.com.