Ângulos alternativos internos são pares de ângulos que estão no lado interno das retas paralelas cortadas por uma transversal. Eles possuem a mesma medida e são formados por lados opostos da transversal. Esses ângulos são muito importantes na geometria, pois ajudam a determinar a congruência de figuras geométricas e a resolver problemas de medidas de ângulos.
A melhor forma de compreender e praticar o conceito de ângulos alternativos internos é por meio de exercícios. A resolução de problemas envolvendo esses ângulos ajuda a reforçar o entendimento teórico e a desenvolver habilidades de raciocínio geométrico. Vamos agora explorar alguns exercícios para praticar esse conceito.
Definição de ângulo alterno interno em um par de retas transversais.
Os ângulos alternos internos são formados quando duas retas transversais cortam duas retas paralelas. Nesse caso, os ângulos alternos internos estão localizados em lados opostos da transversal e do mesmo lado das retas paralelas.
Para identificar os ângulos alternos internos em um par de retas transversais, basta observar os ângulos que estão do mesmo lado da transversal e em lados opostos das retas paralelas. Esses ângulos são congruentes, ou seja, possuem a mesma medida.
Portanto, a definição de ângulo alterno interno é fundamental para resolver problemas envolvendo paralelas cortadas por uma transversal. Ao identificar os ângulos alternos internos, é possível utilizar suas propriedades para encontrar medidas desconhecidas e resolver questões matemáticas.
Vamos praticar com um exercício: se os ângulos alternos internos em um par de retas transversais medem 70 graus e x graus, qual é a medida do ângulo x?
Para resolver esse exercício, basta lembrar que os ângulos alternos internos são congruentes. Portanto, se um ângulo mede 70 graus, o outro ângulo também deve medir 70 graus. Assim, a medida do ângulo x é 70 graus.
Entenda a definição e a importância dos ângulos internos em figuras geométricas.
Os ângulos internos são fundamentais para a compreensão e análise de figuras geométricas. Eles são formados pela intersecção de duas retas ou segmentos de retas em um determinado ponto, conhecido como vértice. Esses ângulos podem ser classificados de acordo com a sua medida em agudo, reto, obtuso, raso e completo.
A importância dos ângulos internos está relacionada à sua capacidade de determinar a forma e as propriedades de diferentes figuras geométricas. Eles são essenciais para o cálculo de áreas, perímetros e outras grandezas relacionadas às figuras. Além disso, os ângulos internos são utilizados em diversas áreas da Matemática e da Física, sendo aplicados em problemas práticos e teóricos.
Um tipo específico de ângulo interno são os ângulos alternativos internos. Esses ângulos são formados por duas retas paralelas cortadas por uma transversal. Os ângulos alternativos internos são congruentes, ou seja, têm a mesma medida. Isso significa que, se um ângulo alternativo interno mede x graus, o seu correspondente também terá x graus.
Para exemplificar, considere duas retas paralelas cortadas por uma transversal. Se um ângulo alternativo interno é de 60 graus, então o ângulo correspondente também será de 60 graus. Essa propriedade dos ângulos alternativos internos é muito útil em problemas de geometria e trigonometria, facilitando o cálculo de medidas e a resolução de questões.
Em resumo, os ângulos internos desempenham um papel fundamental na geometria e em outras áreas da Matemática. Os ângulos alternativos internos, em particular, possuem uma propriedade importante que facilita a resolução de problemas envolvendo retas paralelas e transversais. É essencial compreender e dominar o conceito de ângulos internos para explorar as propriedades das figuras geométricas e resolver questões de forma eficiente.
Como calcular os ângulos internos alternos de forma simples e eficiente.
Os ângulos alternos internos são formados quando duas retas paralelas são cortadas por uma transversal. Eles são chamados de alternos internos porque estão localizados no interior das duas retas paralelas, em posições opostas. Para calcular esses ângulos, basta lembrar que eles são congruentes, ou seja, têm a mesma medida.
Para encontrar os ângulos alternos internos, basta seguir dois passos simples. Primeiro, identifique os ângulos correspondentes em relação à transversal. Em seguida, lembre-se de que os ângulos alternos internos são congruentes, ou seja, têm a mesma medida.
Vamos a um exemplo prático: Se tivermos duas retas paralelas cortadas por uma transversal, e um dos ângulos formados pela transversal e uma das retas paralelas medir 60 graus, então o ângulo correspondente a ele do outro lado da transversal também medirá 60 graus. Esses são os ângulos alternos internos.
Portanto, para calcular os ângulos internos alternos de forma simples e eficiente, basta lembrar que eles são congruentes e têm a mesma medida em casos de retas paralelas cortadas por uma transversal.
Quais são os pares de ângulos internos alternos em uma figura geométrica?
Os ângulos alternos internos são pares de ângulos que ocupam posições opostas em relação a uma linha transversal em uma figura geométrica. Em outras palavras, são ângulos que estão do mesmo lado da linha transversal, mas em lados opostos da linha que corta duas linhas paralelas.
Quando duas linhas paralelas são cortadas por uma transversal, os pares de ângulos internos alternos são formados por ângulos que não estão do mesmo lado da transversal, mas estão em lados opostos da linha. Por exemplo, se temos duas linhas paralelas cortadas por uma transversal, um par de ângulos internos alternos seria o ângulo 1 e o ângulo 2, e outro par seria o ângulo 3 e o ângulo 4.
Para identificar os pares de ângulos internos alternos em uma figura geométrica, basta procurar por ângulos que estão do mesmo lado da transversal, mas em lados opostos da linha que corta as linhas paralelas.
Exercícios:
1. Na figura abaixo, identifique os pares de ângulos internos alternos:
Resposta: Os pares de ângulos internos alternos são: ângulo 1 e ângulo 5, ângulo 2 e ângulo 6, ângulo 3 e ângulo 7, ângulo 4 e ângulo 8.
2. Determine os pares de ângulos internos alternos na figura a seguir:
Resposta: Os pares de ângulos internos alternos são: ângulo A e ângulo E, ângulo B e ângulo F, ângulo C e ângulo G, ângulo D e ângulo H.
O que são ângulos alternativos internos? (Com exercícios)
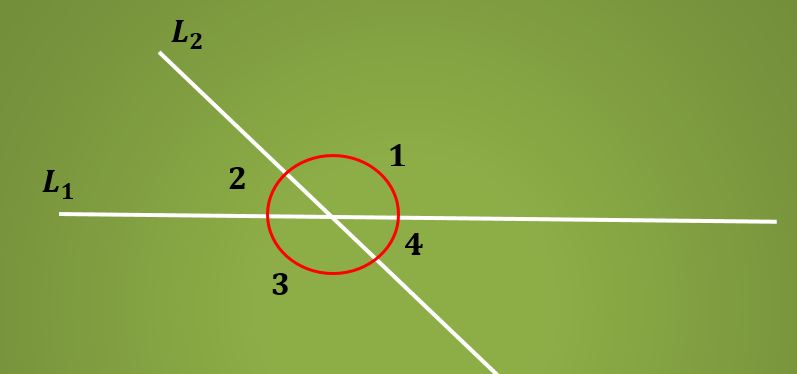
As alternativas interiores ângulos são os ângulos formados pela intersecção de duas linhas paralelas e uma linha transversal. Quando uma linha L1 é cortada por uma linha transversal L2, 4 ângulos são formados.
Os dois pares de ângulos que permanecem no mesmo lado da linha L1 são chamados ângulos suplementares, uma vez que sua soma é igual a 180 °.
Na imagem anterior, os ângulos 1 e 2 são complementares, assim como os ângulos 3 e 4.
Para poder falar sobre ângulos alternativos internos, é necessário ter duas linhas paralelas e uma linha transversal; como visto anteriormente, oito ângulos serão formados.
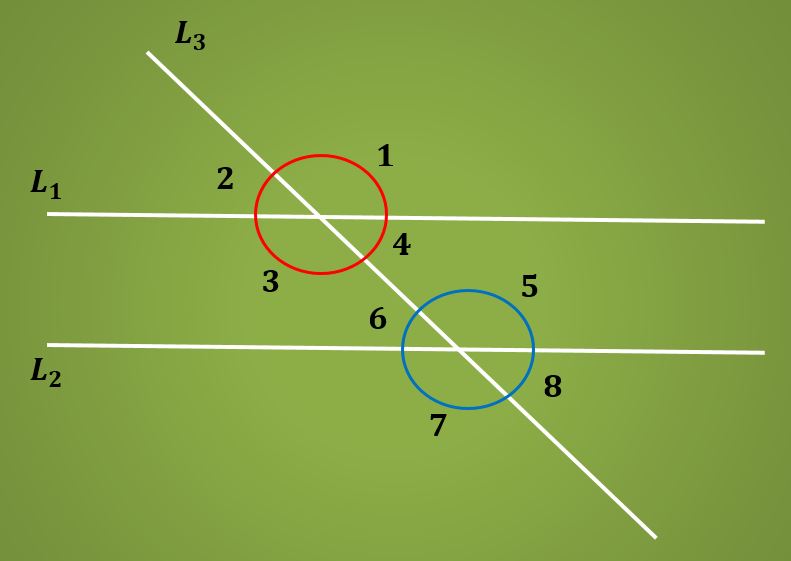
Quando existem duas linhas paralelas L1 e L2 cortadas por uma linha transversal, oito ângulos são formados, conforme ilustrado na imagem a seguir.
Na imagem anterior, os pares de ângulos 1 e 2, 3 e 4, 5 e 6, 7 e 8 são ângulos suplementares.
Agora, os ângulos alternos internos são aqueles entre as duas linhas paralelas L1 e L2, mas estão localizados em lados opostos da linha transversal L2.
Ou seja, os ângulos 3 e 5 são alternativos internos. Da mesma forma, os ângulos 4 e 6 são ângulos internos alternativos.
Ângulos opostos pelo vértice
Para conhecer a utilidade dos ângulos alternativos internos, é necessário primeiro saber que, se dois ângulos são opostos pelo vértice, esses dois ângulos medem o mesmo.
Por exemplo, os ângulos 1 e 3 medem o mesmo sendo opostos pelo vértice. Sob o mesmo raciocínio, pode-se concluir que os ângulos 2 e 4, 5 e 7, 6 e 8 medem o mesmo.
Ângulos formados entre um secante e dois paralelos
Quando existem duas linhas paralelas cortadas por uma linha secante ou transversal, como na figura anterior, é verdade que os ângulos 1 e 5, 2 e 6, 3 e 7, 4 e 8 medem o mesmo.
Ângulos alternativos internos
Usando a definição de ângulos definida pelo vértice e a propriedade dos ângulos formados entre uma secante e duas linhas paralelas, pode-se concluir que os ângulos alternos internos têm a mesma medida.
Exercícios
Primeiro exercício
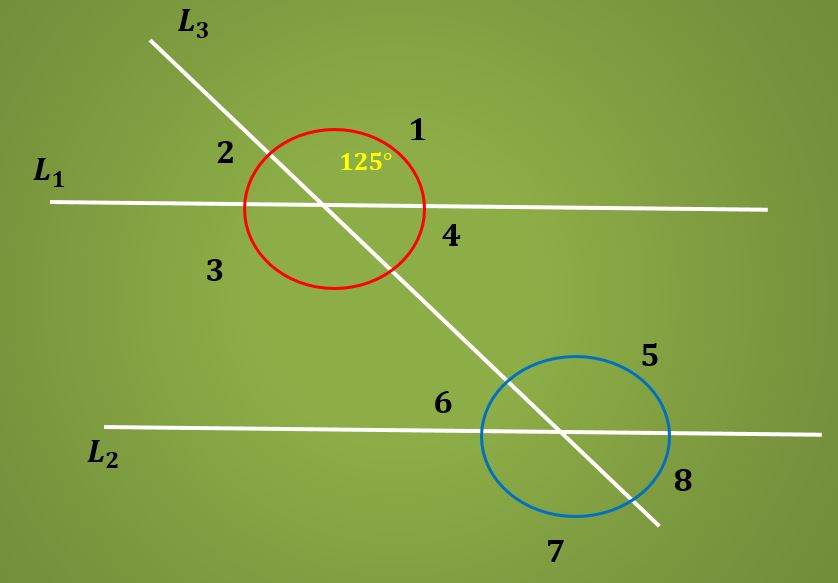
Calcule a medida do ângulo 6 da imagem a seguir, sabendo que o ângulo 1 mede 125º.
Solução
Como os ângulos 1 e 5 são opostos pelo vértice, o ângulo 3 é medido 125º. Agora, como os ângulos 3 e 5 são alternativos internos, o ângulo 5 também é medido 125 °.
Finalmente, como os ângulos 5 e 6 são complementares, a medida do ângulo 6 é igual a 180º – 125º = 55º.
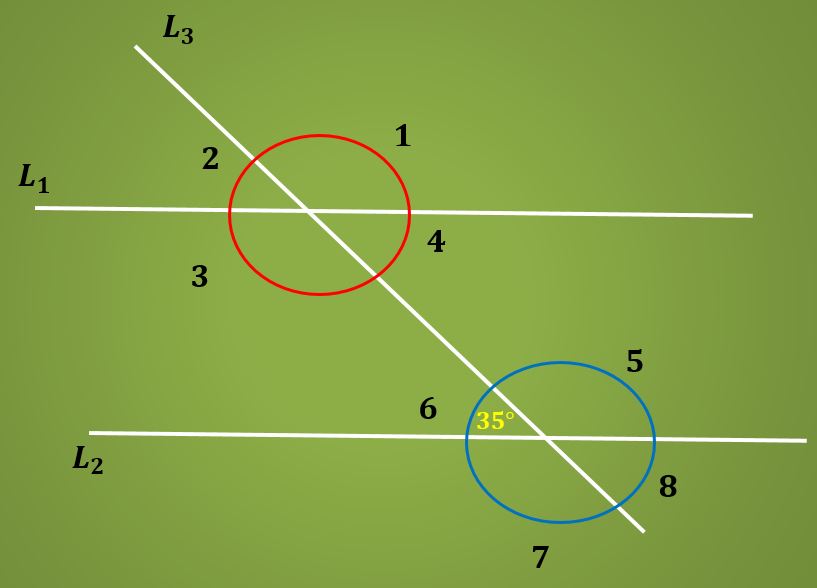
2º exercício
Calcule a medida do ângulo 3 sabendo que o ângulo 6 mede 35º.
Solução
Sabe-se que o ângulo 6 mede 35 ° e também se sabe que os ângulos 6 e 4 são alternativos internos, portanto, medem o mesmo. Ou seja, o ângulo 4 mede 35º.
Por outro lado, usando o fato de que os ângulos 4 e 3 são complementares, a medida do ângulo 3 é igual a 180º – 35º = 145º.
Observação
É necessário que as linhas sejam paralelas para que possam atender às propriedades correspondentes.
Os exercícios podem ser resolvidos mais rapidamente, mas neste artigo queríamos usar a propriedade de ângulos alternativos internos.
Referências
- Bourke (2007). Um ângulo na pasta de trabalho de matemática em geometria. NewPath Learning
- C., E. Á. (2003). Elementos de geometria: com vários exercícios e geometria da bússola. Universidade de Medellín.
- Clemens, SR, O’Daffer, PG, & Cooney, TJ (1998). Geometria Pearson Education.
- Lang, S. & Murrow, G. (1988). Geometria: um curso de ensino médio. Springer Science & Business Media.
- Lira, A., Jaime, P., Chavez, M., Gallegos, M. e Rodríguez, C. (2006). Geometria e Trigonometria. Edições de limite.
- Moyano, AR, Saro, AR e Ruiz, RM (2007). Álgebra e Geometria Quadrática. Netbiblo
- Palmer, CI, & Bibb, SF (1979). Matemática prática: aritmética, álgebra, geometria, trigonometria e regra de cálculo. Reverte
- Sullivan, M. (1997). Trigonometria e geometria analítica. Pearson Education.
- Wingard-Nelson, R. (2012). Geometria Enslow Publishers, Inc. Empresas