O círculo e a circunferência são elementos fundamentais da geometria e frequentemente confundidos entre si. Embora ambos se refiram a formas circulares, existem diferenças significativas entre eles. Neste artigo, discutiremos cinco diferenças essenciais entre círculo e circunferência, a fim de esclarecer suas distinções e facilitar a compreensão desses conceitos geométricos.
Diferenças entre círculo e circunferência explicadas de forma simplificada.
Círculo e Circunferência são conceitos matemáticos que muitas vezes são confundidos, mas na verdade têm significados diferentes. Aqui estão 5 diferenças entre eles:
1. Definição: Um círculo é a região plana delimitada por uma linha curva, chamada circunferência. A circunferência, por sua vez, é a linha curva que forma o contorno de um círculo.
2. Elementos: O círculo é formado por todos os pontos no plano que estão a uma distância fixa de um ponto central, chamado de centro. Já a circunferência é apenas a linha que delimita o círculo.
3. Comprimento: O comprimento da circunferência é calculado utilizando a fórmula 2πr, onde r é o raio da circunferência. Já o perímetro do círculo corresponde ao comprimento da circunferência.
4. Área: A área do círculo é calculada utilizando a fórmula πr², onde r é o raio do círculo. Já a circunferência não possui área, pois é apenas uma linha.
5. Representação: Enquanto o círculo é representado por uma região preenchida no plano, a circunferência é representada por uma linha curva.
Portanto, é importante entender a diferença entre círculo e circunferência para não confundir os dois conceitos em problemas matemáticos.
Quais são os componentes essenciais que compõem uma circunferência?
Uma circunferência é formada por cinco componentes essenciais: o centro, o raio, o diâmetro, a corda e o arco. O centro é o ponto dentro da circunferência de onde partem todas as medidas. O raio é a distância do centro até qualquer ponto da circunferência. O diâmetro é a medida que atravessa o centro e é o dobro do raio. A corda é um segmento de reta que une dois pontos da circunferência. E o arco é a parte da circunferência compreendida entre dois pontos.
5 Diferenças entre Círculo e Circunferência
1. Definição: Um círculo é a região plana delimitada por uma circunferência, enquanto a circunferência é apenas a linha curva que forma a borda do círculo.
2. Elementos: O círculo possui apenas uma medida de raio, enquanto a circunferência possui centro, raio, diâmetro, corda e arco.
3. Área e Perímetro: A área de um círculo é calculada usando a fórmula π*r², enquanto o perímetro de uma circunferência é calculado usando a fórmula 2*π*r.
4. Aplicações: Os círculos são frequentemente usados em geometria para representar formas planas, enquanto as circunferências são usadas em problemas de trigonometria e cálculo.
5. Representação: Um círculo pode ser desenhado como uma forma fechada, enquanto uma circunferência é representada apenas por uma linha curva.
Exemplos de círculos e suas aplicações práticas na geometria e matemática.
Um dos conceitos fundamentais na geometria e matemática é o círculo. O círculo é uma figura geométrica plana formada por todos os pontos que estão a uma mesma distância de um ponto fixo chamado centro. A circunferência, por outro lado, é a linha curva que delimita o círculo. Vamos então discutir cinco diferenças entre círculo e circunferência.
1. Definição
Enquanto o círculo é a região plana contida dentro da circunferência, a circunferência é apenas a linha que forma o contorno do círculo.
2. Elementos
Um círculo possui raio, diâmetro, centro e área, enquanto a circunferência possui apenas comprimento.
3. Representação
Na representação gráfica, um círculo é uma figura preenchida, enquanto uma circunferência é apenas uma linha curva.
4. Aplicações práticas
Os círculos são amplamente utilizados em engenharia civil para o projeto de estruturas circulares, como pontes e túneis. Já as circunferências são usadas em navegação marítima para determinar a posição de um navio em relação a um ponto de referência.
5. Fórmulas
Para calcular a área de um círculo, utiliza-se a fórmula A = πr², onde r é o raio. Já o comprimento de uma circunferência é dado por C = 2πr, onde r é o raio.
Em resumo, o círculo e a circunferência são conceitos interligados, mas com diferenças claras em suas definições, elementos, representações, aplicações práticas e fórmulas matemáticas.
Principais características de uma circunferência: o que você precisa saber sobre esse formato geométrico.
Uma circunferência é uma linha curva fechada, onde todos os pontos estão à mesma distância de um ponto central chamado centro. É importante entender as principais características desse formato geométrico para aplicá-lo corretamente em problemas matemáticos e construções. Aqui estão 5 diferenças entre círculo e circunferência:
1. Definição: Um círculo é a região plana delimitada por uma circunferência, ou seja, é a área interna da circunferência. Já a circunferência é apenas a linha curva que define o contorno do círculo.
2. Elementos: Um círculo possui raio, diâmetro, circunferência e área. Já a circunferência é definida apenas pelo seu raio e centro.
3. Medidas: O raio de um círculo é a distância do centro à circunferência, enquanto o diâmetro é o dobro do raio. Já a circunferência é encontrada multiplicando o diâmetro por π (pi).
4. Aplicações: Os círculos são comumente usados em geometria, engenharia, arquitetura e diversas outras áreas. Já as circunferências são essenciais para encontrar o perímetro de figuras circulares e calcular distâncias entre pontos em um plano.
5. Representação: Enquanto um círculo pode ser desenhado como uma forma preenchida em um plano, a circunferência é representada por uma linha curva sem largura.
5 Diferenças entre Círculo e Circunferência
Um círculo e uma circunferência são dois conceitos geométricos muito semelhantes, porém mencionam dois objetos diferentes. Em muitas ocasiões, é cometido o erro de chamar um círculo e vice-versa.Neste artigo, algumas diferenças entre esses dois conceitos serão mencionadas.
Esses conceitos são diferentes em vários aspectos, tais como: suas definições, as equações cartesianas que os representam, a região do plano cartesiano que ocupam e as figuras tridimensionais que formam.
Para observar as diferenças no desenho de um círculo e um círculo, é conveniente usar cores ao desenhá-las.
Principais diferenças entre um círculo e um círculo
Definições
Circunferência : um círculo é uma curva fechada, de modo que todos os pontos da curva estão a uma distância fixa “r”, chamada raio, de um ponto fixo “C”, chamado centro do círculo.
Círculo : é a região do plano que é delimitada por um círculo, ou seja, são todos os pontos que estão dentro de um círculo.
Também se pode dizer que um círculo é todos os pontos que estão a uma distância menor ou igual a “r” do ponto “C”.
Aqui você pode notar a primeira diferença entre esses conceitos, já que um círculo é apenas uma curva fechada, enquanto um círculo são as regiões do plano delimitadas por um círculo.
Equações cartesianas
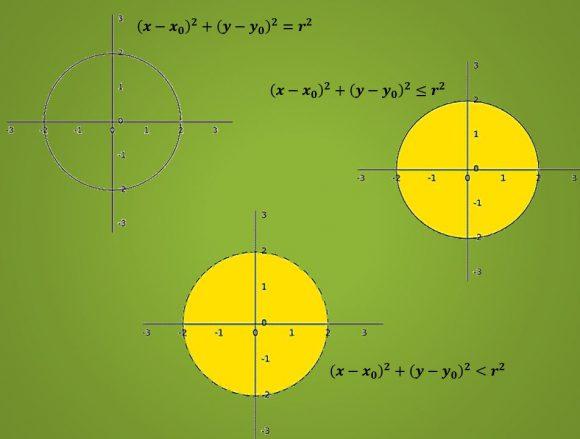
A equação cartesiana que representa um círculo é (x-x0) ² + (y-y0) ² = r², onde “x0” e “y0” são as coordenadas cartesianas do centro do círculo e “r” é o raio.
Por outro lado, a equação cartesiana de um círculo é (x-x0) ² + (y-y0) ² ≤ r² ou (x-x0) ² + (y-y0) ² <r².
A diferença entre as equações é que na circunferência é sempre uma igualdade, enquanto no círculo é uma desigualdade.
Uma conseqüência disso é que o centro de um círculo não pertence ao círculo, enquanto o centro de um círculo sempre pertence ao círculo.
Gráficos no plano cartesiano
Devido às definições mencionadas no item 1, você pode ver que os gráficos de um círculo e um círculo são:
Nas imagens você pode ver a diferença mencionada no item 1. Além disso, é feita uma distinção entre as duas possíveis equações cartesianas de um círculo. Quando a desigualdade é estrita, a aresta do círculo não é incluída no gráfico.
Dimensões
Outra diferença que pode ser notada é com relação às dimensões desses dois objetos.
Como um círculo é apenas uma curva, esta é uma figura unidimensional, portanto, é apenas comprimento. Um círculo, pelo contrário, é uma figura bidimensional, portanto, possui comprimento e largura, portanto possui uma área associada.
O comprimento de um círculo de raio «r» é igual a 2π * r, e a área de um círculo de raio «r» é π * r².
Figuras tridimensionais que geram
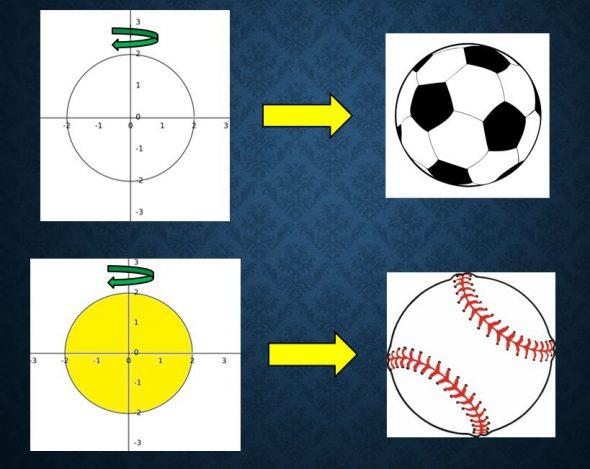
Se o gráfico de um círculo for considerado e girado em torno de uma linha que passa pelo centro, será obtido um objeto tridimensional que é uma esfera.
É claro que essa esfera é oca, ou seja, é apenas a borda. Um exemplo de esfera é uma bola de futebol porque só existe ar dentro dela.
Por outro lado, se o mesmo procedimento for realizado com um círculo, uma esfera será obtida, mas será preenchida, ou seja, a esfera não será oca.
Um exemplo dessa esfera cheia pode ser uma bola de beisebol.
Portanto, os objetos tridimensionais gerados dependem de um círculo ou círculo ser usado.
Referências
- Basto, JR (2014). Matemática 3: Geometria analítica básica. Grupo Editorial Patria.
- Billstein, R., Libeskind, S., & Lott, JW (2013). Matemática: uma abordagem de resolução de problemas para professores do ensino fundamental. Editores López Mateos.
- Bult, B. & Hobbs, D. (2001). Léxico da matemática (ed. Ilustrado). (FP Chain, Trad.) Edições AKAL.
- Callejo, I., Aguilera, M., Martínez, L., & Aldea, CC (1986). Matemática Geometria Reforma do ciclo superior do Ministério da Educação da EGB .
- Schneider, W. & Sappert, D. (1990). Manual prático de desenho técnico: introdução aos fundamentos do desenho técnico industrial. Reverte
- Thomas, GB e Weir, MD (2006). Cálculo: várias variáveis. Pearson Education.