Os números racionais são uma parte fundamental do conjunto dos números reais, representando valores que podem ser expressos na forma de fração, ou seja, como uma razão entre dois números inteiros. Neste contexto, os números racionais apresentam diversas propriedades matemáticas que os tornam úteis em uma variedade de situações, tais como adição, subtração, multiplicação e divisão. Neste artigo, exploraremos algumas das propriedades dos números racionais, forneceremos exemplos de sua aplicação e discutiremos as operações básicas envolvendo esses números.
Características dos números racionais: conheça as propriedades que os definem.
Números racionais são números que podem ser expressos na forma de fração, ou seja, são representados por um numerador e um denominador. As principais características dos números racionais são suas propriedades matemáticas que os definem e os diferenciam de outros tipos de números.
Uma das propriedades dos números racionais é que eles podem ser escritos na forma a/b, onde “a” e “b” são números inteiros e b não é igual a zero. Isso significa que os números racionais podem ser representados por uma fração que pode ser simplificada.
Além disso, os números racionais são números que podem ser finitos ou infinitos, tanto na parte inteira quanto na parte decimal. Isso significa que tanto números inteiros como números periódicos podem ser considerados racionais.
Outra característica importante dos números racionais é que eles são fechados em relação às operações matemáticas de adição, subtração, multiplicação e divisão. Isso significa que ao realizar operações com números racionais, o resultado também será um número racional.
Para exemplificar, podemos citar números como 1/2, 3/4, -5/7, entre outros, como exemplos de números racionais. Esses números podem ser somados, subtraídos, multiplicados e divididos entre si, mantendo sempre sua característica de número racional.
Essas propriedades definem os números racionais e os tornam fundamentais no estudo da matemática.
Exemplos de operações com números racionais: adição, subtração, multiplicação e divisão.
Números racionais são aqueles que podem ser expressos na forma de fração, onde o numerador e o denominador são inteiros e o denominador é diferente de zero. As operações com números racionais seguem as mesmas regras das operações com números inteiros, porém é importante lembrar das propriedades específicas dos racionais.
Para realizar a adição de números racionais, basta somar os numeradores mantendo o denominador comum. Por exemplo, 1/2 + 3/4 = (1*4 + 3*2)/(2*4) = 10/8 = 5/4.
Na subtração de números racionais, subtraímos os numeradores mantendo o denominador comum. Um exemplo seria 5/3 – 2/5 = (5*5 – 2*3)/(3*5) = 23/15.
Para multiplicar números racionais, multiplicamos os numeradores entre si e os denominadores entre si. Por exemplo, 2/3 * 4/5 = (2*4)/(3*5) = 8/15.
Por fim, na divisão de números racionais, multiplicamos o primeiro pelo inverso do segundo. Por exemplo, 3/4 ÷ 1/2 = 3/4 * 2/1 = 6/4 = 3/2.
É importante sempre simplificar as frações resultantes das operações, quando possível, para obter os números racionais de forma mais simplificada e clara.
Exemplos de números racionais e sua definição.
Números racionais são aqueles que podem ser representados na forma de fração, ou seja, são números que podem ser escritos na forma a/b, onde a e b são inteiros e b é diferente de zero. Em outras palavras, um número racional é qualquer número que pode ser expresso como a razão de dois inteiros.
Alguns exemplos de números racionais são 1/2, -3/4, 5/1, 0, -7, 2.5, -0.333… e assim por diante. Note que os números inteiros também são considerados números racionais, pois podem ser escritos na forma de fração.
Os números racionais possuem algumas propriedades interessantes. Por exemplo, a soma, subtração, multiplicação e divisão de números racionais resulta sempre em outro número racional. Além disso, o conjunto dos números racionais é fechado em relação às operações de adição e multiplicação, ou seja, a soma e o produto de dois números racionais é sempre outro número racional.
Eles possuem propriedades específicas que os diferenciam de outros tipos de números, como os irracionais.
Entendendo as principais características das operações matemáticas.
Números racionais são números que podem ser expressos na forma de uma fração, onde o numerador e o denominador são inteiros e o denominador é diferente de zero. Eles possuem algumas propriedades importantes que nos ajudam a entender melhor como as operações matemáticas funcionam.
Uma das principais propriedades dos números racionais é a fechamento em relação às operações de adição e multiplicação. Isso significa que ao somar ou multiplicar dois números racionais, o resultado também será um número racional. Por exemplo, se somarmos 1/2 com 2/3, obteremos 7/6, que é um número racional.
Outra propriedade importante dos números racionais é a existência do elemento neutro em relação à adição e multiplicação. O elemento neutro da adição é o zero, pois qualquer número racional somado a zero resulta no próprio número racional. Já o elemento neutro da multiplicação é o um, pois qualquer número racional multiplicado por um resulta no próprio número racional.
Além disso, os números racionais também possuem a propriedade comutativa e associativa em relação à adição e multiplicação. Isso significa que a ordem dos números não altera o resultado da operação, e podemos agrupar os números de diferentes formas sem alterar o resultado final.
Por fim, as operações de subtração e divisão de números racionais também seguem regras específicas, envolvendo o uso do inverso aditivo e do inverso multiplicativo. Por exemplo, para subtrair 3/4 de 1/2, devemos encontrar o inverso aditivo de 3/4 e então realizar a adição.
Números racionais: propriedades, exemplos e operações

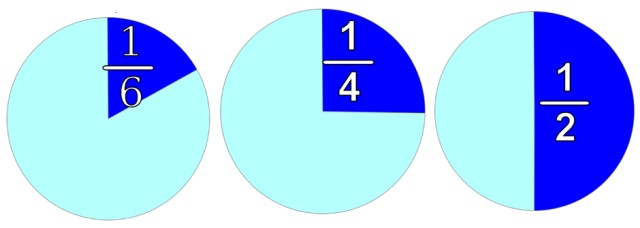
Os números racionais são todos os números que podem ser obtidos como a divisão de dois números inteiros. Exemplos de números racionais são: 3/4, 8/5, -16/3 e os que aparecem na figura a seguir. Em um número racional, o quociente é indicado, sendo possível fazê-lo posteriormente, se necessário.
A figura mostra qualquer objeto redondo por conveniência. Se queremos dividi-lo em 2 partes iguais, como à direita, temos duas metades e cada uma vale 1/2.
Ao dividi-lo em 4 partes iguais, obteremos 4 peças e cada uma vale 1/4, como na imagem ao centro. E se tiver que ser dividido em 6 partes iguais, cada parte valerá 1/6, o que vemos na imagem à esquerda.
Obviamente, também podemos dividi-lo em duas partes desiguais, por exemplo, podemos manter 3/4 partes e economizar 1/4 parte. Outras divisões também são possíveis, como 4/6 partes e 2/6 partes. O importante é que a soma de todas as partes seja 1.
Dessa maneira, é evidente que com números racionais você pode dividir, contar e distribuir coisas como comida, dinheiro, terra e todos os tipos de objetos em frações. E assim o número de operações que podem ser feitas com os números é expandido.
Os números racionais também podem ser expressos na forma decimal, como pode ser visto nos seguintes exemplos:
1/2 = 0,5
1/3 = 0,3333 …
3/4 = 0,75
1/7 = 0,142857142857142857 ………
Posteriormente, indicamos como ir de um formulário para outro com exemplos.
Propriedades de números racionais
Os números racionais, cujo conjunto iremos denotar com a letra Q, têm as seguintes propriedades:
-Q inclui números naturais N e números inteiros Z.
Tendo em conta que qualquer número a pode ser expresso como quociente entre si e 1, é fácil ver que entre os números racionais também existem naturais e inteiros.
Assim, o número natural 3 pode ser escrito como uma fração e também -5:
3 = 3/1
-5 = -5/1 = 5 / -1 = – (5/1)
Dessa maneira, Q é um conjunto numérico que engloba um número maior de números, algo muito necessário, pois os números “redondos” não são suficientes para descrever todas as operações possíveis a serem realizadas.
– Números racionais podem ser adicionados, subtraídos, multiplicados e divididos, resultando em um número racional: 1/2 + 1/5 = 7/10; 1/2 – 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.
– Entre cada par de números racionais, você sempre pode encontrar outro número racional. De fato, entre dois números racionais, existem números racionais infinitos.
Por exemplo, entre os números racionais 1/4 e 1/2 estão os números racionais 3/10, 7/20, 2/5 (e muitos mais), que podem ser verificados expressando-os como decimais.
– Qualquer número racional pode ser expresso como: i) um número inteiro ou ii) um decimal limitado (estrito) ou periódico: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,16666666 ……
-O mesmo número pode ser representado por frações equivalentes infinitas e todas elas pertencem a Q. Vamos ver este grupo:
Todos representam o decimal 0,428571 …
-De todas as frações equivalentes que representam o mesmo número, a fração irredutível, a mais simples de todas, é o representante canônico desse número. O representante canônico do exemplo anterior é 3/7.
Exemplos de números racionais
– Frações próprias, aquelas em que o numerador é menor que o denominador:
-Frações impróprias, cujo numerador é maior que o denominador:
-Números naturais e números inteiros:
-Frações equivalentes:
Representação decimal de um número racional
Quando o numerador é dividido pelo denominador, a forma decimal do número racional é encontrada. Por exemplo:
2/5 = 0,4
3/8 = 0,375
1/9 = 0,11111 …
11/6 = 0,545454…
Nos dois primeiros exemplos, o número de casas decimais é limitado. Isso significa que quando a divisão é finalmente feita, um restante 0 é obtido.
Por outro lado, nos dois seguintes, o número de casas decimais é infinito e, portanto, as reticências são colocadas. No último caso, há um padrão em decimais. No caso da fração 1/9, o número 1 é repetido indefinidamente, enquanto em 6/11 é 54.
Quando isso acontece, o decimal é considerado periódico e é denotado por um sotaque circunflexo como este:
Transformar um decimal em uma fração
Se for um número decimal limitado, a vírgula é simplesmente removida e o denominador se torna a unidade seguida por tantos zeros quantos houver números no número decimal. Por exemplo, para transformar o decimal 1,26 em uma fração, ele é escrito assim:
1,26 = 126/100
Em seguida, a fração resultante é simplificada ao máximo:
126/100 = 63/50
Se o decimal for ilimitado, o período será identificado primeiro. Em seguida, siga estas etapas para encontrar a fração resultante:
-O numerador é a subtração entre o número (sem vírgula ou acento circunflexo) e a parte que não possui o acento circunflexo.
-O denominador é um número inteiro com 9 quantos números sob o circunflexo e 0 como existem dígitos na parte decimal que não estão abaixo do circunflexo.
Vamos seguir este procedimento para transformar o número decimal 0,428428428 … em uma fração.
-Primeiro, o período é identificado, que é a sequência que se repete: 428.
-Em seguida, a operação é feita para subtrair o número sem vírgula ou acento: 0428 da parte que não possui um circunflexo, que é 0. Isso deixa 428 – 0 = 428.
-O denominador é construído, sabendo que existem 3 algarismos abaixo do circunflexo e todos eles estão abaixo do circunflexo. Portanto, o denominador é 999.
-Finalmente, a fração é formada e simplificada, se possível:
0,428 = 428/999
Não é possível simplificar ainda mais.
Operações com números racionais
– Adição e subtração
Frações com o mesmo denominador
Quando as frações têm o mesmo denominador, é muito fácil adicioná-las e / ou subtraí-las, porque os numeradores são simplesmente adicionados algebricamente, deixando a soma dos adendos como o denominador do resultado. Finalmente, se possível, é simplificado.
Exemplo
Execute a seguinte adição algébrica e simplifique o resultado:
A fração resultante já é irredutível.
Frações com denominador diferente
Nesse caso, os adendos são substituídos por frações equivalentes com o mesmo denominador e, em seguida, o procedimento já descrito é seguido.
Exemplo
Adicione algebricamente os seguintes números racionais, simplificando o resultado:
Os passos são:
-Determine o múltiplo menos comum (lcm) dos denominadores 5, 8 e 3:
lcm (5,8,3) = 120
Este será o denominador da fração resultante sem simplificação.
-Para cada fração: divida o lcm pelo denominador e multiplique pelo numerador. O resultado desta operação é colocado, com seu respectivo sinal, no numerador da fração. Dessa maneira, é obtida uma fração equivalente ao original, mas com o cm3 como denominador.
Por exemplo, para a primeira fração, o numerador é construído assim: (120/5) x 4 = 96 e obtemos:
O mesmo procedimento é seguido para as frações restantes:
Finalmente, as frações equivalentes são substituídas sem esquecer o sinal e os numeradores são adicionados algebricamente:
(4/5) + (14/8) – (11/3) + 2 = (96/120) + (210/120) – (440/120) + (240/120) =
= (96 + 210-440 + 24) / 120 = -110 / 120 = -11/12
– Multiplicação e divisão
A multiplicação e a divisão são feitas seguindo as regras mostradas abaixo:
De qualquer forma, é importante lembrar que a multiplicação é comutativa, o que significa que a ordem dos fatores não altera o produto. Isso não acontece com a divisão, portanto, é preciso ter cuidado em respeitar a ordem entre dividendo e divisor.
Exemplo 1
Realize as seguintes operações e simplifique o resultado:
a) (5/3) x (15/8)
b) (-4/5) ÷ (2/9)
Responda para
(5/3) x (8/15) = (5 x 8) / (3 x 15) = 15/120 = 1/8
Resposta b
(-4/5) ÷ (2/9) = (-4 x 9) / (5 x 2) = -36 / 10 = -18/5
Exemplo 2
Luisa custava US $ 45. Ele passou a décima parte comprando um livro e 2/5 partes do que restava em uma camiseta. Quanto dinheiro resta à Luisa? Expresse o resultado em uma fração irredutível.
Solução
O custo do livro (1/10) x R $ 45 = 0,1 x R $ 45 = R $ 4,5
Portanto, Luisa ficou com:
45 – 4,5 $ = 40,5 $
Com esse dinheiro, Luisa foi à loja de roupas e comprou a camisa, cujo preço é:
(2/5) x R $ 40,5 = R $ 16,2
Agora Luisa tem em seu portfólio:
40,5 – $ 16,2 = $ 24,3
Para expressá-lo em fração, está escrito assim:
24,3 = 243/10
O que é irredutível.
Referências
- Baldor, A. 1986. Aritmética. Códice de Edições e Distribuições.
- Carena, M. 2019. Manual de Matemática. Universidade Nacional do Litoral.
- Figuera, J. 2000. Matemática 8. Ediciones Co-Bo.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Números racionais. Recuperado de: Summitnet.uoc.edu.
- Números racionais. Recuperado de: webdelprofesor.ula.ve.