A aceleração média é um conceito fundamental da física que mede a taxa de variação da velocidade de um objeto em determinado intervalo de tempo. Para calcular a aceleração média, é necessário conhecer a variação da velocidade e o intervalo de tempo em questão. A fórmula para calcular a aceleração média é dada pela variação da velocidade dividida pelo intervalo de tempo. Para resolver exercícios envolvendo aceleração média, é preciso identificar a velocidade inicial, a velocidade final e o intervalo de tempo, aplicando a fórmula adequada para encontrar o valor da aceleração média. A prática constante e a compreensão dos conceitos são essenciais para a resolução correta desses exercícios.
Calculando a média da aceleração: passo a passo para encontrar o valor correto.
Para calcular a média da aceleração, é necessário seguir alguns passos simples para encontrar o valor correto. A aceleração média é a taxa de variação da velocidade de um objeto em um determinado intervalo de tempo. Para calcular a média da aceleração, você precisa seguir os seguintes passos:
Passo 1: Determine a variação da velocidade do objeto. Isso pode ser feito subtraindo a velocidade final pela velocidade inicial.
Passo 2: Determine o intervalo de tempo em que ocorreu essa variação de velocidade. Isso pode ser calculado subtraindo o tempo final pelo tempo inicial.
Passo 3: Divida a variação da velocidade pelo intervalo de tempo para encontrar a aceleração média. A fórmula para calcular a aceleração média é: a = (vf – vi) / (tf – ti).
Por exemplo, se um carro aumentou sua velocidade de 20 m/s para 40 m/s em 5 segundos, a aceleração média pode ser calculada da seguinte forma: a = (40 – 20) / 5 = 4 m/s².
Seguindo esses passos simples, você poderá calcular com precisão a média da aceleração de um objeto em movimento. Pratique resolvendo exercícios para aprimorar suas habilidades e compreensão sobre o assunto.
Métodos para determinar a aceleração de um objeto em movimento uniformemente variado.
A aceleração de um objeto em movimento uniformemente variado pode ser determinada de diversas formas, utilizando métodos que envolvem o cálculo matemático e a análise de dados experimentais. Um dos métodos mais comuns para calcular a aceleração média de um objeto é através da fórmula da aceleração média, que é dada por:
a = (vf – vi) / t
Onde a representa a aceleração média, vf é a velocidade final do objeto, vi é a velocidade inicial do objeto e t é o intervalo de tempo considerado. Para resolver exercícios envolvendo a aceleração média, é necessário utilizar esta fórmula e substituir os valores conhecidos para encontrar o valor da aceleração.
Outro método comum para determinar a aceleração de um objeto em movimento uniformemente variado é através do gráfico da velocidade em função do tempo. Neste caso, a aceleração média pode ser calculada a partir da inclinação da reta tangente ao gráfico, utilizando a fórmula:
a = Δv / Δt
Onde Δv representa a variação da velocidade e Δt é a variação do tempo. Para resolver exercícios utilizando este método, basta identificar a inclinação da reta tangente ao gráfico e calcular a aceleração média a partir desta inclinação.
Em resumo, existem diferentes métodos para determinar a aceleração de um objeto em movimento uniformemente variado, seja através da fórmula da aceleração média ou da análise do gráfico da velocidade em função do tempo. Utilizando esses métodos, é possível calcular com precisão a aceleração de um objeto em movimento e resolver exercícios que envolvam este conceito.
Fórmula da aceleração escalar média: como calculá-la de forma simples e prática.
A aceleração média é uma grandeza vetorial que representa a variação da velocidade de um objeto em relação ao tempo. Ela é calculada pela fórmula da aceleração escalar média: a = Δv / Δt, onde a é a aceleração, Δv é a variação da velocidade e Δt é a variação do tempo.
Para calcular a aceleração média de forma simples e prática, basta seguir alguns passos. Primeiramente, você precisa determinar a velocidade inicial e final do objeto, bem como o intervalo de tempo em que ocorreu a variação de velocidade. Em seguida, subtraia a velocidade final pela inicial para encontrar a variação da velocidade. Por fim, divida essa variação pela variação do tempo para obter a aceleração média.
Por exemplo, se um carro parte do repouso e atinge a velocidade de 20 m/s em 5 segundos, podemos calcular a aceleração média da seguinte forma: Δv = 20 m/s – 0 m/s = 20 m/s e Δt = 5 s. Substituindo na fórmula, temos a = 20 m/s / 5 s = 4 m/s².
Dessa forma, a fórmula da aceleração escalar média é uma ferramenta fundamental para resolver problemas envolvendo o estudo da cinemática. Com ela, é possível determinar a taxa de variação da velocidade de um objeto ao longo do tempo, contribuindo para a compreensão do movimento e sua dinâmica.
Significado da aceleração média: conceito e definição fundamental para compreensão da física.
Significado da aceleração média: A aceleração média é uma grandeza vetorial que representa a variação da velocidade de um objeto em determinado intervalo de tempo. Em outras palavras, é a taxa de variação da velocidade em relação ao tempo. A aceleração média é fundamental para a compreensão da física, pois permite analisar e descrever o movimento dos corpos de maneira mais precisa.
Para calcular a aceleração média, utilizamos a fórmula:
a = Δv / Δt
Onde a representa a aceleração média, Δv é a variação da velocidade e Δt é a variação do tempo. A unidade de medida da aceleração no Sistema Internacional (SI) é o metro por segundo ao quadrado (m/s²).
Para resolver exercícios envolvendo aceleração média, é importante seguir alguns passos. Primeiramente, é necessário identificar as informações fornecidas, como a velocidade inicial, a velocidade final e o intervalo de tempo. Em seguida, aplicamos a fórmula da aceleração média e realizamos os cálculos necessários.
É importante ressaltar que a aceleração média pode ser positiva, quando o objeto está acelerando, ou negativa, quando o objeto está desacelerando. Além disso, a aceleração média também pode ser nula, indicando que o objeto está em movimento uniforme, ou seja, com velocidade constante.
Em resumo, a aceleração média é uma grandeza fundamental para a compreensão da física, pois permite analisar e descrever o movimento dos corpos de forma mais precisa. Ao compreender o conceito e a definição da aceleração média, torna-se mais fácil resolver exercícios e aplicar os conhecimentos em situações práticas do dia a dia.
Aceleração média: como são calculados e resolvidos os exercícios
A aceleração média para m é a magnitude que descreve a variação na velocidade de uma partícula ao longo do tempo. É importante, porque mostra as variações que o movimento experimenta.
Para expressar essa magnitude em termos matemáticos, é necessário considerar duas velocidades e dois instantes de tempo, respectivamente designados como v 1 e v 2 , e t 1 e t 2 .

Combinando os valores de acordo com a definição oferecida, a seguinte expressão será usada:
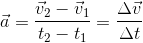
No sistema internacional SE, as unidades para um m serão m / s 2 , embora outras unidades que envolvem comprimento por unidade de tempo ao quadrado sirvam.
Por exemplo, há o km / h que lê “quilômetro por hora e por segundo”. Observe que a unidade de tempo aparece duas vezes. Pensar em um celular que viaja em linha reta significa que, a cada segundo decorrido, o celular aumenta sua velocidade em 1 km / h. Ou diminui em 1 km / h por cada segundo que passa.
Aceleração, velocidade e velocidade
Embora esteja associado à aceleração com um aumento na velocidade, a verdade é que, observando cuidadosamente a definição, verifica-se que qualquer alteração na velocidade implica na existência de uma aceleração.
E a velocidade nem sempre muda necessariamente em magnitude. Pode acontecer que o celular varie apenas na direção e mantenha a velocidade constante. Ainda existe uma aceleração responsável dessa mudança.
Um exemplo disso é um carro que faz uma curva com uma velocidade constante de 60 km / h. O veículo está sujeito a aceleração, responsável por alterar a direção da velocidade para que o carro siga a curva. O motorista o aplica usando o volante.
Essa aceleração é direcionada para o centro do caminho curvo, para que o carro não saia dele. É chamado aceleração radial ou normal . Se a aceleração radial fosse repentinamente cancelada, o carro não poderia mais continuar a curva e continuar em linha reta.
Um carro que se move ao longo de uma curva é um exemplo de movimento bidimensional, enquanto que quando está se movendo em uma linha reta, seu movimento é unidimensional. Nesse caso, o único efeito da aceleração é alterar a velocidade do carro.
Essa aceleração é chamada aceleração tangencial . Não é exclusivo do movimento unidimensional. O carro que dá a curva a 60 km / h pode acelerar simultaneamente a 70 km / h enquanto a leva. Nesse caso, o motorista precisa usar o volante e o pedal do acelerador.
Se considerarmos um movimento unidimensional, a aceleração média tem uma interpretação geométrica semelhante à da velocidade média, como uma inclinação da linha secante que corta a curva nos pontos P e Q do gráfico velocidade versus tempo.
Isso pode ser visto na figura a seguir:

Como a aceleração média é calculada
Vejamos alguns exemplos para calcular a aceleração média em várias situações:
I) Em um determinado momento, um móvel que viaja em linha reta tem uma velocidade de + 25 km / he 120 segundos depois tem outro de -10 km / h. Qual foi a aceleração média?
Resposta
Como o movimento é unidimensional, a notação vetorial pode ser dispensada; nesse caso:
v o = +25 km / h = +6,94 m / s
v f = -10 km / h = – 2,78 m / s
Δt = 120 s
Sempre que você faz um exercício com magnitudes mistas como essa, em que há horas e segundos, é necessário passar todos os valores para as mesmas unidades.
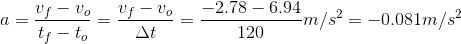
Sendo um movimento unidimensional, a notação vetorial foi dispensada.
II) Um ciclista viaja para leste a uma taxa de 2,6 m / se 5 minutos depois segue para o sul a 1,8 m / s. Encontre a sua aceleração média.
Resposta
O movimento não é unidimensional; portanto, é feito uso de notação vetorial. Os vectores unitários i e j indicam as direcções com a seguinte convenção sinal, facilitando o cálculo:
- Norte: + j
- Sul: – j
- Leste: + i
- Oeste: – i
v 2 = – 1,8 j m / s
v 1 = + 2,6 i m / s
Δt = 5 minutos = 300 segundos
Sinais de aceleração em movimento unidimensional
Como sempre com as magnitudes média ou média, as informações fornecidas são globais. Eles não oferecem detalhes do que aconteceu com o celular a cada momento, mas o que eles contribuem ainda é valioso para a descrição do movimento.
Através dos sinais de velocidade e aceleração, é possível saber se um celular que se move em linha reta acelera ou freia. Nas duas situações, a aceleração está presente, pois a velocidade está mudando.
Estas são algumas considerações interessantes sobre os sinais dessas duas magnitudes:
- Velocidade e aceleração médias, ambas do mesmo sinal, significa que, visto globalmente, o celular está cada vez mais rápido.
- Velocidade e aceleração com sinais diferentes é um sinal móvel tem diminuído bastante.
Pensa-se frequentemente que sempre que há uma aceleração negativa, o celular está travando. Isso é verdade se a velocidade do celular for positiva. Mas se for negativo, de fato a velocidade está aumentando.
Como sempre, quando o movimento é estudado, casos especiais são considerados. Por exemplo, o que acontece quando a aceleração média é zero? Isso significa que o celular sempre manteve sua velocidade constante?
A resposta é não. O celular poderia ter variado sua velocidade no intervalo considerado, mas a velocidade inicial e final eram as mesmas. No momento, os detalhes do que aconteceu no intervalo são desconhecidos, pois a aceleração média não oferece mais informações.
E se a aceleração média a m for igual à aceleração a em qualquer ponto do intervalo de tempo? Essa é uma situação muito interessante chamada Movimento Retilíneo Uniformemente Variado ou MRUV por sua sigla.
Isso significa que a velocidade muda uniformemente ao longo do tempo. Portanto, a aceleração é constante. Na natureza existe esse movimento, com o qual todos estão familiarizados: a queda livre.
Queda livre: um movimento com aceleração constante
É sabido que a Terra atrai os objetos em direção ao seu centro e que, ao liberar alguns a uma certa altura, experimenta a aceleração da gravidade, cujo valor é aproximadamente constante e igual a 9,8 m / s 2 próximo à superfície.
Se a resistência do ar não interferir, o movimento é vertical e é conhecido como queda livre. Quando a aceleração é constante e escolhendo t 0 = 0, a equação da aceleração média é transformada em:
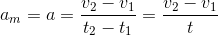
v f = v 0 + em = gt (v 0 = 0)
Onde a = g = 9,8 m / s 2
Exercício resolvido
Um objeto cai de uma altura suficiente. Encontre a velocidade após 1,25 segundos.
Resposta
v o = 0, desde que o objeto foi descartado, então:
v f = gt = 9,8 x 1,25 m / s = 12,25 m / s, direcionado verticalmente em direção ao solo. (A direção vertical foi reduzida como positiva).
À medida que o objeto se aproxima do solo, sua velocidade aumenta em 9,8 m / s por cada segundo decorrido. A massa do objeto não está envolvida. Dois objetos diferentes, caídos da mesma altura e ao mesmo tempo, desenvolvem a mesma velocidade em que caem.
Referências
- Giancoli, D. Física. Princípios com aplicações. Sexta Edição . Prentice Hall. 21-35.
- Resnick, R. (1999). Física Volume 1. Terceira edição em espanhol . México Empresa Editorial Continental SA de CV 20-34.
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. 7 ma . Edição . México Cengage Learning Publishers. 21-39.