A remoção da área de um pentágono envolve o cálculo da medida de sua base e altura, a fim de determinar a fórmula correta para encontrar a área total. Com base nas dimensões fornecidas, o processo de remoção pode ser feito através de várias fórmulas matemáticas, como a fórmula do pentágono regular, que considera o comprimento do lado do pentágono, ou a fórmula do pentágono irregular, que leva em conta as medidas individuais dos lados e ângulos do polígono. A remoção da área de um pentágono pode ser um processo desafiador, mas com o uso correto das fórmulas matemáticas adequadas, é possível obter o resultado preciso.
Como calcular a área de um pentágono: passo a passo para encontrar a medida correta.
Para calcular a área de um pentágono, é necessário seguir alguns passos simples. Primeiramente, identifique a medida do lado do pentágono, que chamaremos de l. Em seguida, utilize a fórmula para encontrar a área do pentágono, que é:
Área = (5/4) x l² x cot(π/5)
Substitua o valor de l na fórmula e calcule o resultado final. Assim, você terá a medida correta da área do pentágono.
Agora, vamos abordar o processo de remoção da área do pentágono. Para remover a área de um pentágono de uma figura maior, basta calcular a área do pentágono conforme mencionado anteriormente e subtrair essa medida da área total da figura. Dessa forma, você obterá a área restante após a remoção do pentágono.
Seguindo esses passos simples, você conseguirá calcular a área de um pentágono e também saber como é removida essa área de uma figura maior. Lembre-se de utilizar a fórmula correta e substituir os valores de maneira precisa para obter resultados precisos.
Como determinar as dimensões de um pentágono de forma simples e eficiente.
Para determinar as dimensões de um pentágono de forma simples e eficiente, podemos utilizar uma fórmula matemática específica. Um pentágono possui cinco lados iguais, portanto, para encontrar o comprimento de cada lado, podemos dividir o perímetro total do pentágono por 5. Por exemplo, se o perímetro total do pentágono for 20 cm, cada lado terá 4 cm de comprimento.
Além disso, para encontrar a medida do ângulo interno de um pentágono regular, podemos utilizar a fórmula 180 * (n – 2) / n, onde n é o número de lados do polígono. No caso de um pentágono, o ângulo interno será de 108 graus.
Como é removida a área do Pentágono?
Para calcular a área de um pentágono, podemos utilizar a fórmula (Perímetro * Apótema) / 2, onde o apótema é a distância do centro do pentágono até qualquer um de seus lados. Uma vez que tenhamos calculado a área do pentágono, podemos remover essa área de diferentes maneiras, como cortando o pentágono em formas menores ou preenchendo a área com outra forma geométrica.
Portanto, com essas fórmulas e métodos simples, podemos determinar as dimensões de um pentágono e remover sua área de maneira eficiente.
Significado e cálculo da apótema em uma figura geométrica de cinco lados.
Na geometria, a apótema é a medida da distância do centro de uma figura geométrica até um dos lados, sendo perpendicular a esse lado. No caso de um pentágono, a apótema é a medida da distância do centro até um dos lados do pentágono regular.
Para calcular a apótema de um pentágono regular, podemos utilizar a fórmula:
apótema = lado / (2 * tan(180° / n))
Onde lado é o comprimento de um dos lados do pentágono e n é o número de lados da figura, que no caso do pentágono é 5.
Uma vez que a apótema é calculada, podemos utilizá-la para encontrar a área do pentágono. A área de um pentágono regular pode ser calculada pela fórmula:
área = (perímetro * apótema) / 2
Assim, removendo a área de um pentágono, podemos calcular a área restante da figura. Este cálculo é útil em diversas aplicações, como na arquitetura, na engenharia e na matemática.
Aprenda a calcular o perímetro de um pentágono de forma simples e prática.
Aprender a calcular o perímetro de um pentágono é mais simples do que parece. Para isso, basta somar os comprimentos de todos os lados do pentágono. Um pentágono possui cinco lados iguais, então para encontrar o perímetro, basta multiplicar o comprimento de um lado por cinco.
Por exemplo, se o comprimento de um lado do pentágono for de 3 cm, o perímetro será de 3 x 5 = 15 cm. Portanto, o perímetro do pentágono será de 15 centímetros.
Lembrando que o perímetro é a medida total da borda do pentágono, ou seja, a soma de todos os lados.
Como é removida a área do Pentágono?
Para remover a área de um pentágono, é necessário calcular a medida da área total do pentágono e subtrair a medida da área que deseja ser removida. A fórmula para calcular a área de um pentágono regular é:
Área = (Perímetro x Apótema) / 2
Onde o perímetro é a soma dos comprimentos de todos os lados e o apótema é a distância do centro do pentágono até o meio de um dos lados. Para remover a área desejada, basta subtrair essa medida da área total do pentágono.
Com esses simples cálculos, é possível calcular o perímetro e remover a área de um pentágono de forma prática e eficiente.
Como é removida a área do Pentágono?
A área de um pentágono é calculada usando um método conhecido como triangulação, que pode ser aplicado a qualquer polígono. Este método consiste em dividir o pentágono em vários triângulos.
Depois disso, a área de cada triângulo é calculada e, finalmente, todas as áreas encontradas são adicionadas. O resultado será a área do pentágono.

O pentágono também pode ser dividido em outras formas geométricas, como um trapézio e um triângulo, como a figura à direita.
O problema é que o comprimento da base principal e a altura do trapézio não são fáceis de calcular. Além disso, a altura do triângulo vermelho deve ser calculada.
Como calcular a área de um pentágono?
O método geral para calcular a área de um pentágono é a triangulação, mas o método pode ser direto ou um pouco mais longo, dependendo se o pentágono é regular ou não.
Área de um pentágono regular
Antes de calcular a área, é necessário saber qual é o apótema.
O apótema de um pentágono regular (polígono regular) é a distância mais curta do centro do pentágono (polígono) até o ponto médio de um lado do pentágono (polígono).
Em outras palavras, o apótema é o comprimento do segmento de linha que vai do centro do pentágono ao ponto médio de um lado.

Considere um pentágono regular, de modo que o comprimento de seus lados seja “L”. Para calcular seu apótema, primeiro divida o ângulo central α pelo número de lados, ou seja, α = 360º / 5 = 72º.
Agora, usando as relações trigonométricas, o comprimento do apótema é calculado como mostrado na imagem a seguir.

Portanto, o apótema tem um comprimento de L / 2tan (36º) = L / 1,45.
Quando você realiza a triangulação do pentágono, obtém uma figura como a abaixo.

Os 5 triângulos têm a mesma área (por ser um pentágono regular). Portanto, a área do pentágono é 5 vezes a área de um triângulo. Ou seja: área de um pentágono = 5 * (L * ap / 2).
Substituindo o valor do apótema, a área é A = 1,72 * L².
Portanto, para calcular a área de um pentágono regular, você só precisa saber o comprimento de um lado.
Área de um pentágono irregular
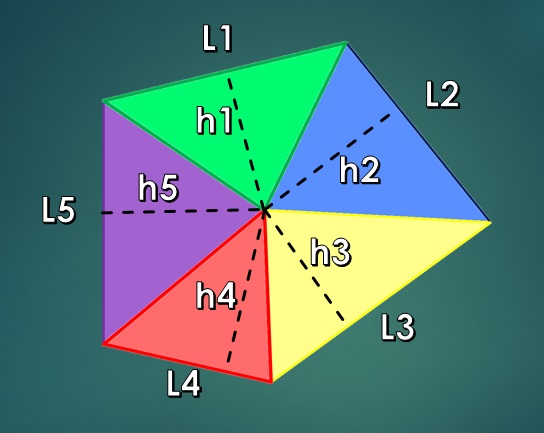
Começa a partir de um pentágono irregular, de modo que os comprimentos de seus lados sejam L1, L2, L3, L4 e L5. Nesse caso, o apótema não pode ser usado como antes.
Depois de fazer a triangulação, você obtém uma figura como a seguinte:

Agora, vamos desenhar e calcular as alturas desses 5 triângulos interiores.
Então, as áreas dos triângulos internos são T1 = L1 * h1 / 2, T2 = L2 * h2 / 2, T3 = L3 * h3 / 2, T4 = L4 * h4 / 2 e T5 = L5 * h5 / 2.
Os valores correspondentes a h1, h2, h3, h4 e h5 são as alturas de cada triângulo, respectivamente.
Finalmente, a área do pentágono é a soma dessas 5 áreas. Ou seja, A = T1 + T2 + T3 + T4 + T5.
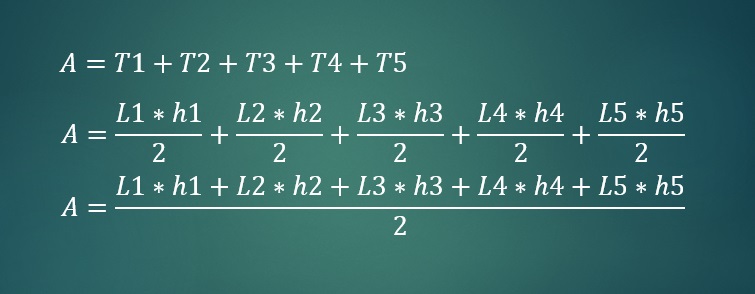
Como pode ser visto, calcular a área de um pentágono irregular é mais complexo do que calcular a área de um pentágono regular.
Determinante de Gauss
Há também outro método pelo qual você pode calcular a área de qualquer polígono irregular, conhecido como determinante de Gauss.
Este método consiste em desenhar o polígono no plano cartesiano, e as coordenadas de cada vértice são calculadas.
Os vértices são enumerados no sentido anti-horário e, finalmente, determinados determinantes são calculados para finalmente obter a área do polígono em questão.

Referências
- Alexander, DC, e Koeberlein, GM (2014). Geometria elementar para estudantes universitários. Cengage Learning
- Arthur Goodman, LH (1996). Álgebra e trigonometria com geometria analítica. Pearson Education.
- Lofret, EH (2002). O livro de tabelas e fórmulas. Imaginator
- Palmer, CI, & Bibb, SF (1979). Matemática prática: aritmética, álgebra, geometria, trigonometria e regra de cálculo (reimpressão). Reverte
- Posamentier, AS e Bannister, RL (2014). Geometria, seus elementos e estrutura: segunda edição. Courier Corporation.
- Quintero, AH, & Costas, N. (1994). Geometria O Editorial, UPR.
- Ruiz, Á .; Barrantes, H. (2006). Geometrias Editorial Tecnologica de CR.
- Torá, FB (2013). Matemática 1ª unidade de ensino 1º ESO, Volume 1. Editorial Club Universitario.
- Víquez, M., Arias, R. e Araya, J. (sf). Matemática (sexto ano). EUNED