Como elevar frações a termos maiores: expoentes fracionários sem mistério

Início » Ciência » Matemática » Como elevar frações a termos maiores: expoentes fracionários sem mistério

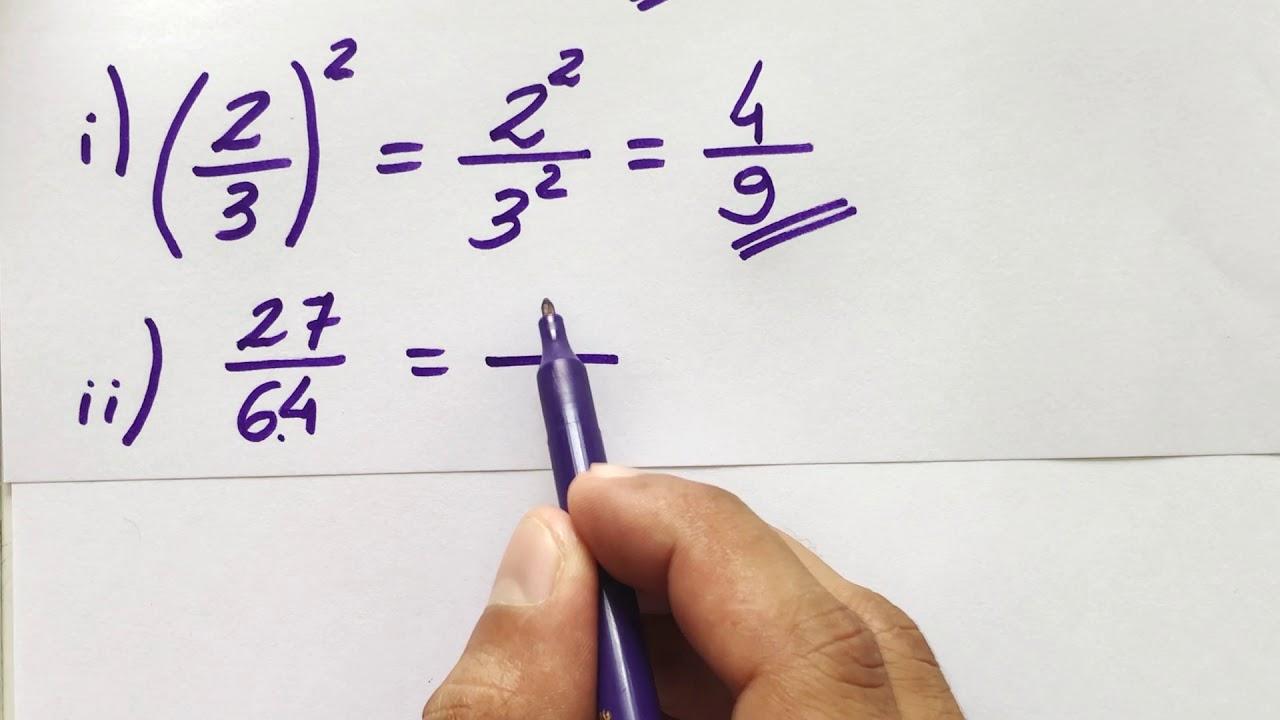
Quando o assunto é elevar frações a termos maiores e lidar com expoentes fracionários, muita gente pensa que é um bicho de sete cabeças, mas a verdade é que, com algumas conexões simples, tudo fica bem mais claro. ponte entre potenciação e radiciação, e entender essa relação abre várias portas na matemática do dia a dia e em provas.

Antes de mergulhar nos exemplos, vale destacar a ideia central: expoente é uma fração. Essa definição permite que a gente traduza a potência em uma raiz, tornando o cálculo mais direto, sem sustos. Segue comigo que vamos conectar as peças e, de quebra, revisar regras importantes de potências, negativos, decimais e casos com frações como base.

O que é um expoente fracionário e como ele funciona

Comecemos pelo conceito formal para deixar tudo redondinho. b^n/d na qual b é um número real (a base) e n/d é um número racional (o expoente) com n e d inteiros e d > 0. Esse tipo de potência pode ser reescrita como uma raiz, o que facilita muito o cálculo.

A conexão entre potência e raiz é a seguinte: b^n/d = raiz d-ésima de bⁿ. Em outras palavras, o denominador do expoente vira o índice da raiz, e o numerador permanece como potência do radicando. Alternativamente, também vale b^n/d = (raiz d-ésima de b)ⁿ, o que às vezes simplifica ainda mais a conta.

Para ficar concreto, pegue um expoente como 3/2: b^3/2 = √(b³) ou (√b)³. Dependendo do valor de b, uma das formas costuma ser mais prática que a outra.

Existe um detalhe importante quanto ao domínio: d par exige b ≥ 0. Por exemplo, b^1/2 (raiz quadrada) só é real se b ≥ 0; já em b^1/3, como o índice é ímpar, dá para trabalhar com b negativo também.

Regras básicas de potenciação que continuam valendo

Apesar do aspecto novo do expoente fracionário, todas as propriedades usuais de potências seguem válidas quando respeitadas as condições de existência. Isso significa que:

• Produto de mesma base: b^r · b^s = b^r+s.
• Quociente de mesma base: b^r / b^s = b^r−s, com b ≠ 0.
• Potência de potência: (b^r)^s = b^r·s.
• Potência de produto: (ab)^r = a^r·b^r.
• Potência de quociente: (a/b)^r = a^r/b^r, com b ≠ 0.

Além disso, as potências notáveis também ajudam: b^−k = 1/b^k. Esta última é valiosa para expoentes negativos, inclusive quando o expoente é racional.

Transformando expoente fracionário em raiz: passo a passo

Quando aparecer uma fração no expoente, a receita é direta. Identificar numerador e denominador e seguir as etapas abaixo facilita a transição para raiz.

1. Identifique o numerador (n) e o denominador (d) do expoente racional.
2. Converta o denominador em índice de raiz: b^n/d vira raiz d-ésima.
3. Mantenha o numerador como potência: b^n/d = √(bⁿ).
4. Opcionalmente, inverta a ordem: b^n/d = (√(b))ⁿ, caso isso simplifique o cálculo.
5. Verifique o domínio: se d for par, garanta b ≥ 0 para permanecer no conjunto dos reais.

Essa reescrita é o coração do método: forma compacta de escrever raízes, e mover de um formato ao outro é o que destrava as contas.

Exemplos essenciais para fixar a ideia

Vamos aquecer com um exemplo clássico de potência inteira antes de entrar nas frações. 3⁵ = 243, o que dá 3 · 3 · 3 · 3 · 3 = 243. Essa observação lembra que o expoente indica o número de repetições da base em um produto.

Outro ponto que não pode faltar: expoente negativo = inverso da potência. Por exemplo, 2⁻³ = 1/2³ = 1/8. Isso também se estende a expoentes racionais, como veremos mais adiante.

Agora, mergulhando de vez nos fracionários, consideremos um caso geral com a, x e y inteiros (y > 0) e a real: a^x/y = √(a^x), respeitando as condições de existência para a raiz. Essa é a forma padrão de interpretar potências com expoente fracionário.

Segura aí que tem muito mais vindo; a ideia vai clareando. Acompanhe a sequência a seguir, numerada como em muitos materiais didáticos, para organizar melhor as técnicas.

1º Exemplo: Calcule 27^2/3.
Escolha a forma mais conveniente: (√(27))² = 3² = 9. 27 é um cubo perfeito, extrair a raiz primeiro simplifica.

2º Exemplo: Calcule 16^3/4.
Escreva como (√(16))³ = 2³ = 8, já que 16 é uma potência de 2 e sua raiz quarta é 2. aplicar a raiz antes da potência torna a conta direta.

3º Exemplo: Calcule 9^3/2.
Podemos fazer (√(9))³ = 3³ = 27. Alternativamente, √(9³) = √(729) = 27. ambas as abordagens conduzem ao mesmo resultado.

4º Exemplo: Calcule (9/16)^1/2.
Como (a/b)^r = a^r/b^r, temos (9/16)^1/2 = √(9)/√(16) = 3/4. raízes de frações são especialmente simples quando numerador e denominador são quadrados perfeitos.

5º Exemplo: Expoente negativo e fracionário: 25^−1/2.
Primeiro lide com o sinal: 25^−1/2 = 1/25^1/2 = 1/√(25) = 1/5. sinal negativo inverte a potência e o denominador fracionário vira raiz.

6º Exemplo: Base fracionária e expoente racional: (81/16)^3/4.
Escreva como (√(81)/√(16))³ = (3/2)³ = 27/8. separar numerador e denominador permite contas tranquilas com potências e raízes.

Elevando frações a termos maiores

Quando a base já é uma fração, as propriedades continuam jogando a nosso favor. Para (p/q)ⁿ, elevamos numerador e denominador separadamente: (p/q)ⁿ = pⁿ/qⁿ. Isso também vale quando n é fracionário, desde que as raízes existam no conjunto dos reais.

Por exemplo, (9/25)^1/2 = √(9)/√(25) = 3/5. índice par exige numerador e denominador não negativos para que o resultado seja real.

Para termos maiores (expoentes grandes), vale buscar simplificações prévias: fatore numerador e denominador, reduza a fração se possível, e identifique potências perfeitas. Assim, (32/81)^5/4 pode ser reescrita como ((2⁵)/(3⁴))^5/4 = (2^25/4)/(3⁵) e, em seguida, (√(32))⁵/243 = (2·√(2))⁵/243, se a ideia for manter o resultado exato.

Outra estratégia esperta: use a propriedade potência de potência quando a base já está como raiz. Por exemplo, (√(x))⁶ = x^6/4 = x^3/2 = (√x)³. Essa alternância de formas encurta o cálculo em muitas situações.

Expoentes decimais: transforme em fração

Decimais no expoente seguem a mesma lógica dos racionais. Converta o decimal em fração geratriz e, então, aplique o procedimento de raízes. Essa equivalência funciona inclusive quando o decimal não é dízima periódica, desde que você aceite resultados aproximados quando a fração geratriz não for exata no conjunto dos racionais finitos.

Por exemplo, 0,5 = 1/2. Logo, b^0,5 = b^1/2 = √b (com b ≥ 0). Da mesma forma, 0,75 = 3/4. Portanto, b^0,75 = b^3/4, quando a raiz quarta estiver definida.

Exemplo com decimal 0,5: 25^0,5 = √(25) = 5. Aqui, o expoente decimal foi convertido em fração, e a potência virou raiz.

Exemplo com decimal 0,75: 16^0,75 = 16^3/4 = (√(16))³ = 2³ = 8. quando a base é uma potência perfeita, o cálculo flui naturalmente.

Como resolver potências com expoente fracionário: guia rápido

Para não se perder no caminho, vale um pequeno roteiro prático. Ao ver um expoente fracionário, identifique o denominador (índice da raiz) e o numerador (potência) e escolha a ordem mais conveniente:

• Raiz primeiro, depois potência: útil quando a raiz da base é um número inteiro simples.
• Potência primeiro, depois raiz: vantajoso quando elevar a base ao numerador gera uma potência perfeita do índice.
• Separar fatores: em produtos e quocientes, distribua a potência para simplificar numerador e denominador.

Esse método funciona igualmente para bases fracionárias, números inteiros e expressões algébricas. o segredo é enxergar a estrutura da conta e atacar pelo lado que simplifica.

Expoente negativo: fracionário e fácil

Não precisa torcer o nariz para o sinal negativo no expoente. Regra: b^−r = 1/b^r, com b ≠ 0. Se r = n/d, então b^−n/d = 1/b^n/d = 1/√(bⁿ), assumindo que a raiz exista no conjunto dos reais.

Exemplo rápido: 36^−1/2 = 1/6. Se a base for uma fração, como (4/9)^−1/2, então (4/9)^−1/2 = 1/(4/9)^1/2 = 1/(2/3) = 3/2. inverter antes ou depois de extrair a raiz dá no mesmo.

Domínio, sinais e cuidados com raízes

Para manter o resultado real, observe as restrições; para casos que envolvam resultados não reais, consulte números imaginários. Se o índice da raiz for par, a base deve ser não negativa. Índices ímpares permitem base negativa. Assim, (−8)^1/3 = −2 é permitido, mas (−8)^1/2 não é real.

Outro cuidado: raízes pares de potências pares exigem atenção ao sinal. Embora (√(b²)) = |b| em contexto real, quando a expressão é b^2/2 = b, pressupõe-se b ≥ 0 para manter a equivalência simples. Esse tipo de detalhe costuma ser cobrado em contextos mais formais.

Quando trabalhar com simplificações simbólicas, sempre confira: a equivalência b^n/d = √(bⁿ) é correta, mas a volta pode exigir condições extras dependendo do sinal de b e se d é par ou ímpar.

Aplicando propriedades com frações e racionais

As propriedades de soma e subtração de expoentes continuam sendo aliadas. Por exemplo, a^1/2 · a^1/3 = a^5/6, assumindo a > 0. De modo similar, a¹ / a^1/4 = a^3/4. Essa manipulação ajuda a compor e decompor expoentes para facilitar raízes.

Para quocientes, separar os termos ainda é uma ótima pedida. (a/b)^m/n = a^m/n/b^m/n, garantindo b ≠ 0 e observando o domínio das raízes. Com bases fatoradas, identifique potências perfeitas para reduzir o esforço.

Em expressões algébricas, essas regras dão a mesma tração. (x⁶)^1/3 = x², desde que x seja real. E (x³y⁴)^1/2 = x^3/2y², o que às vezes pode ser reescrito como y²·(√(x³)) = y²·x·√x, dependendo do contexto e da necessidade de simplificação.

Mais exemplos comentados (do básico ao elaborado)

Exemplo A: 81^1/2.
√(81) = 9. quadrado perfeito, conta direta.

Exemplo B: 125^2/3.
(√(125))² = 5² = 25. cubo perfeito simplifica ao extrair a raiz primeiro.

Exemplo C: (64/27)^−2/3.
Inverta e depois aplique a potência: (64/27)^−2/3 = (27/64)^2/3 = ((√(27))/ (√(64)))² = (3/4)² = 9/16. ordem das operações reduz a complexidade.

Exemplo D: 32^3/5.
(√(32))³ = 2³ = 8, pois 32 = 2⁵. raiz de potência perfeita é atalho.

Exemplo E: (9/4)^1,5.
Converta 1,5 para 3/2: (9/4)^3/2 = ((√(9))/ (√(4)))³ = (3/2)³ = 27/8. decimais no expoente via fração geratriz.

Exemplo F: 10⁰ e 10^−1/2.
10⁰ = 1. Já 10^−1/2 = 1/10^1/2 = 1/√(10). zero no expoente e expoente negativo mantêm suas regras clássicas.

Erros comuns e como evitá-los

Alguns deslizes aparecem com frequência e custam pontos à toa. O primeiro é esquecer que o denominador do expoente é o índice da raiz. Não confunda b^n/d com √(b)^n/d sem ajustar corretamente a ordem das operações.

Outro tropeço comum é ignorar o domínio. Para raízes pares, a base precisa ser não negativa. Esquecer disso pode levar a conclusões erradas, especialmente quando simplificando expressões algébricas.

Também vale lembrar: b^−r não é −b^r. O sinal negativo do expoente atua no denominador (inverso), não no sinal da base. Apenas se a base for negativa e o expoente tiver numerador ímpar é que o resultado poderá ser negativo, respeitando a existência da raiz.

Por fim, não caia na armadilha de simplificar radical de soma ou subtração como se fosse soma de radicais. √(a + b) ≠ √a + √b, regra que continua valendo quando se manipula potências fracionárias via raízes.

Dicas para resolver mais rápido

Para ganhar agilidade, crie o hábito de reconhecer padrões. Potências perfeitas facilitam. Por exemplo, 64, 81, 125 e 256 são bons candidatos para raízes de índices pequenos.

Outra dica é decompor a base em fatores primos, quando necessário. Escrever a base como produto de potências permite aplicar a regra (ab)^r = a^rb^r e simplificar parte por parte.

Em frações, reduza antes. Simplificar numerador e denominador com divisores comuns pode transformar o exercício, deixando-o muito mais curto.

E, claro, pratique com contas que você consiga fazer mentalmente. Assim, quando aparecer algo maior, você já terá um repertório de atalhos e reconhecerá a melhor abordagem quase de imediato.

Um olhar rápido sobre exercícios típicos

Vários materiais didáticos apresentam baterias de exercícios semelhantes aos que vimos. É comum ver instruções como “resolva as potências com expoente fracionário” seguidas de itens com bases inteiras, fracionárias e até expressões com letras.

Em alguns casos, existe uma dinâmica de “veja a resposta” após cada item. Se você estiver estudando sozinho, tente fazer sem olhar, depois confira o gabarito. Essa prática ajuda a consolidar o método de transformação em raiz e o uso das propriedades de potências.

Se aparecerem notas do tipo “segure um pouco, já continua”, encare como uma pausa para assimilar. Um pequeno intervalo ajuda a fixar o raciocínio de que frações no expoente equivalem a raízes e de que expoentes negativos pedem inversão.

Checklist mental para não errar

Antes de concluir qualquer questão, passe os olhos por um mini-checklist. Verificou o domínio do radical (especialmente se o índice é par)? Se sim, prossiga confiante.

Você escolheu a ordem mais vantajosa: raiz antes de potência ou potência antes de raiz? Essa decisão costuma economizar tempo de forma significativa.

As propriedades foram aplicadas corretamente (produto, quociente, potência de potência)? Uma checagem rápida evita erros bobos de sinal e de fração.

E, por fim, confira se a resposta pode ser reduzida (por exemplo, fracionária simplificada ou raiz transformada em potência racional equivalente).

Aprender a elevar frações a termos maiores e a lidar com expoentes fracionários é, no fundo, uma questão de tradução entre linguagens da mesma operação. Quando você enxerga b^n/d como uma raiz d-ésima de bⁿ, a conta ganha estrutura e o medo vai embora. Mantendo as regras de potência, o cuidado com domínios e a prática com exemplos típicos (incluindo negativos e decimais), o caminho fica muito mais suave no caderno e nas provas.