Como Resolver Problemas Matemáticos com Frações Passo a Passo

Início » Ciência » Matemática » Como Resolver Problemas Matemáticos com Frações Passo a Passo

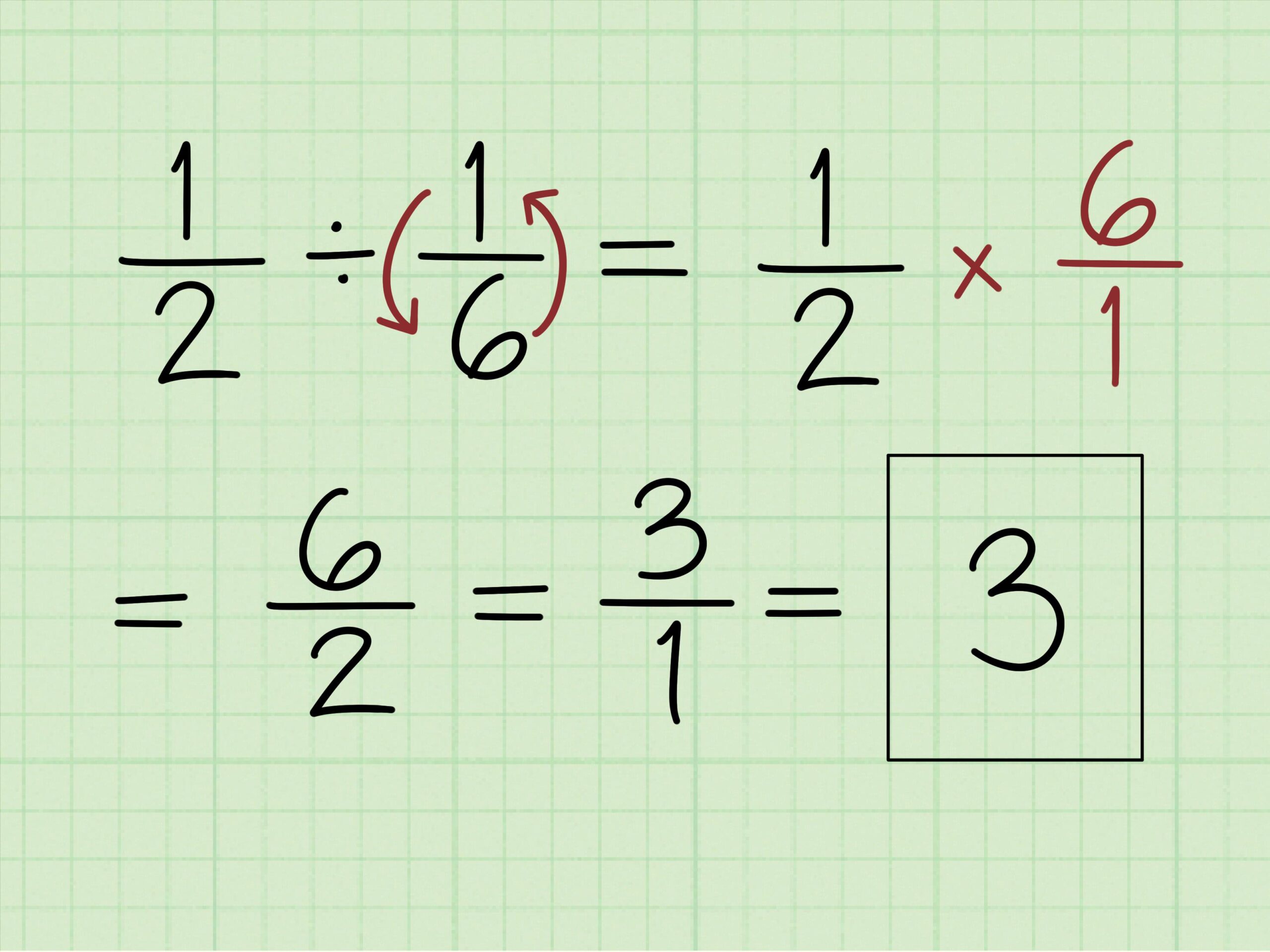
Resolver problemas matemáticos com frações assusta muita gente, mas, na prática, boa parte dessas questões segue sempre o mesmo tipo de raciocínio. Aparecem em provas escolares, vestibulares, concursos e até em situações do dia a dia, como receitas de cozinha, contas de casa, divisão de contas ou análise de gráficos. Quando você entende bem como funcionam as operações com frações e sabe interpretar o enunciado, essas questões deixam de ser um bicho de sete cabeças e viram quase um roteiro automático.

Ao longo deste artigo, você vai ver como atacar problemas com frações de forma organizada, relembrar as regras de adição, subtração, multiplicação, divisão e simplificação, descobrir os tipos de fração mais cobrados e praticar com vários exemplos comentados. A ideia é juntar tudo: explicações passo a passo, exercícios resolvidos e questões em formato de múltipla escolha, muito parecidas com as que caem em provas importantes como o Enem e vestibulares de grandes universidades.

Por que dominar problemas com frações é tão importante?

Frações aparecem em praticamente todos os níveis de Matemática escolar e são uma porta de entrada para conteúdos como porcentagem, razões, proporções e até probabilidade. Quando você entende bem uma fração, passa a enxergá-la como uma forma de representar partes de um todo, seja esse todo um número, uma quantidade de litros, metros, alunos, dinheiro ou qualquer outra grandeza.

Em contexto escolar, problemas com frações ajudam a desenvolver o raciocínio lógico e a interpretação de texto matemático. Não é só conta: é ler, entender o cenário, transformar o que está escrito em uma expressão numérica, escolher a operação correta e, por fim, analisar se o resultado faz sentido. Esse ciclo é exatamente o que mais aparece em avaliações e provas oficiais.

No cotidiano, frações estão em rótulos de produtos, receitas, repartição de contas, descontos e estatísticas. Quando um enunciado diz que “2/9 dos alunos ficaram em recuperação” ou que “3/5 de uma turma não usa óculos”, você está lidando com frações que representam parcelas de uma quantidade total. Saber calcular “quanto isso vale” e “quanto falta para completar o todo” é fundamental.

Outro ponto crucial é que, em provas de múltipla escolha, a resposta costuma ser cobrada em forma irredutível. Isso quer dizer que, muitas vezes, mais do que chegar à fração certa, é necessário ainda simplificá-la dividindo numerador e denominador por um mesmo número, até não ser mais possível reduzir, garantindo que você encontre exatamente a alternativa correta.

Regras básicas: como operar com frações em problemas

Antes de encarar problemas mais elaborados, vale relembrar de forma bem direta as regras das quatro operações com frações. Essas regras vão ser usadas em praticamente todos os exercícios que aparecem ao longo do texto.

Na adição e subtração de frações com mesmo denominador, o procedimento é bem tranquilo: você mantém o denominador e soma ou subtrai apenas os numeradores. Por exemplo, em 3/8 + 2/8, basta fazer 3 + 2 no numerador e conservar o 8 embaixo, obtendo 5/8. O denominador indica em quantas partes o todo foi dividido; como ele é o mesmo, somar ou tirar partes fica direto.

Quando os denominadores são diferentes, primeiro é preciso deixá-los iguais, normalmente usando o mínimo múltiplo comum (MMC). Depois disso, transforma-se cada fração em uma equivalente com o novo denominador comum e só então se somam ou subtraem os numeradores. Em 3/5 – 1/4, por exemplo, o MMC de 5 e 4 é 20; transformamos 3/5 em 12/20 e 1/4 em 5/20, e então a conta vira 12/20 – 5/20 = 7/20.

Na multiplicação de frações, a regra é ainda mais simples: multiplica-se numerador com numerador e denominador com denominador. Se você tiver 2/5 × 3/7, faz 2 × 3 = 6 no numerador e 5 × 7 = 35 no denominador, resultando em 6/35. Muitas vezes ainda é possível simplificar, caso numerador e denominador tenham algum fator comum.

Na divisão entre frações, usamos a ideia de multiplicar pela fração inversa da segunda. Isso significa que, em vez de dividir por uma fração, você multiplica pela sua recíproca (inverte numerador e denominador). Em 4/5 ÷ 7/2, por exemplo, calculamos 4/5 × 2/7, o que dá 8/35 depois de multiplicar cruzado numeradores e denominadores.

Em qualquer operação, simplificar a fração final é um passo essencial, especialmente em exercícios de prova. Para simplificar, basta dividir numerador e denominador pelo maior divisor comum (ou, se preferir, ir dividindo por fatores comuns como 2, 3, 5 etc. até não dar mais). Assim, 35/50 pode ser simplificado dividindo ambos por 5, chegando a 7/10.

Passo a passo para resolver problemas com frações

Resolver problemas com frações não é só aplicar fórmulas, mas seguir uma rotina de leitura, interpretação e cálculo. Seguindo uma sequência organizada, fica bem mais fácil não se perder no meio do caminho.

O primeiro passo é ler o enunciado com calma e, se necessário, mais de uma vez. É fundamental identificar quem são os personagens, quais são os dados numéricos fornecidos (frações, totais, quantidades em litros, metros, dinheiro, número de alunos) e, principalmente, o que está sendo perguntado. Às vezes a questão pede diretamente a fração; em outras, o valor correspondente em unidades.

Em seguida, identifique as frações envolvidas e quais operações aparecem na situação descrita. Alguns problemas pedem que você some ou subtraia partes de um todo (como gastos de salário, quantidades de comida, partes de um caminho já percorridas), outros exigem multiplicar uma fração por um número inteiro (como “3/4 de 16” ou “2/5 de 18 000”) e, em certas questões, é necessário resolver uma pequena equação com frações.

Depois de escolher a operação, monte a expressão numérica que representa o problema. Isso pode ser algo como 1 – 3/4, 2/5 × 18 000, 3/4 + 1/6 + 1/5 ou uma equação do tipo x – 2/5 x – 1/2 x = 34. Escrever essa expressão de forma organizada ajuda a visualizar o que fazer passo a passo, sem pular nenhuma parte do raciocínio.

Na hora do cálculo, aplique as regras de frações com atenção aos denominadores e à simplificação. Não se esqueça de igualar denominadores em somas e subtrações, de inverter a segunda fração em divisões e de multiplicar numeradores e denominadores nas multiplicações. Ao final, verifique se o resultado pode ou deve ser escrito como fração irredutível.

Por fim, faça a interpretação da resposta: confira se o número encontrado combina com o contexto do problema. Se a pergunta é sobre “quantos alunos” ou “quantos litros”, o resultado precisa ser coerente, não pode ser negativo ou maior do que o total, e, em geral, deve ser um número inteiro. Se a pergunta pede a fração que representa uma parte, verifique se ela é menor ou igual a 1, dependendo do contexto.

Tipos de frações mais cobrados em provas

Ao estudar problemas com frações, é muito útil reconhecer rapidamente o tipo de fração que você está usando, porque isso ajuda a prever o comportamento do número. Saber se uma fração é menor que 1, maior que 1 ou corresponde a um número inteiro faz diferença na hora de interpretar enunciados.

Chamamos de fração própria aquela em que o numerador é menor do que o denominador, o que garante que o valor seja menor que 1. Exemplos clássicos são 1/2, 3/5 e 10/11, frações que representam partes menores que o todo. Elas aparecem muito em situações de “parte consumida”, “parte do caminho percorrido”, “porção de alunos”, etc.

Já as frações impróprias são aquelas cujo numerador é maior ou igual ao denominador, o que faz com que o valor seja maior ou igual a 1. Nessa categoria entram exemplos como 7/4, 5/3 e 11/3. Em muitos problemas, faz sentido converter essas frações em números mistos (1 3/4, 2 2/3, etc.), principalmente quando trabalhamos com medidas de comprimento, massa ou tempo.

Existe ainda a chamada fração aparente, que, apesar de estar escrita com numerador e denominador, representa na verdade um número inteiro. Isso acontece, por exemplo, em 8/4 = 2, 5/5 = 1 e 12/3 = 4. Em vários problemas práticos, ao simplificar, você cairá em frações aparentes que deixam a conta bem mais simples.

Finalmente, chamamos de fração irredutível aquela que não pode mais ser simplificada, porque não há divisor comum entre numerador e denominador além de 1. Se você tem 8/12, por exemplo, ainda pode simplificar dividindo numerador e denominador por 4, chegando a 2/3. Nesse ponto, 2 e 3 não têm divisores comuns, então 2/3 é irredutível e é assim que a resposta deve aparecer na maior parte das questões de múltipla escolha.

Problemas contextualizados com frações: exemplos resolvidos

Uma maneira muito eficiente de aprender a lidar com frações é observar como elas aparecem em situações do cotidiano. A seguir, veja uma seleção de problemas típicos, com resolução detalhada, que envolvem contagem de acertos, capacidade de reservatórios, salários, herança, pesquisa eleitoral e muito mais.

Em um treino de vôlei, Mariana fez 50 saques e acertou o alvo desejado em 35 deles. A fração que traduz o desempenho dela é dada pelos acertos no numerador e pelo total de saques no denominador, isto é, 35/50. Para analisar melhor a performance, simplificamos: dividindo numerador e denominador por 5, temos 7/10. Isso indica que ela acertou 7 em cada 10 saques, ou 70% do total.

Considere agora um reservatório de 18 000 litros, em que 3/5 da capacidade se encontra preenchida com água. Restam, portanto, 2/5 da capacidade vazia. Para saber o volume que ainda cabe, calcula-se 2/5 de 18 000: multiplicando 2 por 18 000 e dividindo o resultado por 5, obtemos 36 000/5 = 7 200 litros. Logo, ainda é possível colocar 7 200 litros naquele reservatório.

Suponha que, em uma escola, 2/9 dos alunos estejam em recuperação e esse grupo corresponda a 144 estudantes. Dividindo 144 por 2, obtemos 72, que representa 1/9 do total de alunos. Para chegar ao número total, multiplicamos 72 por 9, chegando a 648 estudantes frequentes nessa escola.

Imagine que Kárita distribuiu seu salário da seguinte forma: 1/4 para o aluguel, 1/6 para o supermercado e 1/5 para contas de energia, água e internet. A primeira etapa é somar essas partes para descobrir quanto do salário já foi gasto. Usando o denominador comum 60, temos 1/4 = 15/60, 1/6 = 10/60 e 1/5 = 12/60, o que resulta em 15/60 + 10/60 + 12/60 = 37/60. Isso significa que 37 partes, de um total de 60, foram gastas. Logo, o que sobrou corresponde a 60/60 – 37/60 = 23/60 do salário.

Em um problema de herança, três irmãos — Arnaldo, Aroldo e Afonso — recebem, respectivamente, 1/4, 2/7 e 3/11 do patrimônio, e o restante fica com a mãe. Para saber quem ficou com a maior e a menor parte, é prático transformar cada fração em número decimal: 1/4 = 0,25; 2/7 ≈ 0,28; 3/11 ≈ 0,27. Comparando, vemos que a menor parte é a de Arnaldo (0,25) e a maior é a de Aroldo (aproximadamente 0,28).

Questões de sala de aula também aparecem com frequência. Se em uma turma há 27 alunos e 2/3 deles não usam óculos de grau, então 1/3 usa. Calculando 1/3 de 27, dividimos 27 por 3 e obtemos 9 estudantes que utilizam óculos. Notar a relação entre a fração que representa quem utiliza e quem não utiliza é essencial para montar a conta correta.

Razões entre grupos são frequentemente traduzidas como frações. Em certa sala com 28 meninas e 16 meninos, a fração que expressa a razão entre o número de meninos e o de meninas é 16/28, pois meninos vão no numerador e meninas no denominador. Essa fração pode ser simplificada dividindo ambos os termos por 4, chegando a 4/7, o que indica que, para cada 7 meninas, há 4 meninos.

Também é comum aparecerem problemas em formato de pesquisa eleitoral. Imagine que, em uma escola, uma pesquisa indicou que 2/5 dos alunos votariam no candidato A, metade deles (1/2) votaria em B e os 34 restantes votariam nulo ou em branco. Se x é o total de estudantes, então a quantidade de votos brancos e nulos pode ser vista como x – 2/5 x – 1/2 x. Somando as frações 2/5 e 1/2 (usando denominador 10), temos 4/10 + 5/10 = 9/10, de forma que a parte restante é 1/10 de x. Assim, 1/10 x = 34, o que implica x = 34 × 10 = 340 estudantes.

Frações em receitas, consumo, tempo e proporções

Uma área em que frações aparecem muito de forma natural é na cozinha, em receitas e medidas de ingredientes. Por exemplo, se uma receita pede 1 xícara de açúcar e já foram usados 3/4 de xícara, a pergunta “quanto falta?” é respondida calculando 1 – 3/4. Como 1 pode ser escrito como 4/4, a conta fica 4/4 – 3/4 = 1/4 de xícara ainda faltando.

Leitura de livros e porcentagem concluída de tarefas também costumam ser representadas por frações. Se alguém leu 2/5 de um livro em um dia e mais 1/5 no dia seguinte, a parte lida é 2/5 + 1/5 = 3/5 do livro. De maneira semelhante, se um tanque está com 5/8 da capacidade cheia e se retiram 1/4 (que é equivalente a 2/8), a nova fração de volume no tanque é 5/8 – 2/8 = 3/8.

Em competições, esportes e jogos, as frações medem desempenho, quantidade de provas concluídas ou partidas vencidas. Se um competidor de xadrez ganhou 3/4 das partidas e disputou 16 jogos, o número de vitórias é dado por 3/4 de 16. Multiplicando, temos (3 × 16)/4 = 48/4 = 12 partidas vencidas. Já em um campeonato em que uma equipe completou 2/5 das provas no primeiro dia e 1/5 no segundo, o total de provas já realizadas é 3/5, e ainda falta 1 – 3/5 = 2/5 para terminar.

Frações também são ótimas para modelar gastos de dinheiro. Imagine alguém que gastou 5/6 do valor que possuía e ficou com R$ 20, isto é, com 1/6 do total. Se 1/6 corresponde a 20, basta multiplicar por 6 para encontrar o valor inicial: 20 × 6 = 120. Nesse tipo de problema, a parte que sobra é tão importante quanto a parte que foi gasta.

Outra situação corriqueira envolve consumo de alimentos ou bebidas ao longo do tempo. Se uma pessoa compra 3 litros de leite e usa 1/2 litro em um bolo e mais 1/4 litro em um café, o total consumido é 1/2 + 1/4 = 3/4 de litro. Escrevendo tudo com denominador 4, temos 3 = 12/4 e a conta fica 12/4 – 2/4 – 1/4 = 9/4 litros restantes, que equivalem a 2 1/4 litros.

Em plantação ou produção agrícola, frações medem o que já foi colhido e o que falta colher. Se um agricultor colheu 2/3 de uma produção de milho pela manhã e colheu o resto à tarde, e o total de sacas é 90, então a parte colhida à tarde é 1/3 do total, já que 1 – 2/3 = 1/3. Multiplicando 1/3 por 90, obtemos 30 sacas colhidas no período da tarde.

Frações em questões de vestibular e Enem

Frações aparecem com força em provas de vestibulares e no Enem, quase sempre misturadas com interpretação de texto e contextos reais. A seguir, veja algumas estruturas de questões bem típicas, para perceber como o conteúdo é cobrado.

Uma situação comum é aquela em que o capital de uma empresa é dividido em partes proporcionais entre sócios. Suponha que três sócios tenham participações proporcionais a 4, 6 e 6, e que um deles deseje adquirir uma fração do capital dos outros para igualar os percentuais. Nesse tipo de problema, você normalmente escreve a participação como frações do total (4/16, 6/16 e 6/16, por exemplo), monta equações para igualar essas parcelas e descobre qual fração do capital de cada um precisa ser transferida.

Outra estrutura famosa é o jogo de cartas com frações, em que o jogador precisa ordenar as frações em ordem crescente ou decrescente. Imagine cartas com 3/5, 1/4, 2/3 e 5/9. Uma forma de comparar é transformar cada fração em número decimal: 3/5 = 0,6; 1/4 = 0,25; 2/3 ≈ 0,66; 5/9 ≈ 0,55. Comparando esses valores, chegamos à ordem 1/4 < 5/9 < 3/5 < 2/3, que é a sequência correta crescente.

Questões envolvendo receitas de suco ou mistura de ingredientes também são clássicas. Por exemplo, um suco é preparado com 2/3 de polpa de morango e 1/3 de polpa de acerola, usando embalagens de igual volume. Se o preço da polpa de acerola aumenta e o comerciante quer manter o preço final do suco, ele pode negociar uma redução no valor da polpa de morango. Para resolver, calcula-se o custo do suco antes e depois do reajuste, trabalhando com as frações 2/3 e 1/3 sobre os preços das respectivas polpas, até encontrar quanto o valor da embalagem de morango precisa diminuir.

Em contextos ambientais, como o Pantanal, frações representam a parte de uma região que fica alagada em determinada época. Se a área total é de 140 mil km² e as cheias cobrem até 2/3 dessa área, o cálculo é simples: 2/3 de 140 000. Multiplicamos 2 por 140 000 (280 000) e dividimos por 3, chegando a aproximadamente 93 333 km², valor que costuma aparecer arredondado nas alternativas.

Provas também adoram misturar frações com distâncias, capacidades de tanques e autonomia de veículos. Por exemplo, se um carro tem tanque de 50 L e faz em média 15 km/L, quando o marcador está em certa fração do tanque, pode-se calcular quantos quilômetros ainda podem ser percorridos. Multiplica-se a fração do tanque disponível pelo volume total e, em seguida, esse volume pelo rendimento em km/L. A ideia é escolher, entre postos de combustível ao longo de uma estrada, qual é o mais distante que ainda está ao alcance sem ficar sem gasolina.

Há também problemas sobre perda ou ganho de frações de comprimento de um tecido após lavagem

Se uma peça perde 1/10 de seu comprimento e passa a medir 36 metros, isso quer dizer que ela agora representa 9/10 do tamanho original. Assim, se chamarmos o comprimento inicial de L, temos 9/10 L = 36. Multiplicando ambos os lados por 10/9, obtemos L = 36 × 10/9 = 40 metros antes da lavagem.

Em questões de estrada, frações indicam a parte já concluída de um trajeto e o complemento numérico representa o trecho restante. Imagine que uma empreiteira pavimente 2/5 de uma estrada, enquanto a outra é responsável pelo restante, que corresponde a 81 km. Como o trecho que sobra é 3/5 da estrada (1 – 2/5 = 3/5), temos que 3/5 da extensão total vale 81 km. Assim, o comprimento total é (81 × 5)/3 = 135 km.

Problemas envolvendo divisão de prêmios ou quantias de dinheiro em frações também são bastante recorrentes. Se 20 colegas contribuem com R$ 30 cada, o montante arrecadado é 20 × 30 = 600 reais. Quando o regulamento de uma aposta diz que o primeiro colocado leva 1/2, o segundo 1/3 e o terceiro o restante, calculamos 1/2 de 600 (300 reais), 1/3 de 600 (200 reais) e a parte final, que é 600 – 300 – 200 = 100 reais. As frações precisam somar 1 (ou 100%); caso contrário, há algo incoerente no enunciado.

Na mesma linha, aparecem situações de consumo de pizza ou chocolate em que cada pessoa come uma fração do total. Se uma pizza é dividida em 20 pedaços, e uma pessoa consome 3/12 do total da pizza (fração que pode ser simplificada) e outra 2/5, é necessário converter tudo para a mesma base, calcular quantos pedaços efetivamente foram comidos e, por fim, saber quantos sobraram para outros participantes. Em geral, vale a pena simplificar as frações logo no início para evitar contas desnecessariamente grandes.

Exercícios de múltipla escolha com frações

Além dos exemplos resolvidos passo a passo, é fundamental treinar com questões de múltipla escolha, já que esse é o formato mais comum em provas grandes. A seguir, alguns modelos de enunciados que envolvem distâncias, barras de chocolate, jarras, voltas em autódromo, jogos, sorvetes e frações geradoras de dízimas.

Em um parque, árvores estão igualmente espaçadas entre os pontos A e B, e a figura sugere que a distância entre a primeira e a segunda árvore corresponde a uma certa fração do percurso total. Nesses casos, a estratégia é contar quantos intervalos iguais existem entre A e B e então perceber que cada espaço entre árvores representa 1 sobre esse total. Se houver, por exemplo, 5 intervalos, a distância é de 1/5 do total.

Outro tipo clássico aparece com barras de chocolate divididas em quadradinhos iguais. Se a barra tem, digamos, 18 quadradinhos e a pergunta é quantos precisam ser comidos para consumir 5/6 da barra, basta calcular 5/6 de 18. Multiplica-se 5 por 18 (90) e divide-se por 6, chegando a 15 quadradinhos, se essa for a estrutura da questão. O segredo é sempre relacionar a fração ao número total de partes da barra.

Também é comum ver jarras de refresco e copos medidos em mililitros. Imagine uma jarra de 500 mL preenchida com 3/4 de suco, o que significa 375 mL. Se o líquido é distribuído em copos de 50 mL, preenchendo 2/4 da capacidade de cada um, você calcula quanto foi servido e subtrai do que havia originalmente, encontrando a fração que ainda sobra na jarra. Esse tipo de questão mistura fração com unidades de medida e exige atenção aos valores absolutos.

Competições de corrida trazem problemas em que o competidor abandona a prova após completar certa fração de voltas. Em uma corrida de 56 voltas, se o piloto estava em 2/7 de prova quando sofreu um acidente, o número da volta é dado por 2/7 de 56, que resulta em (2 × 56)/7 = 112/7 = 16. Nesse caso, ele foi retirado na 16ª volta, o que costuma ser uma das alternativas apresentadas.

Há ainda exercícios sobre frações que geram dízimas periódicas, em que você precisa determinar a fração que origina um decimal infinito como 2,54646…. A técnica envolve separar a parte inteira, transformar a parte decimal repetitiva em fração por meio de equações com potências de 10 (por exemplo, 100x e 10x) e então simplificar. No fim, você escolhe, dentre as alternativas, a fração que corresponde ao decimal apresentado.

Com tanta variedade de contextos — esporte, alimentação, finanças, meio ambiente, trânsito, receitas —, fica claro que problemas com frações não são apenas um conteúdo isolado da Matemática. Eles atravessam o currículo inteiro e aparecem “camuflados” em situações reais, o que torna essencial compreender tanto o lado operacional (as contas) quanto o lado interpretativo (o texto do problema).

Quando você domina as operações básicas, reconhece os tipos de frações e se acostuma a traduzir enunciados em expressões numéricas, problemas com frações passam a ser mais previsíveis e até agradáveis de resolver. Com prática em exercícios variados — como os vistos aqui, envolvendo saques, salários, heranças, pesquisas eleitorais, corridas, sorvetes e jarras de refresco —, fica muito mais simples encarar qualquer questão que envolva partes de um todo em provas e no dia a dia, ganhando confiança para avançar em conteúdos mais avançados da Matemática.