A dilatação linear é um fenômeno físico que ocorre quando um material sofre variação em seu comprimento devido ao aumento ou diminuição da temperatura. Essa variação é chamada de dilatação térmica e pode ser calculada por meio de uma fórmula específica, que leva em consideração o coeficiente de dilatação linear do material.
A fórmula para calcular a dilatação linear ((Delta L)) de um material é dada por:
[
Delta L = L cdot alpha cdot Delta T
]
Onde:
– (Delta L) é a variação no comprimento do material;
– (L) é o comprimento inicial do material;
– (alpha) é o coeficiente de dilatação linear do material;
– (Delta T) é a variação de temperatura.
Um exemplo prático de dilatação linear pode ser observado em trilhos de trem. Quando a temperatura aumenta, os trilhos se expandem devido à dilatação térmica, e quando a temperatura diminui, os trilhos se contraem. Essa variação de comprimento dos trilhos é essencial para garantir a segurança e estabilidade das vias férreas.
Conheça exemplos de dilatação linear e entenda seu conceito e aplicações práticas.
A dilatação linear é um fenômeno físico que ocorre quando um material sofre variação em seu comprimento devido à variação da temperatura. Esse tipo de dilatação é bastante comum e pode ser observado em diversas situações do dia a dia.
A fórmula geral para calcular a dilatação linear de um material é:
ΔL = α . L . ΔT
Onde:
ΔL é a variação no comprimento do material,
α é o coeficiente de dilatação linear do material,
L é o comprimento inicial do material, e
ΔT é a variação de temperatura.
Um exemplo prático de dilatação linear é o caso de uma barra metálica de 1 metro de comprimento que sofre uma variação de temperatura de 50°C. Se o coeficiente de dilatação linear do material for de 0,000012/°C, podemos calcular a variação no comprimento da seguinte forma:
ΔL = 0,000012 . 1 . 50 = 0,0006 metros
Portanto, a barra metálica terá uma variação de comprimento de 0,0006 metros, ou seja, 0,6 milímetros.
As aplicações práticas da dilatação linear são diversas, sendo comumente utilizada em engenharia civil, na construção de pontes, viadutos e estruturas metálicas. Também é importante considerar a dilatação térmica em projetos de engenharia mecânica, evitando problemas de encaixe e funcionamento de componentes.
Fórmulas para calcular a dilatação dos corpos em diferentes materiais e situações.
A dilatação linear é um fenômeno físico que ocorre quando um corpo sofre uma variação em suas dimensões devido a mudanças na temperatura. Para calcular a dilatação dos corpos em diferentes materiais e situações, utilizamos algumas fórmulas específicas.
A fórmula geral para calcular a dilatação linear de um corpo é:
ΔL = α * L0 * ΔT
Onde:
ΔL = variação no comprimento do corpo
α = coeficiente de dilatação linear do material
L0 = comprimento inicial do corpo
ΔT = variação na temperatura
O coeficiente de dilatação linear (α) é uma constante que depende do material do corpo e é expresso em 1/°C. Cada material possui um valor específico para o coeficiente de dilatação linear.
Um exemplo prático de cálculo de dilatação linear é o seguinte:
Um trilho de trem de aço, com comprimento inicial de 100m, sofre uma variação de temperatura de 50°C. O coeficiente de dilatação linear do aço é de 11×10^-6 °C^-1. Qual será a variação no comprimento do trilho?
Aplicando a fórmula da dilatação linear, temos:
ΔL = 11×10^-6 * 100 * 50
ΔL = 0,055m
Portanto, a variação no comprimento do trilho será de 0,055m.
Exemplos de dilatação térmica: descubra como materiais se expandem com o calor.
A dilatação térmica é um fenômeno físico que ocorre quando um material se expande devido ao aumento de temperatura. Esse processo é bastante comum e pode ser observado em diversos materiais do nosso dia a dia. Um exemplo clássico de dilatação térmica é o aumento no comprimento de uma barra metálica quando aquecida.
Quando um material é aquecido, as partículas que o compõem ganham energia e passam a vibrar com mais intensidade. Isso faz com que as distâncias entre as partículas aumentem, resultando na expansão do material. Esse fenômeno é conhecido como dilatação térmica.
Um exemplo prático de dilatação térmica linear é a dilatação de trilhos de trem em dias muito quentes. Quando expostos ao sol, os trilhos se expandem devido ao calor, o que pode causar problemas na estrutura da linha férrea.
A fórmula matemática que descreve a dilatação linear de um material é: ΔL = L0 * α * ΔT, onde ΔL é a variação no comprimento, L0 é o comprimento inicial, α é o coeficiente de dilatação linear do material e ΔT é a variação de temperatura.
Os coeficientes de dilatação linear variam de acordo com o material. Por exemplo, o coeficiente de dilatação do aço é de aproximadamente 12×10^-6 1/°C, enquanto o do alumínio é de aproximadamente 23×10^-6 1/°C.
Em resumo, a dilatação térmica é um fenômeno natural que ocorre devido ao aumento de temperatura. Entender como os materiais se expandem com o calor é essencial para diversos campos da ciência e da engenharia.
Três tipos de dilatação: quais são e como se manifestam em materiais diferentes.
A dilatação é um fenômeno físico que ocorre quando um material se expande devido ao aumento de temperatura. Existem três tipos de dilatação: linear, superficial e volumétrica. Cada tipo se manifesta de forma diferente em materiais diversos, de acordo com suas características físicas.
A dilatação linear ocorre em um único sentido, ou seja, em uma única dimensão. Ela é mais comum em materiais como barras metálicas, fios e cabos. A fórmula para calcular a dilatação linear é:
ΔL = α * L * ΔT
Onde ΔL representa a variação do comprimento, α é o coeficiente de dilatação linear do material, L é o comprimento inicial e ΔT é a variação de temperatura. Um exemplo prático de dilatação linear é quando um trilho de trem se expande em dias quentes, causando problemas na circulação dos trens.
Os coeficientes de dilatação linear variam de acordo com o material. Materiais como o aço apresentam um coeficiente de dilatação linear maior do que materiais como o vidro, o que os torna mais propensos a se expandir com o aumento de temperatura.
Em resumo, a dilatação linear é um fenômeno físico que ocorre em materiais como barras metálicas, fios e cabos, e pode ser calculada utilizando a fórmula ΔL = α * L * ΔT. Os coeficientes de dilatação linear variam de acordo com o material, influenciando na forma como cada material se expande com o aumento de temperatura.
Dilatação linear: o que é, fórmula e coeficientes, exemplo
A expansão linear ocorre quando um objecto submetido a expansão, devido a uma variação de temperatura, predominantemente numa dimensão. Isso se deve às características do material ou à sua forma geométrica.
Por exemplo, em um fio ou em uma barra, quando há um aumento de temperatura, é o comprimento que sofre a maior mudança devido à expansão térmica.

Os cabos nos quais os pássaros da figura anterior pousam sofrem um estiramento quando a temperatura aumenta; em vez disso, eles se contraem quando esfriam.Da mesma forma, acontece, por exemplo, com as barras que formam os trilhos de uma ferrovia.
O que é dilatação linear?
Em um material sólido, os átomos mantêm suas posições relativas mais ou menos fixadas em torno de um ponto de equilíbrio. No entanto, devido à agitação térmica, eles estão sempre girando em torno dele.
À medida que a temperatura aumenta, a oscilação térmica também aumenta, fazendo com que as posições médias de oscilação mudem. Isso ocorre porque o potencial de ligação não é exatamente parabólico e tem assimetria em torno do mínimo.
Abaixo está uma figura que descreve a energia da ligação química em função da distância interatômica. Também mostra a energia total de oscilação a duas temperaturas e como o centro da oscilação se move.

Fórmula de expansão linear e seu coeficiente
Para medir a expansão linear, começamos com um comprimento inicial L e uma temperatura inicial T, do objeto do qual você deseja medir sua expansão.
Suponha que o objeto seja uma barra cujo comprimento seja L e as dimensões da seção transversal sejam muito menores que L.
Primeiro, o referido objeto é sujeito a uma variação de temperatura AT, de modo que a temperatura final do objeto, uma vez estabelecido o equilíbrio térmico com a fonte de calor, seja T ‘= T + AT.
Durante esse processo, o comprimento do objeto também será alterado para um novo valor L ‘= L + ΔL, onde ΔL é a variação no comprimento.
O coeficiente de expansão linear α é definido como a razão entre a variação relativa no comprimento por unidade de variação de temperatura.A fórmula a seguir define o coeficiente de expansão linear α :

As dimensões do coeficiente de expansão linear são as do inverso da temperatura.
Coeficiente de expansão linear para vários materiais
Abaixo, listaremos o coeficiente de expansão linear para alguns materiais e elementos típicos. O coeficiente é calculado à pressão atmosférica normal, com base em uma temperatura ambiente de 25 ° C; e seu valor é considerado constante em uma faixa de ΔT de até 100 ° C.
A unidade do coeficiente de expansão linear será (° C) -1 .
– Aço: α = 12 ∙ 10 -6 (° C) -1
– Alumínio: α = 23 ∙ 10 -6 (° C) -1
– Ouro: α = 14 ∙ 10 -6 (° C) -1
– Cobre: α = 17 ∙ 10 -6 (° C) -1
– Latão: α = 18 ∙ 10 -6 (° C) -1
– Ferro: α = 12 ∙ 10 -6 (° C) -1
– Vidro: α = (7 a 9) ∙ 10 -6 (° C) -1
– Mercúrio: α = 60,4 ± 10 -6 (° C) -1
– Quartzo: α = 0,4 ± 10 -6 (° C) -1
– Diamante: α = 1,2 ∙ 10 -6 (° C) -1
– Chumbo: α = 30 ∙ 10 -6 (° C) -1
– Madeira de carvalho: α = 54 ∙ 10 -6 (° C) -1
– PVC: α = 52 × 10 -6 (° C) -1
– Fibra de carbono: α = -0,8 ± 10 -6 (° C) -1
– Concreto: α = (8 a 12) ∙ 10 -6 (° C) -1
A maioria dos materiais estica com um aumento de temperatura. No entanto, alguns materiais especiais, como fibra de carbono, encolhem com o aumento da temperatura.
Exemplos resolvidos de expansão linear
Exemplo 1
Um fio de cobre é pendurado entre dois postes, e seu comprimento em um dia frio a 20 ° C é de 12 m. Calcular o valor da sua duração em um dia quente a 35 ° C.
Solução
Partindo da definição do coeficiente de expansão linear e sabendo que para o cobre esse coeficiente é válido: α = 17 ∙ 10 -6 (° C) -1

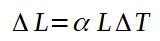
O fio de cobre sofre um aumento no seu comprimento, mas isso é de apenas 3 mm. Ou seja, o cabo passa de 12.000 ma 12.003 m.
Exemplo 2
Na indústria siderúrgica, uma barra de alumínio sai do forno a 800 graus Celsius, medindo um comprimento de 10,00 m. Quando esfriar até a temperatura ambiente de 18 graus Celsius, determine quanto tempo a barra será.
Solução

Ou seja, a barra, uma vez fria, terá um comprimento total de:
9,83 m.
Exemplo 3
Um rebite de aço tem um diâmetro de 0,915 cm. Uma folga de 0,910 cm é feita em uma placa de alumínio. Estes são os diâmetros iniciais quando a temperatura ambiente é de 18 ° C.
A que temperatura mínima a placa deve ser aquecida para que o rebite passe pelo orifício? O objetivo é que, quando o ferro retorna à temperatura ambiente, o rebite é ajustado na chapa.

Solução
Embora a placa seja uma superfície, estamos interessados em dilatar o diâmetro do furo, que é uma quantidade unidimensional.
Vamos chamar D 0 do diâmetro original da placa de alumínio e D que ela terá aquecido uma vez.
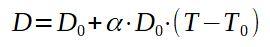
Limpando a temperatura final T, você tem:

O resultado das operações anteriores é de 257 ° C, que é a temperatura mínima na qual a placa deve ser aquecida para que o rebite passe pelo orifício.
Exemplo 4
O rebite e o prato do exercício anterior são colocados juntos no forno. Determine a que temperatura mínima o forno deve estar para que o rebite de aço passe pelo orifício na placa de alumínio.
Solução
Nesse caso, o rebite e o furo serão expandidos. Mas o coeficiente de expansão do aço é α = 12 ∙ 10 -6 (° C) -1 , enquanto o do alumínio é α = 23 ∙ 10 -6 (° C) -1 .
Em seguida, procuramos uma temperatura final T tal que os dois diâmetros correspondam.
Se chamamos 1 de rebite e 2 de chapa de alumínio, procuramos uma temperatura final T tal que D 1 = D 2 .

Se limparmos a temperatura final T, temos:
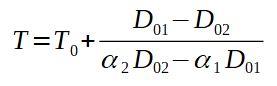
Em seguida, colocamos os valores correspondentes.

A conclusão é que o forno deve ter pelo menos 520,5 ° C para que o rebite passe pelo orifício na placa de alumínio.
Referências
- Giancoli, D. 2006. Física: Princípios com Aplicações. Sexta Edição Prentice Hall. 238-249.
- Bauer, W. 2011. Física para Engenharia e Ciência. Volume 1. Mac Graw Hill. 422-527.